
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
IV. A CONCEPT SELECTION PROCESS
The concept selection process presented here is a means to deal with this uncertainty. The process is designed to be a daylong out-of-the-office exercise, where a design team evaluates alternatives and comes to a consensus on the most effective concept to pursue. The process is focused on clearly articulating differences in understanding among team members, forming common definitions, and expanding the options considered that are due to these differences in understanding. When the process is implemented, as described, a design team will have agreement on the concept to pursue, every engineer on the team will understand why they changed their mind to the collective consensus, and finally, every engineer will be supportive of their change in position.
Failing this state of consensus, the team will understand exactly why there remains a difference in opinion and be in agreement on what must be further analyzed to resolve the issue. In such a case, the concept selection will then be completely determined by the results of this one analysis.
The concept selection process should be completed in a room with at least three walls that can be written on, paper attached to, or overhead projectors shown on. One wall will have definitions of criteria and alternatives displayed, another wall will be a working wall with the evaluation interaction, and a final wall will be used to keep notes and rejected information.
The selection process is a five-step process plus iterations:
1. Forming consensus on the criteria,
2. Forming consensus on the alternatives,
3. Ranking the alternatives,
4. Evaluating the alternatives,
5. Attacking the negatives.
Earlier steps are revisited during the latter steps as needed for refinement, and the steps themselves are repeated in several sequences.
V. A BASIC METHOD: PUGH CONCEPT SELECTION CHARTS
http://www.youtube.com/watch?v=FD9Y3GMwofI
http://www.youtube.com/watch?v=5DeDXsGvA_w
The above process can be applied with decision-making tools as developed by Pugh (1990). These tools, known as Pugh charts, use a minimal evaluation scale and three overall ranking metrics. Pugh charts are the most effective known tools for preliminary concept selection when there is minimal information quality available. They are also effective as the information quality increases and the selection scale is refined. The goal of any selection process is to obtain as much information and concept details as cycle time and resources permit.
Establish the Criteria and Alternatives
With Pugh selection charts, the criteria and concept alternatives are established as discussed above. The ranking procedure, however, takes a particular form. The alternatives and criteria are displayed on the main wall labeled Pugh Selection Chart, as outlined in Figure 11.2. Here, the concept sketches are displayed at the top of the matrix as columns. Each criterion is listed down each row.
Select a Datum
The next step is to establish the evaluation scale. Pugh (1990) correctly advocated using a minimal scale of only {-, s, +} for evaluating preliminary concepts. Further refinement of the scale, such as with numerical rankings and/or numerical weights, may not be feasible at the preliminary concept selection phase. A team may not be able to supply such detailed ranks for some criteria, and so the evaluation is error prone, where incomplete rough ratings combined with good ratings can numerically alter the result.
Rather, an effective process is to construct a simple evaluation scale (unless more information is known). To do this, the team should select one alternative that will be ranked as (s) (or 0) on every criterion and be called the datum. The datum is the alternative to which every other concept will be compared. The other concepts are rated as either worse ( - ), the same (s ), or better ( + ), on each criterion.

To select a datum, a team can choose one of several approaches. The current product offered by the company might serve as a well understood concept. A competitive product that a team wishes to surpass might serve as a datum.
Pugh (1990) recommends using the alternative that the team votes as best (or preferred) as the datum. That is, the team members vote on each alternative, and the alternative with the majority of the votes serves as the datum. This choice accomplishes two things. First, the distribution of disagreement is understood. Second, since the team-chosen alternative is likely to be carried into the next round of comparisons after attacking the negatives, it ought to be used as the preferred datum. The choice of a datum should not shift from round to round of rankings (e.g., if every alternative advanced to the second round has (+) ranks relative to the existing product).
Example: Coffee Mill
http://www.youtube.com/watch?v=AaHoATwopqY
As an example, consider the redesign of a coffee mill, restricted to using a chopper concept. Several ideas are developed to improve the mill, focusing on the evolution of the cleaning functions of the mill. These ideas are shown in Table 11.2. A Pugh concept selection process is undertaken to resolve these concepts into one to pursue development. Each of these concepts is depicted on 8.5" x 11" sheets of paper and posted on a wall as columns. Discussion is facilitated to elaborate on the positives and difficulties of each concept. These difficulties are recorded as notes under each concept in Table 11.2. Refined sketches are also developed to clarify issues raised during the discussion.
Next, the evaluation criteria are elaborated, as shown in Table 11.3. These criteria arise directly from the customer needs and engineering specifications previously developed for the product. Again, factors elaborated about each criterion are shown in the table. Having completed this process, the next step entails the implementation of the Pugh selection process. The results of the concept ranking are shown in Table 11.4.
Some observations are apparent when completing this first round of the selection process. First, the power set-up criterion did not distinguish or discriminate between the concepts. They were all about the same. Therefore, although it is an important criterion for the product, the different concepts for promoting cleanability do not impact it. Therefore, it is dropped from further discussion.
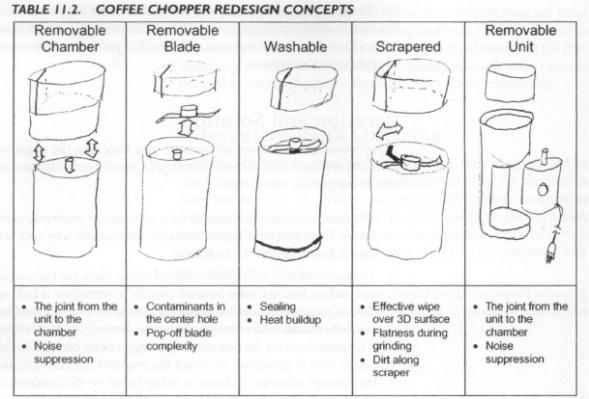

Next, it appears that the decision is reduced to the removable blade concept, and any ideas the team may have to convert any of the other concepts such that their negatives go away. So, each concept to be dropped is scrutinized. A suggestion is made to use a small electric plug at the base of the mill to permit it to be removed from the cord. Then the mill itself is as portable as a removable chamber and would make the scraper concept have a 0 rank on the "pour coffee out" criterion. This modification is then a new concept that competes effectively with the removable blade concept. And so on.

http://vimeo.com/109020599
VI. ADVANCED DISCUSSION: MEASUREMENT THEORY
The Pugh chart selection process is effective, but there are many other methods available for design decision making. Numerical rankings, weighted sums, utility theory, probability theory, and fuzzy sets, for example, have all been advocated for different decision-making tasks.
One means to understanding these different methods is to examine the information quality used in the scores applied to each alternative. The basic Pugh process uses a very simple scale: better, worse, or the same. One might instead apply thoughts of "twice as good," or "half as bad," indicating ranks of 2 and -~, respectively. Measurement theory (Krantz et al.) is an analysis approach to establish, for example, when this refinement in the selection scale can and cannot be done.
There are several levels of information quality to measure alternatives on different criteria. Information quality can be more formally considered as the level of structure associated with the alternatives and the criteria used.
Ordinal Scales
Having a set of product options is not sufficient to make a decision. A "best" or most preferred option must be identified: An evaluation structure must be constructed. The simplest structure is to assign each option a label of "equal or better" or "equal or worse."
Any reasoning on which a product design can be judged forms an evaluation criterion, Φ for rating designs. The label Φ is not to signify that a criterion is a numerical function; rather Φ is merely a label. The existence of at least one such reason is the second axiomatic assumption required to form an evaluation.
The Better/Worse Method
One evaluation procedure commonly used is the better/worse method. First we select an arbitrary alternative from X to form the beginning of a list {xo} indexed by j. For every other alternative, we start at the bottom of the list and move up through the list, asking

Once xi is no longer better than xj we then insert xi into the list at that point. The set S of possible ranks for any evaluation is:

The line of questioning (Ql) interactively produces a bubble sort of the alternatives. The best or most preferred alternative is at the head of the list, and the evaluation among the alternatives is complete.
Pro/Con Charts
http://www.youtube.com/watch?v=yimDWPyQpkY
https://www.youtube.com/watch?v=oh03fuIlQNI
https://www.youtube.com/watch?v=VeWayRm0cmU
A Pro/Con chart is a minimally structured decision-making tool for problems with multiple alternatives xi and multiple criteria Φ. Here, a design team constructs a chart with the alternatives represented by columns. Two rows are then created. In the top row, criteria are entered that an alternative is rated positively on and are considered as "Pro" for the alternative. In the bottom row, the criteria are entered that an alternative is evaluated negatively on and are considered as "Con" for the alternative. Then the design team considers this chart result as one holistic expression. Typically, such a Pro/Con chart is used to help identify one's thoughts succinctly or to agree as a group on a winning alternative.
When a Pro/Con is used as a basis of evaluation, however, it should be understood what underlies the mechanics of the process. The information required and the elemental steps that must be applied should be analyzed. With a Pro/Con chart, the set of alternatives is ranked into the evaluation levels "Pro;' "Con;' or "Neither" for each of the different criteria. These evaluation levels can be identified into a simple set of rank values:
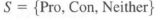
The ordinal question asked on each alternative Xi for each criteria Φj is:

Generally speaking, if Φj is better, then xi gets a "Pro" rating; if worse, then Xi gets a "Con" rating. If it is neither better nor worse, then the criterion Φj remains blank as a "Neither" on xi.
Notice that a difficulty arises in this approach: There is no datum for the ranking. For each criterion, the Pro/Con method attempts to rank each configuration in a general reference frame that does not indicate what either "Pro" or "Con" means. "Pro;' "Con;' or "Neither" as compared to what? Such evaluation without a datum can prove difficult to maintain consistency.
After the ranking is complete for each criterion, the alternatives must still be ordered. Typically, this ordering is completely informal by holistically considering all criteria simultaneously and informally completing the bubble sort using the better/worse method. The original ordinal rank construction question (Ql) is asked not on just one criterion, Φ, but on all of the criteria Φ simultaneously. With a Pro/Con chart, all the criteria must be considered simultaneously when placing each alternative xi in order. One could list the criteria as "Pro" or "Con" and make a qualitative decision based on these rankings as shown in Table 11.5.
Pugh Charts
http://www.youtube.com/watch?v=aS8GYTslcFI
The Pugh chart evaluation scheme presented earlier involves sets of alternatives, sets of criteria, and a better/same/worse evaluation against a datum. We can address the mechanics of the Pugh chart in an objective way.
With the set of alternatives and criteria, there are three basic mathematical tasks that are completed:
l. Identify a datum alternative.
2. Rank every other alternative as better/same/worse for each criterion Φj.
3. Sum the ranks for an overall evaluation of each configuration.
Consider the first task (Step 1). When constructing the chart, an effective process demands that a designer first select an alternative to serve as a datum. In measurement theory, an alternative selected as the zero point for a scale is termed the base point. Its criterion value effectively serves as a "zero" on the measurement of the criteria over the set of alternatives; all others are rated as higher or lower in the criteria.
Having selected a base point (datum), the next task (Step 2) is to rank each alternative in comparison to the datum, using evaluation levels of


This set forms a weak ordering (into three groups) of the alternatives in terms of each criterion Φj. Ordinal scales (X, ≤) have been constructed over the set of alternatives X, one each in terms of the criterion Φj Therefore, Steps 1 and 2 are well grounded in measurement theory. The process results in several mathematically correct weak orders among the alternatives.
The next task in the process is to combine these measured results (Step 3). The procedure is to "add" the rankings as if they were numbers. If the overall rank is used as an objective figure of merit to select a preferred concept, then, mathematically, difficulties will arise. To "add" the rankings, then a distance separation has been assigned to the rank set:

This mapping, Eq. (11.2), must be closely examined. First, it implies that in the overall rating, Sj, every criterion is assigned an impact of ± 1. This impact must mean that a selection based on the final additive sum is in fact based on the net number of criteria that an alternative offers for improvement. If a final result has an alternative ranked at + 3, this means that the alternative is better than the base point by a net of three criteria. This statement is the only interpretation of the final result, whereby the (-, S,+) rank can be evaluated ordinally using the equivalence of Eq. (11.2).
VII. ADVANCED METHOD: NUMERICAL CONCEPT SCORING
The discussion on interval and ratio scales can be applied to complete a numerical concept selection. As an example, consider a material selection problem for a refrigerated food preparation surface material (to be subsequently coated) for use in an ice cream store, where hand mixing of ingredients on the surface is needed.
Date: 2016-01-14; view: 877
| <== previous page | | | next page ==> |
| Information Quality | | | Model Preparation and Selection Method |