Co wyraża i gdzie ma zastosowanie trend liniowy?

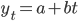
W tej postaci trend jest opisywany przez dwa parametry: a oraz b, nazywające się odpowiednio wyrazem wolnym oraz współczynnikiem kierunkowym. Ze wzoru (a także z własności funkcji liniowej) wynika, że wyraz wolny odpowiedzialny jest za poziom na którym znajduje się linia trendu, a współczynnik kierunkowy odpowiada za kąt nachylenia względem osi wykresu.

Nie zawsze model liniowy dobrze odzwierciedla zmiany w czasie pewnego nadanego zjawiska Jeśli np. sprzedawca wprowadza w śorkachmasowego przekazu silnąkampanię reklamową to tempo sprzedaży jego produktów jest znacznie wieksze niz opisuje to trend liniowy i wtedy stosujemy inne postacie jak na przykład:

a) funkcję wykładniczą o postaci:

Właściwością tej funkcji jest stopa wzrostu wynosząca: [dla modelu pierwszego]

i [dla modelu drugiego];

b) wielomian stopnia drugiego (parabola):

> 0

Zaletą tej funkcji jest jej duża elastyczność, wynikająca z posiadania trzech parametrów. Dzięki temu funkcja ta dobrze sie dopasowuje lepiej odzwierciedlając różne nieliniowe tendencje rozwojowe;

c) potęgową:

> 1.

Funkcja ta przydaje sie zwłaszcza do opisu tendencji rozwojowych, które po logarymowaniu wykazują przebieg liniowy.

Co wyraża średnie roczne tempo wzrostu (stopa wzrostu) i jego znaczenie?

Do czego stosowany jest trend wykładniczy?

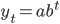
o opisu zjawisk charakteryzujących się systematycznym wzrostem (lub spadkiem) wartości w czasie, można wykorzystać jeszcze (poza funkcją liniową i wielomianową) funkcję wykładniczą.

Postać wykładnicza ma dwa parametry:

t - decyduje o skali zjawiska. Jeśli t>0, uzyskuje się modele symetryczne względem osi OX do przypadku -t; przypadek t=0 jest równoważny wielomianowi stopnia zerowego.

a - decyduje o kierunku rozwoju: dla a>0 jest wzrost wartości, a dla a<0 ze spadkiem wartości.

W porównaniu do poprzednich modeli, w trendzie wykładniczym nie ma parametru bezpośrednio odpowiedzialnego za poziom.

Do czego stosowany jest trend hiperboliczny?

trend hiperboliczny - opisuje zjawisko, kture wykazuje tendencję

spadkową, ale przypuszczamy, że zjawisko to z upływem czasu ustabilizuje się na

pewnym niezerowym poziomie.

Date: 2016-01-14; view: 1138