Give specification of using pre- and post- conditions and formal semantics of operators and selection cycle

Precondition– it is a predicate which defines, at what possible values of entrance variables the program S has to work

The post-condition is a predicate which defines, what values of variables of the program S after its end are correct S

P1 is stronger, than P2 (and P2 is weaker, than P 1), if performance of a condition P1 involves performance conditions P2, but they aren't equivalent formally P1 => P2

For example, P1 condition = {x>2 } is stronger than P2 condition = {x>0 } as when performing P1 both P2, and these conditions is carried out aren't equivalent the

Example: P1 (x) defines a set of squares, P2 (x) – a set of rectangles of

True – the weakest, False – the strongest conditions

The program will transform data, therefore the condition of the program changes. Therefore also statements which were fair prior to the beginning of the program, will change

There is a program S and three predicates:

I – a precondition - a condition which, according to the assumption, is met conditions of S prior to performance of S

R – a post-condition to which have to satisfy conditions of the program S after its end (post-condition)

sp (S, I) – the strongest post-condition to which satisfy program variables after end of S if they satisfied to a precondition of I (it is calculated according to the program and I)

Theorem. The program S is partially correct, iff sp (S, I) =>R

The weakest precondition, weakest precondition: wp (S, R) –predicate to which satisfy all those initial conditions of the program S which will inevitably lead to such final condition of S which will satisfy to the set predicate

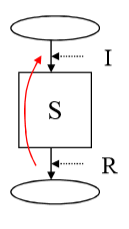I – to this predicate satisfy initial conditions of S

R – to this predicate have to satisfy final conditions of S at its end

Theorem. The program S is partially correct, iff I => wp (S, R)

Selection cycle

Date: 2016-01-03; view: 1092