
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The Michaelis Constant, Km
The ratio of constants (k-1 + k2)/k1 is itself a constant and is defined as the Michaelis constant, Km
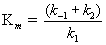 (14.16)
(14.16)
Note from (14.15) that Km is given by the ratio of two concentrations (([ET] - [ES]) and [S]) to one ([ES]), so Km has the units of molarity. From Equation (14.15), we can write
 (14.17)
(14.17)
which rearranges to
 (14.18)
(14.18)
Now, the most important parameter in the kinetics of any reaction is the rate of product formation. This rate is given by
 (14.19)
(14.19)
and for this reaction
v = k2[ES] (14.20)
Substituting the expression for [ES] from Equation (14.18) into (14.20) gives
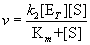 (14.21)
(14.21)
The product k2[ET] has special meaning. When [S] is high enough to saturate all of the enzyme, the velocity of the reaction, v, is maximal. At saturation, the amount of [ES] complex is equal to the total enzyme concentration, ET, its maximum possible value. From Equation (14.20), the initial velocity v then equals k2[ET] = Vmax. Written symbolically, when [S] >> [ET] (and Km), [ET] = [ES] and v = Vmax. Therefore,
Vmax = k2[ET] (14.22)
Substituting this relationship into the expression for v gives the Michaelis-
Menten equation
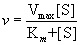 (14.23)
(14.23)
This equation says that the rate of an enzyme-catalyzed reaction, v, at any moment is determined by two constants, Km and Vmax, and the concentration of substrate at that moment.
When [S] = Km, v = Vmax/2
We can provide an operational definition for the constant Km by rearranging Equation (14.23) to give
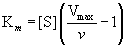 (14.24)
(14.24)
Then, at v = Vmax/2, Km = [S]. That is, Km is defined by the substrate concentration that gives a velocity equal to one-half the maximal velocity. Table 14.3 gives the Km values of some enzymes for their substrates.
| Table 14.3 | ||
| Km Values for Some Enzymes | ||
| Enzyme | Substrate | Km (mM) |
| Carbonic anhydrase | CO2 | |
| Chymotrypsin | N-Benzoyltyrosinamide Acetyl-L -tryptophanamide N-Formyltyrosinamide N-Acetyltyrosinamide Glycyltyrosinamide | 2.5 5 12 32 122 |
| Hexokinase | Glucose Fructose | 0.15 1.5 |
| b-Galactosidase | Lactose | |
| Glutamate dehydrogenase | NH4+ Glutamate α -Ketoglutarate NAD+ NADH | 57 0.12 2 0.025 0.018 |
| Aspartate aminotransferase | Aspartate α -Ketoglutarate Oxaloacetate Glutamate | 0.9 0.1 0.04 4 |
| Threonine deaminase | Threonine | |
| Arginyl-tRNA synthetase | Argininet RNAArg ATP | 0.003 0.0004 0.3 |
| Pyruvate carboxylase | HCO3- Pyruvate ATP | 1.0 0.4 0.06 |
| Penicillinase | Benzylpenicillin | 0.05 |
| Lysozyme | Hexa-N-acetylglucosamine | 0.006 |
Relationships Between Vmax, Km, and Reaction Order
The Michaelis-Menten equation (14.23) describes a curve known from analytical geometry as a rectangular hyperbola.1 In such curves, as [S] is increased, v approaches the limiting value, Vmax, in an asymptotic fashion. Vmax can be approximated experimentally from a substrate saturation curve (Figure 14.7), and Km can be derived from Vmax /2, so the two constants of the Michaelis-Menten equation can be obtained from plots of v versus [S]. Note, however, that actual estimation of Vmax, and consequently Km, is only approximate from such graphs. That is, according to Equation (14.23), in order to get v = 0.99 Vmax, [S] must equal 99 Km, a concentration that may be difficult to achieve in practice.
From Equation (14.23), when [S] >> Km, then v = Vmax. That is, v is no longer dependent on [S], so the reaction is obeying zero-order kinetics. Also, when [S] < Km, then v » (Vmax/ Km)[S]. That is, the rate, v, approximately follows a first-order rate equation, v = k'[A], where k' = Vmax / Km.
Km and Vmax, once known explicitly, define the rate of the enzyme-catalyzed reaction, provided:
1. The reaction involves only one substrate, or if the reaction is multisubstrate, the concentration of only one substrate is varied while the concentration of all other substrates is held constant.
2. The reaction ES ® E + P is irreversible, or the experiment is limited to observing only initial velocities where [P] = 0.
3. [S]0 > [ET] and [ET] is held constant.
4. All other variables that might influence the rate of the reaction (temperature, pH, ionic strength, and so on) are constant.
Enzyme Units
In many situations, the actual molar amount of the enzyme is not known. However, its amount can be expressed in terms of the activity observed. The International Commission on Enzymes defines One International Unit of enzyme as the amount that catalyzes the formation of one micromole of product in one minute. (Because enzymes are very sensitive to factors such as pH, temperature, and ionic strength, the conditions of assay must be specified.) Another definition for units of enzyme activity is the katal. One katal is that amount of enzyme catalyzing the conversion of one mole of substrate to product in one second. Thus, one katal equals 6 x 107 international units.
Turnover Number
The turnover number of an enzyme, kcat, is a measure of its maximal catalytic activity. kcat is defined as the number of substrate molecules converted into product per enzyme molecule per unit time when the enzyme is saturated with substrate. The turnover number is also referred to as the molecular activity of the enzyme. For the simple Michaelis-Menten reaction (14.9) under conditions of initial velocity measurements, k2 = kcat. Provided the concentration of enzyme, [ET], in the reaction mixture is known, kcat can be determined from Vmax. At saturating [S], v = Vmax = k2 [ET]. Thus,
 (14.25)
(14.25)
The term kcat represents the kinetic efficiency of the enzyme. Table 14.4 lists turnover numbers for some representative enzymes. Catalase has the highest turnover number known; each molecule of this enzyme can degrade 40 million molecules of H2O2 in one second! At the other end of the scale, lysozyme requires 2 seconds to cleave a glycosidic bond in its glycan substrate.
| Table 14.4 | |
| Values of kcat (Turnover Number) for Some Enzymes | |
| Enzyme | kcat (sec-1) |
| Catalase | 40,000,000 |
| Carbonic anhydrase | 1,000,000 |
| Acetylcholinesterase | 14,000 |
| Penicillinase | 2,000 |
| Lactate dehydrogenase | 1,000 |
| Chymotrypsin | |
| DNA polymerase I | |
| Lysozyme | 0.5 |
kcat/Km
Under physiological conditions, [S] is seldom saturating, and kcat itself is not particularly informative. That is, the in vivo ratio of [S]/Km usually falls in the range of 0.01 to 1.0, so active sites often are not filled with substrate. Nevertheless, we can derive a meaningful index of the efficiency of Michaelis-Menten-type enzymes under these conditions by employing the following equations. As presented in Equation (14.23), if

and Vmax = kcat [ET], then
 (14.26)
(14.26)
When [S] << Km, the concentration of free enzyme, [E], is approximately equal to [ET], so that
 (14.27)
(14.27)
That is, kcat / Km is an apparent Second-order rate constant for the reaction of E and S to form product. Because Km is inversely proportional to the affinity of the enzyme for its substrate and kcat is directly proportional to the kinetic efficiency of the enzyme, kcat / Km provides an index of the catalytic efficiency of an enzyme operating at substrate concentrations substantially below saturation amounts.
An interesting point emerges if we restrict ourselves to the simple case where kcat = k2. Then
 (14.28)
(14.28)
But k1 must always be greater than or equal to k1k2/(k-1 + k2). That is, the reaction can go no faster than the rate at which E and S come together. Thus, k1 sets the upper limit for kcat / Km. In other words, the catalytic efficiency of an enzyme cannot exceed the diffusion-controlled rate of combination of E and S to form ES. In H2O, the rate constant for such diffusion is approximately 109/M × sec. Those enzymes that are most efficient in their catalysis have kcat / Km ratios approaching this value. Their catalytic velocity is limited only by the rate at which they encounter S; enzymes this efficient have achieved so-called catalytic perfection. All E and S encounters lead to reaction because such “catalytically perfect” enzymes can channel S to the active site, regardless of where S hits E. Table 14.5 lists the kinetic parameters of several enzymes in this category. Note that kcat and Km both show a substantial range of variation in this table, even though their ratio falls around 108/M × sec.
| Table 14.5 | ||||
| Enzymes Whose kcat /Km Approaches the Diffusion-Controlled Rate of Association with Substrate | ||||
| Enzyme | Substrate | kcat (sec-1) | Km (M) | kcat /Km (sec-1 M-1) |
| Acetylcholinesterase | Acetylcholine | 1.4 x 104 | 9 x 10-5 | 1.6 x 108 |
| Carbonic anhydrase | CO2 HCO3- | 1 x 106 4 x 105 | 0.012 0.026 | 8.3 x 107 1.5 x 107 |
| Catalase | H2O2 | 4 x 107 | 1.1 | 4 x 107 |
| Crotonase | Crotonyl-CoA | 5.7 x 103 | 2 x 10-5 | 2.8 x 108 |
| Fumarase | Fumarate Malate | 800 900 | 5 x 10-6 2.5 x 10-5 | 1.6 x 108 3.6 x 107 |
| Triosephosphate isomerase | Glyceraldehyde- 3-phosphate* | 4.3 x 103 | 1.8 x 10-5 | 2.4 x 108 |
| b-Lactamase | Benzylpenicillin | 2 x 103 | 2 x 10-5 | 1 x 108 |
| *Km for glyceraldehyde-3-phosphate is calculated on the basis that only 3.8% of the substrate in solution is unhydrated and therefore reactive with the enzyme. Adapted from Fersht, A. 1985. Enzyme Structure and Mechanism, 2nd ed. New York : W.H. Freeman & Co. |
Date: 2016-01-03; view: 1326
| <== previous page | | | next page ==> |
| Kinetics of Enzyme-Catalyzed Reactions | | | Linear Plots Can Be Derived from the Michaelis - Menten Equation |