Close-packing of identical spheres

Crystals are of course three-dimensional objects, but we will begin by exploring the properties of arrays in two-dimensional space. This will make it easier to develop some of the basic ideas without the added complication of getting you to visualize in 3-D — something that often requires a bit of practice.

Suppose you have a dozen or so marbles. How can you arrange them in a single compact layer on a table top? Obviously, they must be in contact with each other in order to minimize the area they cover. It turns out that there are two efficient ways of achieving this:

The essential difference here is that any marble within the interior of the square-packed array is in contact with four other marbles, while this number rises to six in the hexagonal-packed arrangement. It should also be apparent that the latter scheme covers a smaller area (contains less empty space) and is therefore a more efficient packing arrangement.

If you are good at geometry, you can show that square packing covers 78 percent of the area, while hexagonal packing yields 91 percent coverage.

If we go from the world of marbles to that of atoms, which kind of packing would the atoms of a given element prefer?

If the atoms are identical and are bound together mainly by dispersion forces which are completely non-directional, they will favor a structure in which as many atoms can be in direct contact as possible. This will, of course, be the hexagonal arrangement.

Directed chemical bonds between atoms have a major effect on the packing. The version of hexagonal packing shown at the right occurs in the form of carbon known asgraphite which forms 2-dimensional sheets. Each carbon atom within a sheet is bonded to three other carbon atons. The result is just the basic hexagonal structure with some atoms missing. [More on graphite here]

The coordination number of 3 reflects the sp²-hybridization of carbon in graphite, resulting in plane-trigonal bonding and thus the sheet structure. Adjacent sheets are bound by weak dispersion forces, allowing the sheets to slip over one another and giving rise to the lubricating and flaking properties of graphite.

Lattices

The underlying order of a crystalline solid can be represented by an array of regularly spaced points that indicate the locations of the crystal's basic structural units. This array is called a crystal lattice.

Crystal lattices can be thought of as being built up from repeating units containing just a few atoms. These repeating units act much as a rubber stamp: press it on the paper, move ("translate") it by an amount equal to the lattice spacing, and stamp the paper again.

The gray circles represent a square array of lattice points.

The orange square is the simplest unit cell that can be used to define the 2-dimensional lattice.

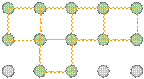Building out the lattice by moving ("translating") the unit cell in a series of steps,

Altough real crystals do not actually grow in this manner, this process is conceptually important because it allows us to classify a lattice type in terms of the simple repeating unit that is used to "build" it. We call this shape theunit cell.

Any number of primitive shapes can be used to define the unit cell of a given crystal lattice. The one that is actually used is largely a matter of convenience, and it may contain a lattice point in its center, as you see in two of the unit cells shown here. In general, the best unit cell is the simplest one that is capable of building out the lattice.

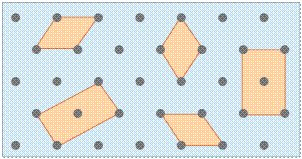
Shown above are unit cells for the close-packed square and hexagonal lattices we discussed near the start of this lesson. Although we could use a hexagon for the second of these lattices, the rhombus is preferred because it is simpler.

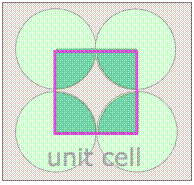Notice that in both of these lattices, the corners of the unit cells are centered on a lattice point. This means that an atom or molecule located on this point in a real crystal lattice is shared with its neighboring cells. As is shown more clearly here for a two-dimensional square-packed lattice, a single unit cell can claim "ownership" of only one-quarter of each molecule, and thus "contains" 4 × ¼ = 1 molecule.

The unit cell of the graphite form of carbon is also a rhombus, in keeping with the hexagonal symmetry of this arrangement.

Notice that to generate this structure from the unit cell, we need to shift the cell in both the x- and y- directions in order to leave empty spaces at the correct spots. We could alternatively use regular hexagons as the unit cells, but the x+y shifts would still be required, so the simpler rhombus is usually preferred.

As you will see in the next section, the empty spaces within these unit cells play an important role when we move from two- to three-dimensional lattices.

Cubic crystals

In order to keep this lesson within reasonable bounds, we are limiting it mostly to crystals belonging to the so-called cubic system. In doing so, we can develop the major concepts that are useful for understanding more complicated structures (as if there are not enough complications in cubics alone!) But in addition, it happens that cubic crystals are very commonly encountered; most metallic elements have cubic structures, and so does ordinary salt, sodium chloride.

We usually think of a cubic shape in terms of the equality of its edge lengths and the 90° angles between its sides, but there is another way of classifying shapes that chemists find very useful. This is to look at what geometric transformations(such as rotations around an axis) we can perform that leave the appearance unchanged. For example, you can rotate a cube 90° around an axis perpendicular to any pair of its six faces without making any apparent change to it. We say that the cube possesses three mutually perpendicular four-fold rotational axes, abbreviated C₄ axes. But if you think about it, a cube can also be rotated around the axes that extend between opposite corners; in this case, it takes three 120° rotations to go through a complete circle, so these axes (also four in number) are three-fold or C₃ axes.

There is even more to cubic symmetry; this NYU page shows all the symmetry operations of the cube; see this video for a live demonstration.

Cubic crystals belong to one of the seven crystal systems whose lattice points can be extended indefinitely to fill three-dimensional space and which can be constructed by successive translations (movements) of a primitive unit cell in three dimensions. As we will see below, the cubic system, as well as some of the others, can have variants in which additional lattice points can be placed at the center of the unit or at the center of each face. This gives a total of 14 possible Bravais lattices on which all crystals (or any repeating array of points in three dimensions) are based.

Date: 2016-01-03; view: 1483