CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Topic: EXPLORING of HARMONIC OSCILLATIONS.
2) Goal:
1. Studying physical pendulum undamped oscillations description method.
2. Studying moment of inertia and equivalent length of physical pendulum determination method.
3) Scheme of laboratory research facility:
|
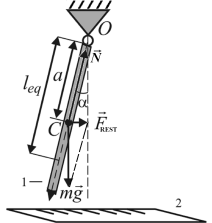
1 physical pendulum;
2 ruler;
O pivot point;
C center of gravity;
leq equivalent length;
α angle of deflection;
a distance between pivot point (axis of rotation)
and center of gravity;
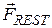 quasi-elastic force;
 supporting force;
 gravity force.
|
4) Table of measuring instruments:
| Ή | Name | Type | Serial Ή | Grid limit | Grid unit | Absolute error |
| 1. | Stopwatch | ΣXΛ-42 | 99,99 s | 0,01 s | 0,01 s | |
| 2. | Ruler | Σ | 1000 mm | 1mm | 1mm |
5) Equations for calculation:
1. Statistical absolute error for direct measurements of period:
,
where a = 0,95 confidence probability; n = 5 number of measurements; t 0,95 ; 5 = 2,77 Students coefficient.
Total absolute error of period
DT = 
,
where DTDEV = 0,01s absolute instrumental error of stopwatch (see Table of measuring instruments).
2. Amplitude of oscillations
A= lsinα ≈ lα 
,
here l length of a pendulum; a = 5O angle of deflection.
Cyclic eigenfrequency of oscillations
,
where <T> average value of period of oscillations.
Initial phase of oscillations:
j0 =p, when initial deflection to the left and x=x(t=0)= A;
j0 =0, when initial deflection to the right and x=x(t=0)= +A.
Equation of oscillations of physical pendulum:
x(t)=Acos(ω0t+φ0);
where x linear displacement of pendulum; t time.
3. Experimentally determined by indirect measurement an average value of moment of inertia:
,
where m mass of a pendulum; g = 9.81 m/s2 acceleration due to gravity; l length of a pendulum.
Absolute error for indirect measurement of moment of inertia:
,
where δJ relative error for indirect measurement of moment of inertia:
,
here 
, 
, 
relative errors for mass, length and period of the pendulum; Δm, Δl, ΔT absolute errors for mass, length and period of the pendulum.
4. Theoretically determined a value of moment of inertia:
.
5. Average value of equivalent length of the pendulum:
.
6) Table of measurements
m = kg; Δm =0,001 kg; l = m; Δl = 0,001 m;
| Ή | ti, s | Ti, s | ΔTi, s | (ΔTi)2, s2 |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| average value <T>= |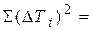 
|
7) Data processing:
8) Final results:
1. T=( <T> ± ΔT)α = (
±
)0.95 s, 
=
%.
2. x(t) = ×cos( t + ) m;
3. JEXP = (< J> ± ΔJ)α = (
±
)0.95 kg·m2, 
=
%;
4. JTHEOR = kg·m2;
5. l eq = m.
9) Conclusion:
(Compare moment of inertia defined experimentally by formula (22) with that of defined by theoretical calculation by formula (23)).
10) Work done by: Work checked by:
WORK 4-3
Date: 2015-12-24; view: 930
| <== previous page | | | next page ==> |
| Harmonic oscillations of physical pendulum | | | DETERMINATION of DAMPED OSCILLATIONS PARAMETERS |