
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Gazprom and the European Union
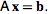
(1)
To perform Gaussian elimination starting with the system of equations
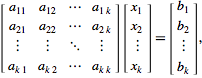
(2)
compose the "augmented matrix equation"
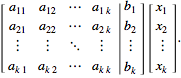
(3)
Here, the column vector in the variables 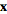 is carried along for labeling the matrix rows. Now, perform elementary row operations to put the augmented matrix into the upper triangular form
is carried along for labeling the matrix rows. Now, perform elementary row operations to put the augmented matrix into the upper triangular form
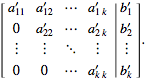
(4)
Solve the equation of the 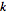 th row for
th row for  , then substitute back into the equation of the
, then substitute back into the equation of the  st row to obtain a solution for
st row to obtain a solution for  , etc., according to the formula
, etc., according to the formula
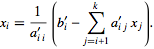
(5)
In Mathematica, RowReduce
performs a version of Gaussian elimination, with the equation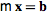 being solved by GaussianElimination[m_?MatrixQ, v_?VectorQ] := Last /@ RowReduce[Flatten /@ Transpose[{m, v}]]
being solved by GaussianElimination[m_?MatrixQ, v_?VectorQ] := Last /@ RowReduce[Flatten /@ Transpose[{m, v}]] LU decomposition of a matrix is frequently used as part of a Gaussian elimination process for solving a matrix equation.
A matrix that has undergone Gaussian elimination is said to be in echelon form.
For example, consider the matrix equation
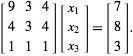
(6)
In augmented form, this becomes
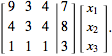
(7)
Switching the first and third rows (without switching the elements in the right-hand column vector) gives
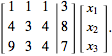
(8)
Subtracting 9 times the first row from the third row gives
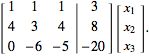
(9)
Subtracting 4 times the first row from the second row gives
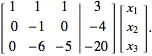
(10)
Finally, adding 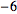 times the second row to the third row gives
times the second row to the third row gives
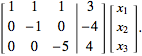
(11)
Restoring the transformed matrix equation gives

(12)
which can be solved immediately to give  , back-substituting to obtain
, back-substituting to obtain 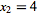 (which actually follows trivially in this example), and then again back-substituting to find
(which actually follows trivially in this example), and then again back-substituting to find 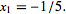
Gazprom and the European Union
Date: 2015-01-02; view: 1599
| <== previous page | | | next page ==> |
| Gaussian elimination is a method for solving matrix equations of the form | | | The European Union squeezes Gazprom. Russia retaliates |