B) The mild temperature was lowered by a heavy rain in the morning, and the temperature dropped lower by evening. 6 page

(A) $1.50

(B) $2.00

C) $3.00

(D) $4.00

(E) $6.00

3. In the figure below, line passes through the origin and has a slope of 2. What is the value of k?

(A) 2

(B) 4

(C) 6

(D) 12

(E) 24

4. If x is 5 less than y, then what is the value of 5(x − y)?

(A) - 25

(B) - 5

(C) 0

(D) 5

E) 25

5. On a certain map that is drawn to scale, a distance of 50 miles is represented by 1 inch. How many inches on the map would represent a distance of 240 miles?

(A) 2.4

B) 4.8

(C) 6.4

(D) 8.0

(E) 12.0

6. Three students have a total of 30 CDs among them. If one student has 40% of the CDs, and another has 33 ¹/₃% of the CDs, how many CDs does the third student have?

(A) 6

(B) 8

(C) 9

(D) 10

(E) 12

7. The average (arithmetic mean) of Marianne’s scores on three tests is 85. If she scored 90 on both of the first two tests, what was her score on the third test?

(A) 70

B) 75

(C) 80

(D) 85

(E) 90

8. The numbers - 1, 0 and 1 repeat in a sequence, as shown below. If this pattern continues, what will be the sum of the first 100 terms of this sequence?

- 1, 0, 1, - 1, 0, 1…

(A) - 1

(B) 1

(C) 33

(D) 34

(E) 100

9. Fifty plastic balls numbered 1 to 50, inclusive, are placed in a bowl and one ball is to be selected at random. What is the probability that the ball selected will have a number that is a multiple of 3?

(A)

(B)

(C)

(D)

(E)

10. If a + b = 5, a − c = 15, and a = 10, then c − b =

(A) - 10

(B) - 5

C) 0

(D) 5

(E) 10

11. In the correctly worked addition problem below, A and B represent digits. What is digit A?

(A) 5

(B) 6

(C) 7

D) 8

(E) 9

12. In the figure below, point D (not shown) is drawn so that point C is the midpoint of . If

CD = 4x, then what is the length of AB in terms of x?

(A) 3x

(B)

(C) 4x

(D)

(E)

13. The line that passes through (− 2, 4) and (1, 6) also passes through which of the following points?

(A) (4, 8)

(B) (4, 10)

(C) (5, 7)

(D) (5, 8)

(E) (5, 9)

14. For which of the following sets of numbers is the first number equal to the sum of the second number and the square of the third number?

(A) 6, 4, 2

(B) 9, 6, 9

(C) 10, 9, 4

(D) 16, 7, 3

(E) 19, 16, 15

15. 3^x + 3^x + 3^x + 3^x + 3^x + 3^x + 3^x + 3^x + 3^x =

(A) 3^x+8

(B) 3^9x

(C) 3^x+2

(D) 27^x

(E) 9(3^9x)

16. Which of the following graphs represents the set of all solutions of the statement 2 − | x + 1| < 0?

(A)

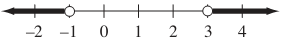
(B)

(C)

(D)

(E)

17. A publishing company wants to increase the price of one of its books by 10%. Research shows that this increase in price would de-crease sales of the book by only 5%. By what percent would this change increase the money received through sales of this book?

(A) 4.0%

(B) 4.5%

(C) 5.0%

(D) 5.5%

(E) 6.0%

18. A total of 32 teams play in a single-elimination tournament. In the first round, every team plays one game against another team, and the losing teams are eliminated from the tournament. No game ends in a tie. Every winning team pro-cedes to the next round, in which they play another winning team. This single-elimination procedure continues until only one team remains. If each game takes precisely 2 hours to play, what is the total length of games played in the tournament, in hours?

(A) 30

(B) 32

(C) 48

(D) 62

(E) 64

19. In the figure below, points A, B, and C are vertices of the cube shown. What is the area of triangle ABC?

(A) 50

(B) 50

(C) 50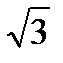

(D)

(E)

20. A jar contains only red and black marbles. Originally, the ratio of black marbles to red marbles was 4:5. After 18 black marbles were added, the ratio of black marbles to red marbles became 5:4. How many marbles were in the jar originally?

(A) 45

(B) 54

(C) 63

(D) 72

(E) 81

21. If and 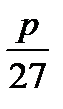are both integers, then what is the least possible positive value of p?

(A) 3

(B) 6

(C) 9

(D) 18

E) 27

22. If 4(x + 3) = 15, then what is the value of 4x + 3?

(A)

(B)

C) 6

(D) 10

(E) 15

23. In a road race, a $4,000 prize is split among the first three finishers in the ratio of 5:2:1.

What is the greatest amount, in dollars, that any of the three prize winners receives?

(A) 500

(B) 1000

(C) 1500

(D) 2000

(E) 2500

24. Point O is the center of the circle below, arc MNP has a length of 6π and MOP has a measure of 120°. What is the length of PO?

(A) 6

(B) 9

(C) 12

(D) 15

(E) 18

25. In the figure below, AB = BC. What is the value of y?

(A) 40

B) 50

(C) 65

(D) 70

(E) 75

26. The average (arithmetic mean) of f, g and h is one greater than their median, and f < g < h.

If f = 6 and h = 20, then what is the value of g?

(A) 9

(B) 10.5

(C) 11.5

(D) 12

(E) 23

27. A jar contains marbles that are either red, white or blue. If the ratio of white marbles to red marbles is 3 to 5 and the ratio of red marbles to blue marbles is 6 to 5, then what is the least possible number of marbles in the jar?

(A) 18

(B) 25

(C) 63

(D) 73

(E) 80

28. The volume of a certain quantity of gas varies inversely as the pressure (in atmospheres) and directly as the temperature (in degrees Kelvin). If this quantity of gas occupies 10 liters at a pressure of 2 atmospheres and a temperature of 300 degrees Kelvin, what volume, in liters, will it occupy at 1 atmosphere and 450 degrees Kelvin?

(A) 15

(B) 30

(C) 90

(D) 300

(E) 450

29. Find the second order derivatives of the function

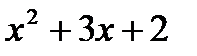
(A) 1

(B) 2

C) 3

(D) 4

(E) 5

30. Find the integral of the function in the below.

(A)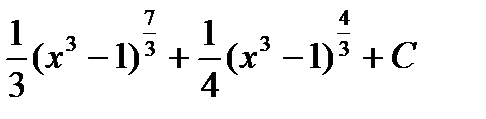

(B)

(C)

(D)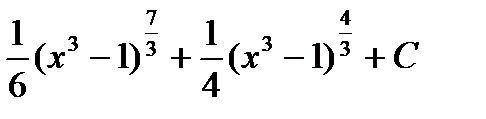

(E)

TEST 13

1. If (x − y) = − 2, then 3(x − y)(x − y)(x − y) =

(A) - 24

(B) - 12

(C) 0

(D) 12

(E) 24

2. If w ≠ 0, then 40 percent of 20w is equal to

(A) 2w

(B) 4w

(C) 8w

(D) 20w

(E) 80w

3. The table below shows a relationship between two variables, x and y. Which of the following equations could describe this relationship?

(A) y = x + 7

(B) y = 4x - 2

(C) y = 3x + 1

(D) y = 5x - 5

(E) y = 2x + 4

4. The points W, X, Y, and Z lie on a line in that order. If XY= 50, WY is 30 more than XY, and

WX = YZ, what is XZ?

(A) 30

(B) 50

(C) 70

(D) 80

(E) 100

5. In the cube in the figure below, all of the following line segments are the same length except

(A) AG

(B) BE

(C) BD

(D) EG

(E) AE

6. If 3^{y + 4}= 81, what is the value of y?

(A) - 2

(B) - 1

(C) 0

(D) 1

(E) 2

7. In the figure below, what is the value of x + y?

(A) 120

(B) 110

(C) 100

(D) 90

(E) 80

8. If a and b are non-zero integers and a > b, which of the following must be true?

I. ab ≠ 0

II. a − b > 0

III. a ÷ b > 1

(A) I only

(B) II only

(C) I and II only

(D) I and III only

(E) I, II, and III only

9. The distance from Appletown to Brickton is 6 miles and the distance from Brickton to

Caper City is 9 miles. Which of the following could be the distance, in miles, from Appletown to Caper City?

(A) 14

(B) 16

(C) 17

(D) 18

(E) 19

10. The figure below shows five triangles arranged around a regular pentagon. All of the solid line segments are equal in length. If the perimeter of the figure indicated by the solid segments is

100 and the perimeter of the pentagon indicated by the dotted lines is 60, what is the area of one of the triangles?

(A) 24

(B) 32

(C) 36

(D) 48

(E) 64

11. The sum of two numbers is 71. If one number is 2 greater than one-half of the other number, what is the value of the greater number?

(A) 23

(B) 25

(C) 42

(D) 43

(E) 46

12. Points A, B, C, and D lie on line l and points D, E, F, and G lie on line m. If lines l and m are distinct, how many lines can be drawn such that each line passes through exactly 2 of these 7 points?

(A) 4

(B) 5

(C) 6

(D) 9

(E) 12

13. What fraction of the even integers between 2 and 16, inclusive, satisfy the statement 3w − 2 > 28?

(A)

(B)

(C)

(D)

(E)

14. If a is 20 percent less than b, and b is 20 percent greater than 400, then what is the value of b − a?

(A) 80

(B) 96

(C) 100

(D) 104

(E) 108

15. If m = n(n − 3), what is the value of − 3m in terms of n?

(A) 3n + 3n²

(B) 9n + 3n²

(C) 3n + 9n²

(D) 3n - 3n²

(E) 9n - 3n²

16. In the figure below, ABCD is a rectangle and points E and F are midpoints of their respective sides. If BC = 2AB = 8, what is the area of ΔEFD?

(A) 8

(B) 12

(C) 16

(D) 20

(E) 24

17. What is the average (arithmetic mean) of 8 consecutive odd integers if the least of these integers is x?

(A) x + 5

(B) x + 6

(C) x + 7

(D) x + 8

(E) x + 9

18. In the figure below 20 < b < 30 and a > c > b. If a, b and c are integers, what is the largest possible value of a?

(A) 119

(B) 121

(C) 140

(D) 137

(E) 139

19. If and 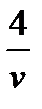+ w = 6 and v 0, which of the following expresses v in terms of w?

(A)

(B)

(C)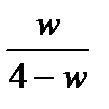

(D)

(E)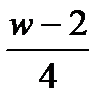

20. The distance from the center of a clock to the tip of the minute hand is 4 inches. What is the length of the arc, in feet, that this tip traces between 2:45 pm and 7:15 pm? (1 foot = 12 inches)

(A)

(B)

(C)

(D)

(E)

21. If and a = 36, then b =

(A) 12

(B) 24

(C) 28

(D) 32

(E) 54

22. If 2c + d = 9.25, then 6c + 3d + 3 =

(A) 22.75

(B) 24.75

(C) 27.75

(D) 30.75

(E) 32.75

23. If the shaded triangle in the figure below has an area of 12, what is the value of m?

(A) 2

(B) 4

(C) 6

(D) 8

(E) 10

24. A pizzeria offers one or more of the following toppings on its pizzas: pepperoni, mushrooms, meatballs. How many different combinations of one or more toppings are possible? (Assume that the order of the toppings does not matter.)

(A) 5

(B) 6

(C) 7

(D) 8

(E) 9

25. If the perimeter of a rectangle is 5 times the width of the rectangle, then the length of the rectangle is how many times longer than the width?

(A)

(B)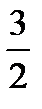

(C) 2

(D)

(E) 3

26. If 16^{w + 2} = 2¹¹, what is the value of w?

(A) 0.75

(B) 1.33

(C) 2.00

(D) 3.50

(E) 4.75

27. In the figure below, ABCD is a parallelogram and AE bisects ∠DAB. What is the value of x?

(A) 24

(B) 28

(C) 32

(D) 36

(E) 40

28. The width of a rectangle is 75% the length of the rectangle. The perimeter of the rectangle is 84 centimeters. A circle is drawn that contains all four vertices of this rectangle. If the area of this circle is kπ square centimeters, what is the value of k?

(A) 160

(B) 175

(C) 185

(D) 210

(E) 225

29. Find the second order derivatives of the function

(A)

(B)

(C)

(D)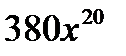

(E)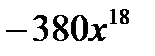

30. Find the integral of the function in the below.

(A)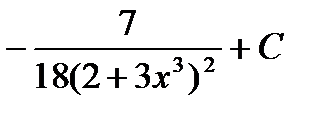

(B)

(C)

(D)

(E)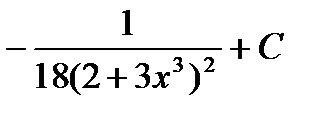

TEST 14

1. If 2x + 7 = 4x + 5, what is the value of x?

(A) 1

(B) 2

(C) 4

(D) 5

(E) 8

2. If n is any positive integer, which of the following must be even?

(A) n + 2

(B) 2n

(C) 3n

(D) n²

(E) n³

3. The length of a nail rounded to the nearest inch is 5 inches. Which of the following could be the actual length of the nail, in inches?

(A) 4.46

(B) 4.48

(C) 5.32

(D) 5.51

(E) 5.89

4. The walls of Jane’s living room have an area of 340 square feet. If she can paint 60 square feet per hour, how many minutes after she starts painting will there be only 100 square feet left to paint?

(A) 120

(B) 150

(C) 180

(D) 240

(E) 270

5. In the right triangle below, what is the value of 3x?

(A) 18.0

(B) 22.5

(C) 27.0

(D) 30.0

(E) 67.5

6. What is 50% of 60% of 180?

(A) 48

(B) 54

(C) 60

(D) 90

(E) 92

7. If 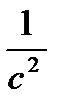= b² + 4b + 4 then c =

(A)

(B)

(C)

(D)

(E)

8. If the average of 3y, 4y, and (y − 5) is 9, what is the value of y?

(A) 1.50

(B) 1.75

(C) 2.00

(D) 3.25

(E) 4.00

9. In the figure below, right triangle ABC has side lengths as shown. What is the value of x?

(A) 2

(B) 3

(C) 4

(D) 5

(E) 6

10. Which of the following represents the set of all values of x for which is defined the function f(x) = ?

(A) x - 4

(B) x > - 4

(C) x - 4 and x 6

(D) x > - 4 and x 6

(E) x 6

11. When the positive integer w is divided by 6, the remainder is 2. What is the remainder when 5w is divided by 6?

(A) 1

(B) 2

(C) 3

(D) 4

(E) 5

12. Given the information in the table below, what is the value of x + y + z?

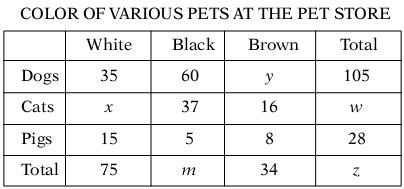
(A) 35

(B) 113

(C) 246

(D) 299

(E) 314

13. If a circle with center (3, 4) is tangent to the x-axis, what is the circumference of the circle?

(A) 4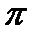

(B) 6

(C) 8

(D) 12

(E) 16

14. If the length of line segment is 7 and the length of line segment is 9, which of the following could not be the length of line segment ?

(A) 6

(B) 8

(C) 12

(D) 16

(E) 18

15. In the figure below, line m passes through the origin. Which of the following points lies on line m?

I. (− 2, 1)

II. (− 2, − 2)

III. (1, 1)

(A) I only

(B) I and II only

(C) I and III only

(D) II and III only

(E) I, II, and III

16. In the figure below, WX = XZ= ZY. What is the value of b?

(A) 56

(B) 76

(C) 78

(D) 84

(E) 128

17. In one day, Mitchell spends 30% of the day sleeping, 35% of the day at work, 5% of the day at the gym, five additional hours at home, and the rest of the day in the car. How many minutes does he spend in the car each day? (1 hour = 60 minutes)

(A) 2.2

(B) 60

(C) 120

(D) 132

(E) 432

18. What is the slope of the line containing the point (2, 5) and the midpoint of the line segment with endpoints (8, 8) and (6, −2)?

Date: 2015-12-24; view: 1424