
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Module 2. Analitic geometry. Introduction to Calculus
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 1
1. Calculate the limits: à)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
2. Calculate the limits: à)  ; b) .
; b) .  .
.
3 Investigate the function for continuity:  .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 2
1. Calculate the limits: à)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function  for continuity.
for continuity.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 3
1Calculate the limits: à)  ; b)
; b)  ;
;
c) 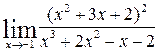 ; d)
; d)  .
.
4. Calculate the limits: à) 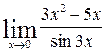 ; b) .
; b) .  .
.
5. Investigate the function for continuity:  .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 4
1. Calculate the limits: à)  ; b)
; b)  ;
;
c) 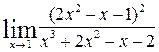 ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity: 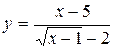
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 5
1.
Calculate the limits: à)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity: 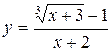
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 6
1.. Calculate the limits: à) 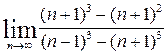 ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity: 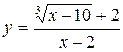 .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 7
1.. Calculate the limits: à)  ; b)
; b) 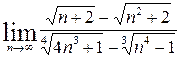 ;
;
c)  ; d)
; d) 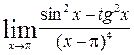 .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity:  .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 8
Calculate the limits: à)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity: 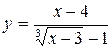 .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 9
1Calculate the limits: à) 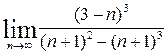 ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
4. Calculate the limits: à)  ; b)
; b)  .
.
5. Investigate the function for continuity:  .
.
Module 2. Analitic geometry. Introduction to Calculus
Individual Home Task
Variant 10
1. Calculate the limits: à)  ; b)
; b)  ;
;
c)  ; d)
; d) 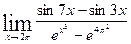 .
.
5. Calculate the limits: à)  ; b)
; b)  .
.
6. Investigate the function for continuity: 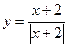
Module 2. Analitic geometry. Introduction to Calculus
Date: 2015-12-24; view: 1207
| <== previous page | | | next page ==> |
| Other Functions of Money. Äðóãèå ôóíêöèè äåíåã | | | Individual Home Task |