Linear approximations of physical systems

Examination cards on Control systems (307 group)

Examination card #1

Differential equations of physical systems

3: Performance parameters of control systems in the transient process

2: Feedback control loops and their influence on dynamic and static characteristics of control systems

Examination card #2

Linear approximations of physical systems

3: Effects of a third pole and a zero on the second-order system response

4: Example 46.2 (Lecture 4.4): full-state feedback control design for a 3^rd order control system which is described by the following differential equation

Examination card #3

The differential motion equation of control systems

4: Similarity transformation

PID controller design

Examination card #4

1: Superposition principle

4: Controllable Canonical Form

2: Stationary and non-stationary random processes

Examination card #5

2: The connection diagrams of dynamic links

3: Sensitivity of control systems to parameter variations

1: Construct logarithmic gain-frequency characteristic:

Examination card #6

2: Directed (oriented) graphs of control systems

3: Steady-state errors of control systems

4: Example 46.6 (Lecture 4.4): design a system which controls a satellite using the Ackerman’s formula

Examination card #7

2: Mason's gain rule

4: Observable Canonical Form

3: Define the system sensitivity to the change in its parameters.

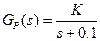
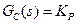
Examination card #8

2:Cramer’s rule

4: Controllability

1: Construct asymptotic logarithmic gain frequency characteristics:

Examination card #9

Linear approximations of physical systems

3: Gain and phase margins of control systems

2: Static characteristics of control systems

Examination card #10

1: The Laplace transform

3: Assessing stability indicators using Nichols diagrams

4: State observers

Examination card #11

1: The transfer function of linear systems

4: Observability

3: Research the behaviour of the following control system with output delay:

Examination card #12

1: Construct logarithmic gain-frequency characteristics:

4: Kalman decomposition

2: Power spectral density (spectral concentration)

Examination card #13

2: State Variable Models of linear control systems (the state differential equations and output equation)

3: Control System’s Bandwidth

1: Typical dynamic links of control systems and their characteristics (overdamped links: )

Examination card #14

2: Signal-flow graph and block diagram models

3: The stability of control systems with time delays

4: Reduced order state observers

Examination card #15

2: Random signal passage via linear control systems

4: Full-state feedback control design

3: Construct Nyquist, Bode and Nichols diagrams and define stability indicators for the following transfer function:

Examination card #16

2: The transfer function from the state equation

4: Reference inputs

1: Typical dynamic links of control systems and their characteristics (undamped links: )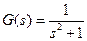

Examination card #17

1: Test input signals (step function and -function)

3: Step 4: Locating the segments of the real axis that are root loci.

2: White noise fluctuations

Examination card #18

1: Test input signals (harmonic input signal, ramp input signal, quadratic and cubic input time power functions)

3: Step 7: Locating asymptotes of root loci

4: The analysis of the motion of a relay control system

Examination card #19

1: Frequency characteristics of control systems

4: Internal model design

3: Research the behaviour of the following control system with input delay:

Examination card #20

1: The notion of a link

4: Phase Plane Analysis of control systems (case 3)

2: Methods to analyse the errors of linear control systems at random input signals

Examination card #21

2: The concept of stability

3: Step 9: Defining the breakaway points from real axis

1: Typical dynamic links of control systems and their characteristics (integrating links: )

Examination card #22

2: Moments of random processes

3: Step 10: Defining the angle of departure of the locus from a pole and the angle of arrival of the locus at a zero

4: Example 50.1 (Lecture 4.8): ideal relay (“sign” block)

Examination card #23

2: Lyapunov Stability of Linear Systems

4: Singular lines for nonlinear control systems

3: Construct the root locus for the following transfer function

Examination card #24

2: Routh-Hurwitz stability criterion

4: Limit Cycle

1: Typical dynamic links of control systems and their characteristics (differentiating links: )

Examination card #25

1: Logarithmic frequency characteristics (the Bode diagram)

3: Parameter design by the root locus method

2: 14 Define state-space model for the following transfer function

Examination card #26

1: Logarithmic gain-phase characteristic (the Nichols diagram)

3: Phase-lead network

4: Common Nonlinearities

Examination card #27

1: The connection between a transient characteristic 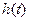, weighting function 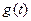and transfer function

4: Lyapunov stability theory (the direct method of Lyapunov)

3: Construct Nyquist, Bode and Nichols diagrams and define stability indicators for the following transfer function:

Examination card #28

1: Typical dynamic links of control systems and their characteristics (amplification links: )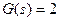

4: Sliding Mode Control

2: Anti-parallel coupling of links

Write down Matlab script in order to define the equivalent transfer function.

Examination card #29

2: Nyquist stability criterion

3: Phase-lag network

1: Construct asymptotic logarithmic gain frequency characteristic:

Examination card #30

2: Cauchy's theorem

3: Compensator design by changing a system gain

4: Describing function

Examination card #31

2: Relative stability and the Nyquist criterion

4: Back-stepping Design

3: Construct asymptotic logarithmic gain-frequency characteristic for the following transfer function:

Examination card #32

2: Bode diagram of control systems

4: High-gain observers

1: Typical dynamic links of control systems and their characteristics (under-damped links: )

Date: 2015-12-24; view: 2772