
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Digital Logarithmic (DL) Representation
Contents
| 1. Objectives of the Term Work_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ | |
| 2. Basic Principles _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ | |
| 2.1. Digital Logarithmic (DL) Representation _ _ _ _ _ _ _ _ _ _ _ _ _ | |
| 2.2. Basic Rules of DLArithmetic _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ | |
| 2.3. Basic Algorithms of Data Processing _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ | |
| 3. Models of Data Structures in the Main Memory _ _ _ _ _ _ _ _ | |
| 4. Processing the DL-Type of Data in Computer _ _ _ _ _ _ _ _ | |
| 5. Solution of the Task of Term Assignment_ _ _ _ _ _ _ _ _ _ _ | |
| 6. Attachment. The Source Code of the Developed Class _ | |
| Bibliography_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ |
Objectives of the Term Work
The term work in the discipline “Computer Modeling and Simulation” is aimed at students mastering the principles of building inductive models with self-organization, namely, applications of the structural-programming principle for the development of models of calculation (processing).
The term “structural” is used to denote principles and methods of building a model. An arithmetic-algorithmic basis for the development of models is proposed. This basis is a digital-logarithmic (DL) representation of data structures and it satisfies a sufficient level of the simulation accuracy. A construct-operational development of such representation is application of special computer arithmetic.
Application of such arithmetic-operational tool ensures increasing the range of calculation up to a value that allows excluding rounding and normalization, provides solution of tasks sensitive to errors.
A model of calculation must be developed according to the principles of inductive models. Realization of the inductive approach lies in the application of automatic changing of the calculation range, which provides the accuracy of the solution.
Self-organization and self-instruction are realized as a process of choosing the range formation via the parameters of the binary word length and data word length. The development of an inductive model is realized by the appropriate routine using a high-level programming language such as Ñ, Ñ++, FORTRAN, PASCAL etc.
The object of design in the term work is an algorithm of calculation–processing on the basis of DL arithmetic and on the principles of self-organization.
Basic Principles
Digital Logarithmic (DL) Representation
Fundamentals of data representation in a computer are numerical systems. A numerical system is a method of representation and notation (writing) of numbers, which is defined by a set of rules and formulae [1-2]. When constructing numerical systems, the following things are considered first of all:
- the range of number representation;
- uniqueness of representation: a code combination corresponds to one and only one number in a given range of numbers;
- constructivity in performing the operations of addition and multiplication;
- operations of conversion from one numerical system into another and vice-versa;
- possibility to increase the speed of performing operations in the future;
- operational devices performing algorithms of processing are easy to control;
- processability of realized operations built on the arithmetic-logical basis of a chosen numerical system.
One of the basic tendencies in the development of computer engineering is application of non-traditional data coding-depicting. So, in spite of principal differences between positional and non-positional coding, a possibility of uniting these two systems into one which would have positive features of its components has been proven [1-2].
Investigating the possibilities of application of non-traditional codes for realization of multiplicative operations as well as general requirements to constructivity of data coding (possibilities of operations performing), original data coding has been proposed, which has got the name Digital Logarithmic (DL) [1-2].
Definition. Digital Logarithmic (DL) representation (coding) of data is a depicting of a binary operand in the form of a set of binary codes of non-zero digits {Nxi} of the same operand, each of which is determined as the result of calculating the binary logarithm of this digit’s weight:
xi  {Nxi = log2xi * pi | xi
{Nxi = log2xi * pi | xi 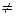 0},
0},
where õi is a non-zero digit, ð is the radix of the numerical system.
The basic concepts of DL data representation are given in [1-2]. Any positive number À may be represented in terms of finite or infinite fractions [1-4]:

or  , where
, where  are digits of the number À (a set of digits depends on the radix of a numerical system), p is the radix of a numerical system, am is the most significant digit of the number À.
are digits of the number À (a set of digits depends on the radix of a numerical system), p is the radix of a numerical system, am is the most significant digit of the number À.
In DL representation, each binary non-zero digit  is represented as a code
is represented as a code  , which is determined as a binary logarithm of the quantity represented by this digit:
, which is determined as a binary logarithm of the quantity represented by this digit:
 (
(  ).
).
In other words,  is the number (code) of a non-zero digit. The number À (numerical operand) is depicted as a set of binary codes
is the number (code) of a non-zero digit. The number À (numerical operand) is depicted as a set of binary codes  . For example, the fixed-point binary number
. For example, the fixed-point binary number 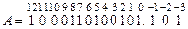 in DL-representation takes the form: À=12.8.7.5.2.0.-1.-3.
in DL-representation takes the form: À=12.8.7.5.2.0.-1.-3.
From the practical point of view, the most convenient structure for using DL-representation of the number A is that which contains the sign of the number A, the number of its significant digits, and the set of DL codes. The general view of such a structure is:
A  signAQAN1N2N3N4…NQ,
signAQAN1N2N3N4…NQ,
where  is the field of the sign of A (0 for a positive number and 1 for a negative number),
is the field of the sign of A (0 for a positive number and 1 for a negative number),  is the field of the number of significant digits, and
is the field of the number of significant digits, and  is the field of DL codes. For the mentioned above example, the number À is depicted as ÀDL= 0.8.12.8.7.5.2.0.-1.-3.
is the field of DL codes. For the mentioned above example, the number À is depicted as ÀDL= 0.8.12.8.7.5.2.0.-1.-3.
Conversion from the binary representation of À to the form, where each non-zero digit is represented by its number, is determined unambiguously and realized without additional functional conversions –operations of substitution are performed for each non-zero digit.
The binary operands À = +111111000111 and  = +10100100001 in DL codes are: ÀDL = 0.9.11.10.9.8.7.6.2.1.0. and BDL = 0.4.10.8.5.0.
For the reverse conversion into binary representation (binary code), a decoding operation must be done.
The use of DL representation makes it possible to build a common structure for floating-point and fixed-point formats. For each number of a non-zero digit in the floating-point format, the representation capacity must be increased by 1 bit; the value of the order is added to each number if this order is the power index of 2.
Consequently, the structure of generalized representation for floating-point and fixed-point formats has the form (p is the exponent of A):
| Sign A | Q | ± N1 ± p | ± N2 ± p | … | … | ± NQ ± p |
The same structure is applicable for the natural point. Thus, when using DL coding, data – numerical operands (integers, fractions, and mixed fractions) – have the same structure of representation.
The set of numbers depicted in the DL code has the following features:
- DL coding (representation) is a limited subset of rational numbers;
- the set of DL codes is symmetric about the number zero;
- DL elements are uniformly distributed along the line of real numbers, which significantly increases the precision of data representation.
Representation of the number zero in DL coding should be pointed out. A factor Q characterizing the number of significant digits is used in each operand of DL-code structures. If an operand is equal to zero, the factor Q is equal to zero too (Q = 0), i.e. the operand has no significant digits. Such representation of zero in the computer environment is the most precise since it corresponds to the physical treatment of the zero value but not to the mathematical model accepted in different computers.
Thus, each DL-representation of a number in the computer environment is a one-dimensional array. Such an array is programmed with elements of “INTEGER” type as the position numbers of non-zero digits are integer numbers.
DL coding (representation) is a hierarchical system with an alphabet (carrier) which coincides with the alphabet of the binary system, the onto function being a logarithmic function the domain of which are the non-zero digits of operands
 S : À2
S : À2 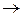 ÀDL,
ÀDL,  S = log2 aipi .
S = log2 aipi .
In DL-representation (coding), the numeric range extends significantly. The range of number representation increases by several orders according to the sizes of the bit net of the computer or computer environment employed [1-2]. It is due to the fact that it is not of the number A itself that is represented in the bit-net, but sets of codes  , that are numerically (equal to) the binary exponents of significant digits in the binary form of the number À. The above-mentioned elements
, that are numerically (equal to) the binary exponents of significant digits in the binary form of the number À. The above-mentioned elements  constitute the DL form of the number, and the computer’s bit net is used for their representation.
constitute the DL form of the number, and the computer’s bit net is used for their representation.
Thus, under the traditional approach, the maximal integer sign number, in the case of an n-bit net, may be written as: Amax = 2n-1 -1, and in DL coding it is Amax DL = 2mm -1, where mm=2n-1 -1-(one bit is allotted for the sign of the binary number).
Table 2.1 shows how the range of binary numbers, the length of the DL code, and the range of DL numbers depend on the length of the binary code. The extension of the data representation range reduces the influence of rounding on the accuracy of calculation.
Table 2.1
Comparative characteristic of binary and DL representation by the data range
| Binary code length | Range of binary numbers | DL code length | Range of DL numbers |

| 
| ||

| 
| ||

| 
| ||

| 2+2147483647 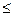 À À 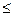 2-2147483647
2-2147483647
|
For the DL system, the coverage of the numeric axis is uniform in the whole chosen range (Fig. 2.1).
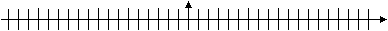
0(zero)
Fig. 2.1. Coverage of the numeric axis in DL coding
Such coverage is achieved by increasing the number of elements representing significant digits in the code array. It is significant that such an increase of mantissa is not mechanistic, and the full coverage of the numeric axis, as modeling of numeric structures shows, is provided by an increase of the total bit capacity.
Here, the chief feature of DL coding is a unified structure for all number types. No other numeric system allows an exact representation of such a number, e.g.:
À = +. 2. +1637833. -187183738.
The mantissa of a number À in the DL representation is a field of DL codes with the appropriate structure and format of this number:
Integer part Fractional part
| SignA A | QA | -1 | -3 | -7 | -19 |
The integer part of a DL number is a set of the mantissa digits Mi, which are more than or equal to zero; the fractional part is a set of the mantissa digits Mj, which are less than zero, i.e. have the sign of minus. The digit sets of the fractional and integer parts of the number may be ordered in a definite order or positioned in the mantissa in an arbitrary order. The both sets are not divided in the mantissa and represent the unique field of the number DL codes.
In DL data representation, there is no need in mantissa normalization. DL representation excludes the procedure of normalization used in the binary representation of operands in computers.
The mantissa of a DL number, for a fixed number of bits may represent a binary number with the same number of bits (if all the digits of the binary number are equal to 1), or with a much larger number of bits when at the expense of zero digits, provided a given number of significant digits, it is possible to save, along with the most significant digits of the number, its least significant digits, which are usually eliminated in the binary representation.
The mantissa of a DL number may also have a non-fixed number of bits. After arithmetic operations performed in DL representation, this number may either increase or decrease as compared to the initial number of bits in the operands (at the beginning of problem solution). The conditions of using DL structures in computer processing also allows setting a necessary number of bits in the mantissa required to improve the calculation accuracy. This can be done either at the beginning or in the course of the computational process.
Date: 2015-12-24; view: 1057
| <== previous page | | | next page ==> |
| Cloning extinct and endangered species | | | Models of Data Structures in the Main Memory |