
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Travail pratique ¹ 14
6.2.14.1 Résolution d’un système des équations linéaires, opérations avec des matrices
Objectif de travail: réception de l’expérience de la résolution de systèmes des équations linéaires, opérations avec des matrices au milieu MS Excel.
On va se rappeler les notions générales exposées en discipline « Mathématique » qui touchent le problème posé.
Résolution d’un système des équations algébriques linéaires (SÉAL).
On a donnés un système des équations algébriques linéaires sous forme:

Ce système peut être présenté sous forme d’un produit matriciel:
A*x=b
où
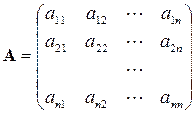 – matrice des coefficients de système;
– matrice des coefficients de système;
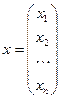 – vecteur des inconnues,
– vecteur des inconnues,  – vecteur des parties droites.
– vecteur des parties droites.
Résolution d’un système des équations algébriques linéaires posé dans ce travail pratique doit être fait par la méthode de Cramer Gabriel et matrice inverse.
Les formules principales utilisées dans ces méthodes.
Méthode de la matrice inverse
Pour chaque nombre a le nombre inverse est 
 . Ce dernier est désigné encore comme a -1. De la manière analogue A-1estla désignation de la matrice inverse pour la matrice A.Le produitA -1 × A = E.
. Ce dernier est désigné encore comme a -1. De la manière analogue A-1estla désignation de la matrice inverse pour la matrice A.Le produitA -1 × A = E.
Eestla matrice unité.Touts les elements de cette matrice sont égaux à unité. La multiplication chaque partie de l’équation A×x= b par A -1 de guache donne:
A-1×A×x= A-1×b, E×x=A-1×b,(E – la matrice unité)
Autrement dit le vecteur des inconnues x est calculé par la formule:
x=A-1×b.
Méthode de Cramer
La méthode de Cramer prevoit le calcul des inconnues x1, x2,…, xn selon la formule:

où D – est le déterminant de la matrice A,
Di – est le déterminant de la matrice formée en remplaçant i–éme colonne de la matrice A par le vecteur colonne b.
Faites attention :
avant de faire les opérations avec des matrices il faut toujour sélecter préalablement la zone pour le résultat.
Pour bien assimiler le sens des méthodes mentionnées on propose examiner les problèmes suivants.
Exemple 1.
Il faut résoudre le système suivant par la méthode de la matrice inverse.
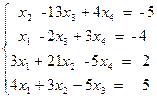
Dans ce cas la matrice de coefficients À et vecteur colonne b ont la forme suivante:
 ,
,  .
.
1– er étape.
L’entrée de la matrice A et vecteur b dans la feuille active MS Excel (fig. 6.34).

Fig. 6.34
La matrice À occupe la plage des cellules B1:Å4, vecteur b – la plage G1:G4.
2– ème étape.
Le calcul de la matrice inverse A -1.
Cette action est réalisé de la manière suivante:
– sélectionner la plage de cellules B6:E9pour la matrice inverse A -1 ;
–cliquer sur l’icône fx en passant à premier pas d’assistant formule;
– cliquer sur la catégorie Ìàòåìàòè÷åñêèåde la boîtequi s’affiche et dans la case déroulante de cette boîte cliquer sur le nom ÌÎÁÐ(fig.6.35) et puis sur le boutonOK de cette boîte en passant à deuxiéme pas;
– cliquer sur la case Ìàññèâ(fig. 6.36). Après avoir apparu d’un pointeur te texte dans cette case il faut sélecter la plage de cellules B1:Å4réservée pour la matrice À.Cet diapason estapparu dans la case;
–cliquer sur le bouton OKde cetteboîte.

Fig. 6.35
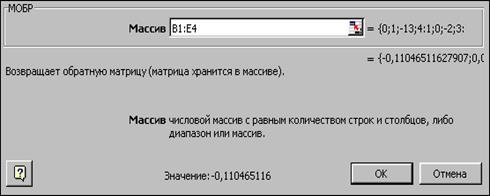
Fig. 6.36
Après ces actions un nombre s’affiche dans la première cellule de la plage réservée pour la matrice inverse.
Pourobtenir la matrice inverse il fautappuyer la toucheF2et puisles touchesCtrl+Shift+Enteren même temps. Par suite la matrice inverse s’affiche dans le diapason de cellules réservé B6:E9 (fig.6.37).

Fig. 6.37
Pour obtenir les valeurs des inconnues il faut multiplier la matrice inverse par le vecteur colonne b. Pour faire ça il faut:
– sélectionner les cellules H6:H9pour le résultat;
– cliquer sur sur l’icône fx en passant à premier pas d’assistant formule;
– cliquer sur la catégorie Ìàòåìàòè÷åñêèåde la boîtequi s’affiche et dans la case déroulante de cette boîte cliquer sur le nom ÌÓÌÍÎÆ et puis sur le boutonOK de cette boîte en passant à deuxiéme pas. Il faut tenir compte que la multiplication d’une matrice A par matrice Best possiblequand le nombre de colonnes de la matrice Aest égale au nombre de lignes de la matrice B. Bien plus il faut avoir en vue que ÀÂ≠ ÂÀ;
–sélectionner la plage B6:E9qui comprend les valeurs de la matriceA.Cette action provoque l’apparition la plage de cellulesB6:E9dans premièrecase Ìàññèâ1 (fig. 6.38);
– sélectionner la plageG1:G4 qui comprend les valeurs de vecteurcolonneb.Cette action provoque l’apparition la plage de cellulesG1:G4 dans la deuzièmecase Ìàññèâ 2;
–cliquer sur le bouton OKde cetteboîte.
– cliquer sur la catégorie Ìàòåìàòè÷åñêèåde la boîtequi s’affiche et dans la case déroulante de cette boîte cliquer sur le nom ÌÓÌÍÎÆ et puis sur le boutonOK de cette boîte en passant à deuxiéme pas.
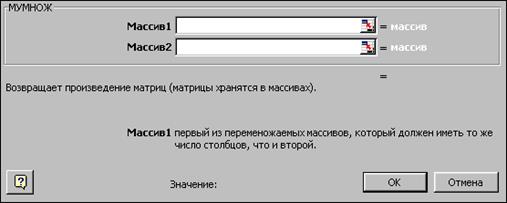
Fig. 6.38
Premier nombre de vecteur x est apparue dans la première cellule du diapason réservé pour résultat. Pour obtenir toutes les valeurs de la vecteur x il faut appuyer la touche F2et puis les touches Ctrl+Shift+Enter en même temps. Toutes les valeurs de vecteur colonne x s’affichent dans les cellules H6:H9.
Pour vérifier la corection du résultat obtenu il faut multiplier la matrice A par vecteur x. Le résultat obtenu doit correspondre au vecteur b.Cette opérations’effectue à l’aide de fonction ÌÓÌÍÎÆ(Â1:Å4;Í6:Í9)de la manière écrite au–dessus.
Par suite la feuille de calcul prendra la forme présentée sur la fig.6.39.

Fig. 6.39
Exemple 2.
Il faut résoudre le système des équations examiné dans l’exemple 1 par la méthode de Cramer.
Avant d’aborder cet problème il faut faire les actions préparatoires:
– faire entrer la manrice A et vecteur b dans la feuille de travail;
– former quatre matrices auxiliaires en changeant successivement les colonnes de la matrice A par le vecteur colonne b;
– reserver les cellules I10:I15 pour déterminants d,d1,d2,d3,d4 (fig.6.40).
Après ces actions on calcule le déterminant principal de la matrice A. Pour cela il faut:
– placer le pointeur dans la cellule I10;
– cliquer sur la catégorie Ìàòåìàòè÷åñêèå de la boîte qui s’affiche et dans la case déroulante de cette boîte cliquer sur le nom ÌÎÏÐÅÄ et puis sur le bouton OK;
– sélectionner la plage B1:E4qui comprend les valeurs de la matriceA.Cette action provoque l’apparition la plage de cellulesB1:E4dans premièrecase Ìàññèâ1;
– cliquer sur le bouton OK.
La valeur de déterminantde la matriceAs’affiche dans la cellule I10.
Pour calculer des déterminants auxiliairs il faut créer les formules dans les cellules I11, I12, I13, I14 :
I11=ÌÎÏÐÅÄ(B6:E9), I12=ÌÎÏÐÅÄ(B11:E14),
I13=ÌÎÏÐÅÄ(B16:E19), I14=ÌÎÏÐÅÄ(B21:E24)
et réaliser ces dernieres. Dans les cellules I11, I12, I13, I14 les valeurs de déterminants auxiliairs s’affichent (fig.6.40).
En utilisant des formules de Cramer on calcul les valeurs des inconnues x. Avec cela on divise successivement les déterminants auxiliairs par le déterminant principal de la matrice A. Cette action peut être réalisée par la formule =I11/$I$10 créé dans la cellule K11. Pour obtenir les autre valeurs de x il faut copier cette formule dans les cellules K12, K13 et K14. De telle maniére le système des équation est résolu.

Fig. 6.40
Exemple 3.
Calculer la matrice Cpar la formule C=A2+2AB, où
 .
.
Cette formule peut être calculée en quelques étapes. L’ordre de la résolution.
– faire entrer de données de départ (matrice A, B) dans la feulle de calcul (fig.6.41);
– réserver les cellules B5:D7pour le produit des matricesAetB;
–utiliser la fonctionÌÓÌÍÎÆ (B1:D3;G1:I3)par la méthode écrivée;
– réserver les cellules J5:I7pour le produit des matricesA2=A*A;
– utiliser la fonctionÌÓÌÍÎÆ(B1:D3;B1:I3)pourobtenir le résultat de calcul A2=A*A;
– réserver les cellules B9:D11pour le produit 2AB;
– créer la formule =2*B5:D7dans la celluleB9et la réaliser;
– copier cette formule successivement dans les cellules restantes;
– réserver les cellules G9:I11 pour le résultat C = A2 + 2AB;
– créer la formule =G5:I7 + 2*B9:D11dans la celluleG9et la réaliser;
– copier cette formule successivement dans les cellules restantes;
En outre il y a méthode plus facile de la résolution ce problème. Pour cela il faut:
– réserver les cellules E14:G16(fig.6.41);
– créer la formule =ÌÓÌÍÎÆ(B1:D3;B1:D3)+2*ÌÓÌÍÎÆ(B1:D3;G1:I3)dans la celluleE14et la réaliser;
– copier cette formule successivement dans les cellules restantes.
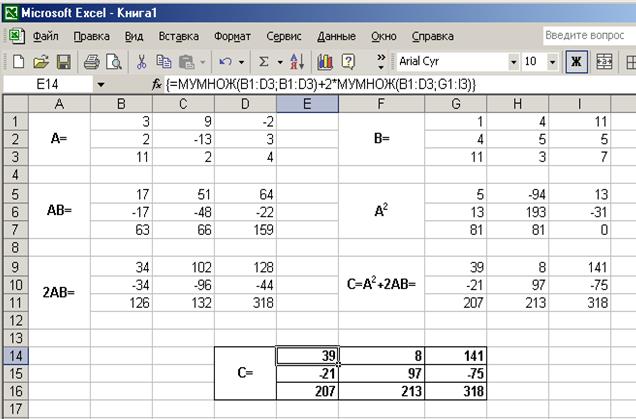
Fig. 6.41
6.2.14.2. Énoncé du problème
Il faut:
1. résoudre le système d’équations par la méthode de Cramer;
2. résoudre le système d’équations par la méthode de matrice inverse;
3. vérifier la solution obtenue pour chaque système d’équations;
4. faire les actions indiqueées avec matrices;
Variantes
Variante ¹1
1)  2)
2) 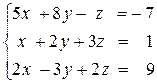
3) 2 (A + B) (2B – A), 
Variante ¹2
1)  2)
2) 
3) 3 A - (A + 2B) B, 
Variante ¹3
1)  2)
2) 
3) 2(A–B)(A2 + B), 
Variante ¹ 4
1)  2)
2) 
3) (A2 – B2)(A + B), 
Variante ¹ 5
1)  2)
2) 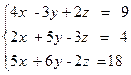
3) (A–B2)(2A+B), 
Variante ¹ 6
1)  2)
2) 
3) (A – B) A + 2B, 
Variante ¹ 7
1)  2)
2) 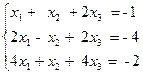
3) 2(A–0,5B)+AB, 
Variante ¹ 8
1) 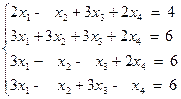 2)
2) 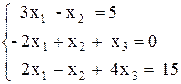
3) (A – B)A + 3B, 
Variante ¹ 9
1)  2)
2) 
3) 2A – (A2 + B) B, 
Variante ¹ 10
1)  2)
2) 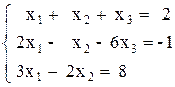
3) 3 (A2 – B2) –2ÀB, 
Variante ¹ 11
1)  2)
2) 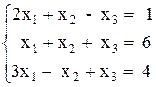
3) (2A–B)(3À+B)–2ÀÂ, 
Variante ¹ 12
1)  2)
2) 
3) À(A2–B)-2(B+À)Â, 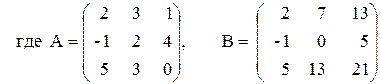
Variante ¹ 13
1)  2)
2) 
3) (A+B)A–B(2À+3Â), 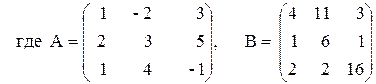
Variante ¹ 14
1)  2)
2) 
3) A(2A+B)–B(À–Â), 
Variante ¹ 15
1)  2)
2) 
3) 3(A+B)(A–2À), 
Variante ¹ 16
 2)
2) 
3)  ãäå
ãäå 
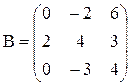
Variante ¹ 17
1)  2)
2) 
3) 2À + 3B(ÀB-2À), 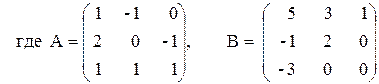
Variante ¹ 18
1)  2)
2) 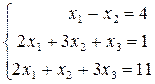
3) 
Variante ¹ 19
1)  2)
2) 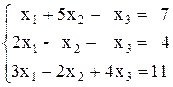
3) 2A - ÀB(Â - À) + Â, 
Variante ¹ 20
1)  2)
2) 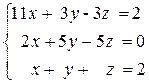
3) A2 - (A + B)–(À – 3Â), 
Variante ¹ 21
1)  2)
2) 
3) 
Variante ¹ 22

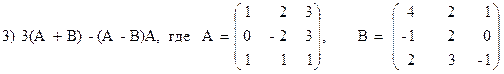
Variante ¹ 23
1)  2)
2) 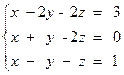
3) À(A - B) + 2Â(A + Â), 
Variante ¹ 24
1) 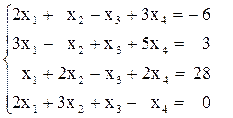 2)
2) 

Variante ¹ 25


Variante ¹ 26


Variante ¹ 27


Variante ¹ 28
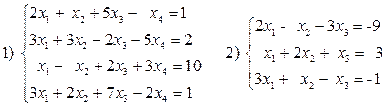

Variante ¹ 29

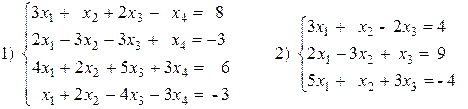

Variante ¹ 30


6.2.14.4 Questions de contrôle
1. Quele sens de méthode de matrice inverse et de méthode de Cramer?
2. Énumerez la succession des opérations nécessaires pour calculer la matrice inverse.
3. Énumerez la succession des opérations nécessaires pour calculer un déterminant.
4. En quelle catégorie se trouve la fonction ÌÎÁÐ( )?
5. Décrivez la succession des opérations qui permet de multiplier un nombre par une matrice.
Date: 2015-12-24; view: 821
| <== previous page | | | next page ==> |
| Travail pratique N 11 | | | Travail pratique ¹ 15 |