
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
TRAVAIL PRATIQUE N16
Thème : programmation avec l`utilisation des guide-classes.
But du travail : réception de l`expérience de la programmation avec l`utilisation des guide-classes.
Devoir
Il faut élaborer un organigramme et composer un programme pour l`exécution des actions indiquées dans le tableau 5.11 avec des éléments d`une matrice 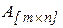 en utilisant les guide - classes créées d`avance. Les éléments de la matrice A peuvent être pris de n`import quel type à valeurs arbitraires.
en utilisant les guide - classes créées d`avance. Les éléments de la matrice A peuvent être pris de n`import quel type à valeurs arbitraires.
Le guide-classe doit avoir les fonctions suivantes :
- fonction pour faire entrer une matrice d`un fichier externe ;
- fonction pour l`exécution des actions indiquées dans le tab. 5.11 ;
- fonction pour afficher une matrice sur l`écran ;
- fonction pour afficher une série de nombres sur l`écran ( pour les variantes, qui ont comme résultat un vecteur de nombres ).
Il faut créer d`avance le nombre nécessaire des fichiers externes avec des données de départ.
Il faut vérifier le fonctionnement correct de la matrice par trois-quatre exemplaires des données du type indiqués dans le tab. 5.13.
Pour les variantes du tab. 5.13 dont le type complexe des données n`est pas indiqué il faut vérifier le fonctionnement du programme avec ce type de données.
L`affichage de l`information sur l`écran doit être fait sous forme suivante :
PROGRAMMATION AVEC L`UTILISATION DES GUIDE-CLASSES
Matrice de départ
. . . . . . . . . . . . . . .
Résultat du calcul
. . . . . . . . . . . . . . .
Matrice de départ
. . . . . . . . . . . . . . .
Résultat du calcul
. . . . . . . . . . . . . . .
Matrice de départ
. . . . . . . . . . . . . . .
Résultat du calcul
. . . . . . . . . . . . . . .
5.16.2 Généralités et recommandations pour l`exécution du travail
L`utilisation des guide-classes permet de créer des classes paramétrisées ( guide-classe ). Une telle sorte de la classe crée la famile des classes de parenté, qui peuvent être appliquées avec n`importe quel type de paramètre.
La syntaxe de la déclaration du guide-classe a la forme suivante :
template < class T >
class A
{
// corps de classe
}
T est le type fictif des données. Le nom de ce type est choisi par le programmeur. Ce nom est changé automatiquement par le compilateur. Des données avec lesquelles l`objet fonctionera sont créées sur la base de cette classe. Le T peut être présenté par la liste des données. Dans ce cas toutes les données doivent être écrites séparément . La séparation est faite par la virgule.
Les fonction – membres du guide-classe devient automatiquement les guide-fonctions. Si cette fonction est définie hors du guide-classe, sa tête doit avoir la forme suivante :
template < liste des paramètres du guide-classe >
Y < paramètre de guide > :: X ( liste des paramètres )
{
// corps de la fonction
}
où Y est le type du résultat qui donne la classe , X est le nom de la fonction. La déclaration des paramètres de guide dans la tête de la fonction doit correspondre à la déclaration du guide-classe. Avec cela, les noms des paramètres de la fonction et du guide-classe ne peuvent pas coïncider.
Le guide-classe peut hériter l`autre guide-classe de telle manière que des classes ordinaires. Bien plus le guide-classe peut être utilisé comme la classe de base par l`autre guide-classe ainsi que par l`autre classe ordinaire.
La première compilation fait l`instanciation du guide-classe de la manière analogue que le guide-fonction. Chaque vérsion de la fonction ou de la classe qui est créée d`après le guide, comprend le même code de base, mais il y a une différence qui consiste en liste des paramètres.
L`efficacité de la vérsion créée pour de différents types des données peut différer assez bien. S`il existe l`algorithme plus efficace pour certains types des données on peut soit prévoir l`utilisation des certaines fonction-membres soit completment redéfinir ( spécialiser ) le guide-classe.
Pour la spécialisation de la fonction-membre il faut déterminer la variante de son code en présentant dans sa tête le type des données concretes. Par exemple, la tête de la fonction – membre généralisée entr_matr ( ) du guide-classe member a la forme suivante :
template < class type >
void member < type >:: entr_matr ( )
{
// corps de la fonction spécialisée
}
Si le guide-classe member a été créé avec le type complex , la variante correspondante de la fonction-membre destinée à faire entrer une matrice ainsi que la fonction-membre qui assure la réalisation des actions avec une matrice déstinée à traiter des nombres complexes est créé automatiquement.
Lors de la spécialisation d`une classe, il faut placer la déclaration de la classe spécialisée après la déclaration de la variante généralisée de classe . Des guides représentent le moyen puissant et effectif du traitement des données de différents types . Ce phénomène est appelé polymorphisme paramètrique. En plus, des guides assurent une grande fiabilité du fonctionnement des programmes.
5.16.3 Questions de contrôle et devoirs
1. Quelle est la nécessité de créer la classe paramétrisée ?
2. Donnez la syntaxe de la définition d`une fonction-membre qui se trouve en intérieur du guide-classe et hors de lui.
3. Pour quel but spécialise-t-on la fonction-membre de la classe et la classe même?
4. Quels sont les avantages et les inconvéniants d`utilisation des guides ?
Annexe 1
Les fonctions principales de la bibliothèque des fonctions mathematiques
standardisées pour le traitement des nombres réels ( le fichier math.h )
| Fonction | Destination | Argument | Résultat | ||
| Type | Unité de mesure | Type | Unité de mesure | ||
| abs(x) | 
| Int | int | ||
| labs(x) | long int | long int | |||
| fabs(x) | Double | double | |||
| fabsl(x) | long double | long double | |||
| sin(x) | 
| Double | radian | double | |
| sinl(x) | long double | radian | long double | ||
| cos(x) | 
| Double | radian | double | |
| cosl(x) | long double | radian | long double | ||
| tan(x) | 
| Double | radian | double | |
| tanl(x) | long double | radian | long double | ||
| asin(x) | 
| Double | double | radian | |
| asinl(x) | long double | long double | radian | ||
| acos(x) | 
| Double | double | radian | |
| acosl(x) | long double | long double | radian | ||
| atan(x) | 
| Double | double | radian 
| |
| atanl(x) | long double | long double | |||
| Atan2(x, y) | 
| double, double | double | radian 
| |
| Atan2l(x, y) | long double, long double | long double | |||
| sinh(x) | 
| Double | double | ||
| sinhl(x) | long double | long double | |||
| cosh(x) | 
| Double | double | ||
| coshl(x) | long double | long double | |||
| tanh(x) | 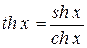
| Double | double | ||
| tanhl(x) | long double | long double | |||
| ceil(x) | arrondissement jusqu`au nombre entier plus proche et plus grand | Double | double | nombre entier | |
| ceill(x) | long double | long double |
| Fonction | Destination | Argument | Résultat | ||
| Type | Unité de mesure | Type | Unité de mesure | ||
| floor(x) | arrondissement jusqu`au nombre entier plus proche et plus petit | Double | double | nombre entier | |
| floorl(x) | long double | long double | |||
| log(x) | 
| Double | double | ||
| logl(x) | long double | long double | |||
| Log10(x) |

| Double | double | ||
| Log10l(x) | long double | long double | |||
| sqrt(x) | 
| Double | double | ||
| sqrtl(x) | long double | long double | |||
| exp(x) | 
| Double | double | ||
| expl(x) | long double | long double | |||
| pow10(x) | 
| Int | double | ||
| Pow10l(x) | Int | long double | |||
| pow(x, y) | 
| double, double | nombre entier en diapason 
| double | |
| powl(x, y) | long double, long double | long double | |||
| hypot(x, y) | 
| double, double | double | ||
| hypotl(x, y) | long double, long double | long double | |||
| fmod(x, y) | reste après la division  par par 
| double, double | double | nombre entier | |
| fmodl(x, y) | long double, long double | long double | |||
| Modf(x, &xc) | retourne la partie fractionnée de 
| double, double | double | valeur de la partie entiere est disposée dans la variable 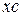
| |
| Modfl(x, &xc) | long double, long double | long double | |||
| Frexp(x, &n) | retourne tel  , que , que 
| double, double | double | valeur de la puissance est disposée dans la variable 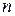
| |
| frexpl(x, &n) | long double, long double | long double | |||
| ldexp(x, n) | 
| double, int | double | ||
| ldexpl(x, n) | long double, int | long double |
| Fonction | Destination | Argument | Résultat | ||
| Type | Unité de mesure | Type | Unité de mesure | ||
| Poly(x,n,c) | 
| double, int, double[ ] | 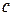 – tableau à dimension [n+1] – tableau à dimension [n+1]
| double | |
| polyl(x, n, c) | long double, int, long double | long double | |||
| Atof(&s[ ]) | transforme une ligne des caractères en un nombre | char | Const | double | |
| _atold(&s[ ]) | char | long double |
Annexe 2
Les fonctions principales de la bibliothèque des fonctions mathematiques standardisées pour le traitement des nombres complexes ( le fichier complex.h)
| Fonction | Destination | Type | |
| de l`argument | du résultat | ||
| real(z) | 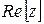
| complex | double |
| imag(z) | 
| complex | double |
| abs(z) | 
| complex | double |
| arg(z) | 
| complex | double |
| norm(z) | 
| complex | double |
| conj(z) | nombre complexe conjugué | complex | complex |
| sin(z) | 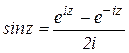
| complex | complex |
| cos(z) | 
| complex | complex |
| tan(z) | complex | complex | |
| asin(z) | 
| complex | complex |
| acos(z) | 
| complex | complex |
| atan(z) | 
| complex | complex |
| sinh(z) | 
| complex | complex |
| cosh(z) | 
| complex | complex |
| tanh(z) | complex | complex | |
| log(z) | 
| complex | complex |
| log10(z) | 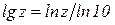
| complex | complex |
| exp(z) | 
| complex | complex |
| sqrt(z) | 
| complex | complex |
| pow(x, y) | 
| complex, complex | complex |
| pow(x, y) | complex, double | complex | |
| pow(x, y) | double, double | complex | |
| polar(m, a) | présentation d`un nombre complexe sous forme de puissance 
| double, double | complex |
Date: 2015-12-24; view: 1182
| <== previous page | | | next page ==> |
| TRAVAIL PRATIQUE N15 | | | STUCTURE ET PRINCIPE DU FONTIONNEMENT |