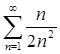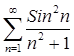Tests for convergence and divergence of series of constants.

Series. Exercises.

Def 1. The expression

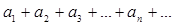
or shortly

, or , or (1)

(where is a sequence of real numbers) is called a series of numbers.

Def 2. The expression

(2)

is called n-th partial sum.

( I.e. …)

Def 3. If the sequence of partial sums converges, i.e. if there exists a number S such that 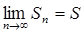, the series (1) is called convergent and S is called its sum. If does not exist, the series is called divergent.

Example 1.

(it is well known formula for the sum of the first n terms of geometrical progression). Since 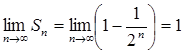, the series is convergent and has sum S=1. So, .

Example 2. . Here or 1 according as is even or odd. Hence does not exist and the series is divergent.

Special series.

1. Geometric series: …. where and are constants, converges to if <1 and diverges if .

2. The series: … , where is a constant , converges for >1 and diverges for .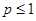

The series with is called the harmonic series.

3. Telescoping series: For such series it is possible to obtain an explicit expression for the general n-th partial sum, from which the infinite limit can be more easily evaluated. For example, . The n-th term can be expressed as , then partial sum

and from this .

Tests for convergence and divergence of series of constants.

Theorem. ( The necessary condition for convergence).

If the series is convergent, then .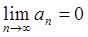

Corollary. ( The Test for Divergence)

If does not exist or then the series is divergent.

Example 1. The series 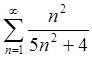is divergent, since

Example 2. The series is divergent, since does not exist.

Properties of Convergent Series

1. = C ( where C any constant)

2. +

Tests for convergence and divergence of series of constants.

1. Comparison test for series of nonnegative terms.

Let for all . Then

(a) if converges , also converges;

(b) if diverges, also diverges.

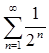Example. (a) Since and converges, also converges.

(b) Since and diverges, also diverges.

2. Limit comparison test for series of positive terms.

Let and for all .

(a) If , where , then and either both converge or both diverge.

(b) If l=0 in (a) and converges, then converges.

(c) If l = ¥ in (a) and diverges, then diverges.

This test permits us to conveniently obtain as a corollary the following theorem about p series.

Theorem 1.Let . Then:

1) converges if and A is finite.

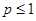2) diverges if and A¹0 (A may be infinite).

In fact in the Theorem 1we compare our series with p-series , since (see limit comparison test (a) ).

Example. converges, since .

3. Ratio test: Let . Then the series

i) converges if ,

ii)diverges if .

If the test fails.

4. The n-th root test : Let . Then the series

i) converges if ,

ii)diverges if .

If the test fails.

The Integral Test.

Theorem. Suppose f is continuous, positive, decreasing function on [0, ¥) and let 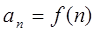. Then the series is convergent if and only if exists limit : 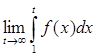. In other words:

i) if exists limit 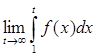then is convergent.

ii) if limit 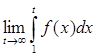does not exist, then is divergent.

Note: The limit 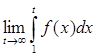is denoted and is called improperintegral. By the Newton-Leibnitz’s formula

where F(t) - any antiderivative for f(t).

Exercises

Test the convergence of the following series

Date: 2015-12-24; view: 1662