
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
CARACTERÍSTICAS DE VACIO
Se hace la prueba como si fuera una maquina separadamente excitada.
Se encuentra una función  a velocidad
a velocidad  constante.
constante.
La característica de vacío se ha tratado en el apartado que su forma depende de las dimensiones de las distintas partes del circuito magnético y de los materiales usados
La f.e.m. generada en el inducido viene dado por la ecuación


Fig. 1. Ensayo en característica de vacío

Fig. 2. Curva de saturación de un generador de excitación independiente
Datos obtenidos en la práctica:
de 0 a 10 de 10 a 0
| I | V | I | V | |
| 0.81 | 19.3 | 9.21 | 155.4 | |
| 0.9 | 20.8 | 8.84 | ||
| 1.04 | 23.4 | 7.65 | ||
| 2.02 | 45.0 | 6.89 | 136.7 | |
| 4.54 | 95.1 | 6.26 | 128.2 | |
| 5.98 | 120.4 | 4.24 | 92.3 | |
| 7.08 | 138.1 | 3.22 | 72.8 | |
| 8.4 | 150.6 | 2.34 | 54.9 | |
| 9.21 | 155.4 | 1.81 | 42.9 | |
Éstos datos podemos procesarlos y graficarlos con ayuda de MATLAB y análisis numérico básico para visualizar las curvas de vacío.
Usamos una herramienta llamada trazador cúbico natural para poder graficar los puntos obtenidos en la práctica.
El algoritmo del trazador cúbico natural:
-----------------------------------------------------------------------------------------------------
%trazador cubico natural
function[a,b,c,d]=trazadornatural(x,y,z)
n=length(x);
clear A B C D;
if n<4
return
end
for i=1:n-1
h(i)=x(i+1)-x(i);
end
s(1)=0;
s(n)=0;
B(1)=2*(h(1)+h(2));
C(1)=h(2);
D(1)=6*((y(3)-y(2))/h(2)-(y(2)-y(1))/h(1))-h(1)*s(1);
for i=2:n-3
A(i)=h(i);
B(i)=2*(h(i)+h(i+1));
C(i)=h(i+1);
D(i)=6*((y(i+2)-y(i+1))/h(i+1)-(y(i+1)-y(i))/h(i));
end
A(n-2)=h(n-2);
B(n-2)=2*(h(n-2)+h(n-1));
D(n-2)=6*((y(n)-y(n-1))/h(n-1)-(y(n-1)-y(n-2))/h(n-2))-h(n-1)*s(n);
u=tridiagonal(A,B,C,D);
%fprintf('s(n+1) ===> s(n-1)\nalgoritmo de thomas\n');
%%disp(u');
for i=2:n-1
s(i)=u(i-1);
end
for i=1:n-1
a(i)=(s(i+1)-s(i))/(6*h(i));
b(i)=s(i)/2;
c(i)=(y(i+1)-y(i))/h(i)-(2*h(i)*s(i)+h(i)*s(i+1))/6;
d(i)=y(i);
end
%matr=[a' b' c' d'];
%fprintf(' a(i) b(i) c(i) d(i)\n');
%disp(matr);
%fprintf('\n\n');
fprintf('calculando los polinomios....\n\n');
syms xt p_t %% obtencion de los polinomios
for i=1:n-1
fprintf('p(t) en %d<=xt<=%d ; ',x(i),x(i+1));
p_t=a(i)*(xt-x(i))^3+b(i)*(xt-x(i))^2+c(i)*(xt-x(i))+d(i);
disp(p_t);
fprintf('\n');
end
if nargin==3
p=[];
m=length(z);
for k=1:m
t=z(k);
for i=1:n-1
if t>=x(i) & t<=x(i+1)
p(k)=a(i)*(t-x(i))^3+b(i)*(t-x(i))^2+c(i)*(t-x(i))+d(i);
end
end
end
if m>1
k=m; i=n-1;
p(k)=a(i)*(t-x(i))^3+b(i)*(t-x(i))^2+c(i)*(t-x(i))+d(i);
end
clear a b c d;
a=p;
end
-----------------------------------------------------------------------------------------------------
Para poder usar este algoritmo, hacemos una función en MATLAB y después solo insertar los datos de la práctica, también hay que tener en cuenta cómo usar la función de trazado cúbico natural, dado que al ingresar datos para la primera curva, debemos borrar los datos para la siguiente inserción de datos, ésto es más conocimiento de programación.
Inserción de datos y convocación de función para trazado cúbico:
-------------------------------------------------------------------------------------------------------
hold on;
grid on;
%%de 1 a 10 A%%
I1=[0.81 0.90 1.04 2.02 4.54 5.980 7.080 8.400 9.210];
E1=[19.3 20.8 23.4 45.0 95.1 120.4 138.1 150.6 155.4];
Intervalo=[0.81:0.01:9.21];
p=trazadornatural(I1,E1,Intervalo);
plot(I1,E1,'o');
plot(Intervalo,p,'b'); %%grafica 1 color verde
%%de 10 a 1 A%%
I2=[1.81 2.34 3.22 4.24 6.260 6.890 7.650 8.840 9.210];
E2=[42.9 54.9 72.8 92.3 128.2 136.7 145.0 154.0 155.4];
Intervalo=[1.81:0.01:8.84];
p=trazadornatural(I2,E2,Intervalo);
plot(I2,E2,'o');
plot(Intervalo,p,'r');%%grafica 2 color rojo
xlabel('I exc[A]','FontSize',12);
ylabel('E o[V]','FontSize',12);
-----------------------------------------------------------------------------------------------------
Los resultados en la consola de MATLAB son:
----------------------------------------------------------------------------------
a(i) b(i) c(i) d(i)
40.8540 0 16.3357 19.3000
-15.3753 11.0306 17.3285 20.8000
-2.0342 4.5729 19.5130 23.4000
0.1281 -1.4077 22.6150 45.0000
0.1167 -0.4394 17.9603 95.1000
-1.1576 0.0646 17.4205 120.4000
0.6120 -3.7555 13.3606 138.1000
0.5481 -1.3319 6.6452 150.6000
calculando los polinomios....
p(xt) en 8.100000e-001<=xt<=9.000000e-001 ; (2299052265710409*xt)/140737488355328 + (1437424080608791*(xt - 81/100)^3)/35184372088832 + 85400119003239911/14073748835532800
p(xt) en 9.000000e-001<=xt<=1.040000e+000 ; (4877539772691167*xt)/281474976710656 + (6209672028229975*(xt - 9/10)^2)/562949953421312 - (8655550004163413*(xt - 9/10)^3)/562949953421312 + 2929787440319189/562949953421312
p(xt) en 1.040000e+000<=xt<=2.020000e+000 ; (5492420686520959*xt)/281474976710656 + (2574341026481341*(xt - 26/25)^2)/562949953421312 - (286291923835259*(xt - 26/25)^3)/140737488355328 + 10929961763094413/3518437208883200
p(xt) en 2.020000e+000<=xt<=4.540000e+000 ; (6365546310564377*xt)/281474976710656 - (1584903995642609*(xt - 101/50)^2)/1125899906842624 + (72100596845773*(xt - 101/50)^3)/562949953421312 - 9601479768026077/14073748835532800
p(xt) en 4.540000e+000<=xt<=5.980000e+000 ; (5055368721368785*xt)/281474976710656 - (7915887541352339*(xt - 227/50)^2)/18014398509481984 + (4203562600667125*(xt - 227/50)^3)/36028797018963968 + 38168962901691017/2814749767106560
p(xt) en 5.980000e+000<=xt<=7.080000e+000 ; (153232716387511*xt)/8796093022208 + (581903838044327*(xt - 299/50)^2)/9007199254740992 - (1303344156086639*(xt - 299/50)^3)/1125899906842624 + 7135897793826371/439804651110400
p(xt) en 7.080000e+000<=xt<=8.400000e+000 ; (7521335983234551*xt)/562949953421312 - (2114148867665183*(xt - 177/25)^2)/562949953421312 + (5512451699617427*(xt - 177/25)^3)/9007199254740992 + 612308245154564153/14073748835532800
p(xt) en 8.400000e+000<=xt<=9.210000e+000 ; (3740900942863481*xt)/562949953421312 - (5998536576078957*(xt - 42/5)^2)/4503599627370496 + (4937067140805723*(xt - 42/5)^3)/9007199254740992 + 133391737662990867/1407374883553280
a(i) b(i) c(i) d(i)
-1.4454 0 23.0475 42.9000
0.6894 -2.2982 21.8295 54.9000
0.2107 -0.4782 19.3862 72.8000
-0.4000 0.1665 19.0683 92.3000
0.1773 -2.2577 14.8440 128.2000
0.2974 -1.9226 12.2104 136.7000
-0.5364 -1.2445 9.8035 145.0000
2.8462 -3.1592 4.5631 154.0000
calculando los polinomios....
p(xt) en 1.810000e+000<=xt<=2.340000e+000 ; (1621825651890461*xt)/70368744177664 - (3254802903331163*(xt - 181/100)^3)/2251799813685248 + 8331469530005119/7036874417766400
p(xt) en 2.340000e+000<=xt<=3.220000e+000 ; (3072224903366099*xt)/140737488355328 - (5175136616296547*(xt - 117/50)^2)/2251799813685248 + (6209592301554833*(xt - 117/50)^3)/9007199254740992 + 26874091841541777/7036874417766400
p(xt) en 3.220000e+000<=xt<=4.240000e+000 ; (5456736152239839*xt)/281474976710656 - (8614445578162845*(xt - 161/50)^2)/18014398509481984 + (7590414124662891*(xt - 161/50)^3)/36028797018963968 + 146034394716173761/14073748835532800
p(xt) en 4.240000e+000<=xt<=6.260000e+000 ; (5367238203856975*xt)/281474976710656 + (749722008142845*(xt - 106/25)^2)/4503599627370496 - (1801546078292011*(xt - 106/25)^3)/4503599627370496 + 8057625915099937/703687441776640
p(xt) en 6.260000e+000<=xt<=6.890000e+000 ; (4178225145063783*xt)/281474976710656 - (2541911806576685*(xt - 313/50)^2)/1125899906842624 + (99794515894727*(xt - 313/50)^3)/562949953421312 + 496470130310340881/14073748835532800
p(xt) en 6.890000e+000<=xt<=7.650000e+000 ; (6873871182060107*xt)/562949953421312 - (2164688536494617*(xt - 689/100)^2)/1125899906842624 + (5358256624205897*(xt - 689/100)^3)/18014398509481984 + 2959428618829921317/56294995342131200
p(xt) en 7.650000e+000<=xt<=8.840000e+000 ; (2759428745262473*xt)/281474976710656 - (350284241886319*(xt - 153/20)^2)/281474976710656 - (4831029504633747*(xt - 153/20)^3)/9007199254740992 + 394084834435744031/5629499534213120
p(xt) en 8.840000e+000<=xt<=9.210000e+000 ; (1284387791931299*xt)/281474976710656 - (7113967767976169*(xt - 221/25)^2)/2251799813685248 + (6408979971149685*(xt - 221/25)^3)/2251799813685248 + 799828958319208521/7036874417766400
-------------------------------------------------------------------------------------------------------
Gráfica de las curvas:

Fig. 3. La curva verde es la curva de 1 a 10, la roja es la de 10 a 1
Curva de saturación
Para la curva de saturación hacemos un promedio de los datos que obtenemos en las gráficas, así mismo, procedemos a usar el trazador cúbico, para la parte lineal, es decir la recta del entrehierro usamos regresión lineal simple para obtener dicha recta
----------------------------------------------------------------------------------------------
figure
hold on;
grid on;
I3=(I1+I2)./2; %%promedio de las corrientes
E3=(E1+E2)./2; %%promedio de los voltajes
Intervalo=[min(I3):0.01:max(I3)];
p=trazadornatural(I3,E3,Intervalo);
plot(I3,E3,'x');
plot(Intervalo,p,'g');%%grafica 3 verde
%%regresion lineal simple...
x=[];
y=[];
for i=1:4
x(1,i)=I3(1,i);
y(1,i)=E3(1,i);
end
%%%%%%%%%%%%%%datos estadisticos
xx=x.^2;
yy=y.^2;
xy=x.*y;
Sx=sum(x);
Sy=sum(y);
Sxy=sum(xy);
Sxx=sum(xx);
Syy=sum(yy);
%%%%%%%%%%%%%%%
n=4; %% ver la grafica, hasta donde es lineal la curva de saturación
%%regresion lineal
B1=(Sx*Sy-n*Sxy)/((Sx)^2-n*Sxx);
B0=(Sy-B1*Sx)/(n);
x1=[0:0.1:10];
y1=B0+B1.*x1;
plot(x1,y1,'y'); %%recta del entrehierro
----------------------------------------------------------------------------------------------
Grafica de la curva se saturación y recta del entre-hierro

Las funciones estimadas son las siguientes:
Parte curva:
p(xt) en 3.130000e+000<=xt<=5.400000e+000 ; (5781280943589713*xt)/281474976710656 - (1436106427805571*(xt - 313/100)^2)/2251799813685248 - (4161350027027495*(xt - 313/100)^3)/144115188075855872 + 122784779775073271/28147497671065600
p(xt) en 5.400000e+000<=xt<=6.435000e+000 ; (1210161961812469*xt)/70368744177664 - (3757800158237931*(xt - 27/5)^2)/4503599627370496 - (22408922908419*(xt - 27/5)^3)/4503599627370496 + 1321795693648853/70368744177664
p(xt) en 6.435000e+000<=xt<=7.365000e+000 ; (8699963029139723*xt)/562949953421312 - (956844965967143*(xt - 1287/200)^2)/1125899906842624 - (7137698650532409*(xt - 1287/200)^3)/9007199254740992 + 3276590883959108019/112589990684262400
p(xt) en 7.365000e+000<=xt<=8.620000e+000 ; (6652585542756753*xt)/562949953421312 - (107691167823135*(xt - 1473/200)^2)/35184372088832 + (6743956576339301*(xt - 1473/200)^3)/18014398509481984 + 6137854676876645551/112589990684262400
p(xt) en 8.620000e+000<=xt<=9.210000e+000 ; (3323511387352975*xt)/562949953421312 - (7436720353881909*(xt - 431/50)^2)/4503599627370496 + (8403073846194249*(xt - 431/50)^3)/9007199254740992 + 570886097470831731/5629499534213120
Parte recta
y1=B0+B1.*x1; B0=4.3367 ; B1= 20.5560;
Al final nos queda:

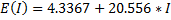










En código matlab:
------------------------------------------------------------------------------------------------------------------------
figure
hold on
grid on
x=[0:0.01:3.13];
B0=4.3367;
B1=20.5560;
y=B0+B1.*x;
plot(x,y)
x=[3.13:0.01:5.4];
y=(5781280943589713.*x)./281474976710656 - (1436106427805571.*(x - 313/100).^2)./2251799813685248 - (4161350027027495.*(x - 313/100).^3)./144115188075855872 + 122784779775073271/28147497671065600;
plot(x,y)
x=[5.4:0.01:6.435];
y=(1210161961812469.*x)./70368744177664 - (3757800158237931.*(x - 27/5).^2)./4503599627370496 - (22408922908419.*(x - 27/5).^3)./4503599627370496 + 1321795693648853/70368744177664;
plot(x,y)
x=[6.435:0.01:7.265];
y=(8699963029139723.*x)./562949953421312 - (956844965967143.*(x - 1287/200).^2)./1125899906842624 - (7137698650532409.*(x - 1287/200).^3)./9007199254740992 + 3276590883959108019/112589990684262400;
plot(x,y)
x=[7.265:0.01:8.62];
y=(6652585542756753.*x)./562949953421312 - (107691167823135.*(x - 1473/200).^2)./35184372088832 + (6743956576339301.*(x - 1473/200).^3)./18014398509481984 + 6137854676876645551/112589990684262400;
plot(x,y)
x=[8.62:0.01:9.21];
y=(3323511387352975.*x)./562949953421312 - (7436720353881909.*(x - 431/50).^2)./4503599627370496 + (8403073846194249.*(x - 431/50).^3)./9007199254740992 + 570886097470831731/5629499534213120;
plot(x,y)
------------------------------------------------------------------------------------------------------------------------
Gráfica:

Date: 2015-12-24; view: 1165
| <== previous page | | | next page ==> |
| Der hinterhältige Nagel | | | Die Deutschen in ihr Urlaub |