
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Integration of simple rational fractions. Integration of rational fractions. Integration of expressions containing trigonometric functions. Integration of irrational functions
Theoretical questions:
1. Integration of rational fractions. 2. Integration of expressions containing trigonometric functions. 3. Integration of irrational functions.
Classroom assignments:
1. Calculate integrals:
1.  2.
2. 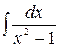 3.
3. 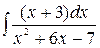
4. 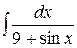 5.
5. 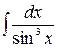
2. Find integrals using appropriate substitution:
1. 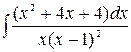 2.
2. 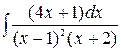 3.
3. 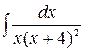 4.
4. 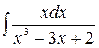
5. 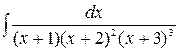
3. Calculate integrals:
1. 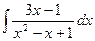 2.
2. 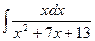 3.
3. 
4. 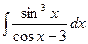 5.
5. 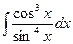 6.
6. 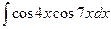
7. 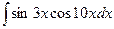 8.
8. 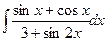
Homework:
Theoretical material: The definite integral. Problems leading to the definite integral. The Newton-Leibniz formula.
Solve problems:
Calculate integrals: 1. 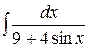 2.
2. 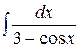
3. 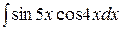 4.
4. 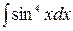 5.
5. 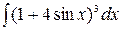 6.
6. 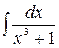
7. 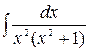 8.
8.  9.
9. 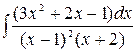
10. 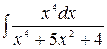
PRACTICAL CLASS ¹ 12-15
The definite integral. Problems leading to the definite integral. The Newton-Leibniz FORMULA. Applications to the computation of the integrals of plane figures areas. Calculation the arc length, the amount of body rotation. The improper integral
Theoretical questions:
1. Newton – Leibniz formula. 2. Basic methods of integration. 3. Geometric applications of the definite integral.
Classroom assignments:
1. Find integrals using Newton – Leibniz formula
1. 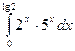 2.
2. 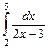 3.
3. 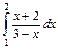 4.
4. 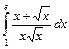
5. 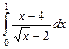
2. Calculate integrals: 1. 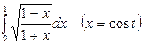 2.
2. 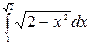 3.
3. 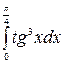 4.
4. 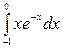 5.
5. 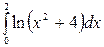
3. Find the area bounded by the curve 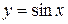 , the x-axis, and the lines
, the x-axis, and the lines  and
and 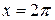 .
.
4. Find the area of the ellipse 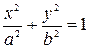 .
.
5. Find the area bounded by the curve  ,
, 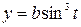 for
for 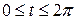 .
.
6. Find the area of the lemniscate  .
.
7. Find the length of the cissoid  from
from 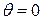 to
to 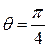 .
.
Homework:
Theoretical material: Functions of several variables and main properties. Partial derivatives and differentials.
Solve problems:
1. Find the area bounded by the parabola 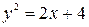 and the straight line
and the straight line  .
.
2 Find the area bounded by the ellipse  .
.
3. Find the area of the ellipse whose parametric equations are 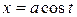 and
and  .
.
4. Find the parabola  from (0,0) to (-4,4).
from (0,0) to (-4,4).
Date: 2015-01-02; view: 1563
| <== previous page | | | next page ==> |
| The derivative of the function. Geometric and mechanical meaning. Table of derivatives. The differential of a function | | | Analytic geometry in the plane. |