MAIN METHODS OF INTEGRATION

Integration by substitution ( or change of variable )

Steps for Integrating by Substitution—Indefinite Integrals:

1. Choose a substitution u = g(x), such as the inner part of a composite function.

2. Compute .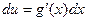

3. Re-write the integral in terms of u and du.

4. Find the resulting integral in terms of u.

5. Substitute g(x) back in for u, yielding a function in terms of x only.

6. Check by differentiating.

If f(x) is continous function, F(x)- its antiderivative and φ(х)- differentiable function, then

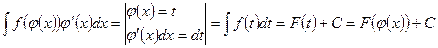
In the particular case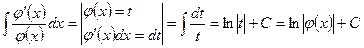

Example 8. To find 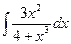. Notice that the numerator is the derivative of the denominator

Let 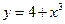. Differentiating gives 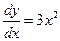and hence .

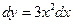Substituting this change of variable the integral becomes

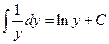
Now by expressing this result in terms of 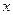we have shown that

.

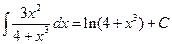Integration by parts

By the Product Rule for Derivatives, 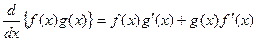. Thus,

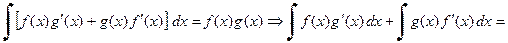
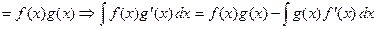. This formula for integration

by parts often makes it possible to reduce a complicated integral involving a product to

a simpler integral. By letting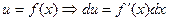

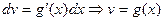
we get the more common formula for integration by parts: .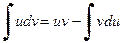

Example 9. Find .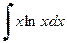

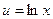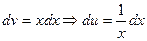Let and and 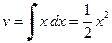. Thus,

.

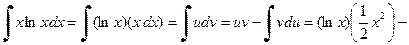
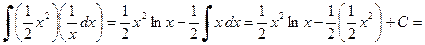
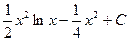It is possible that when you set up an integral using integration by parts, the resulting

integral will be more complicated than the original integral. In this case, change your

substitutions for u and dv.

Date: 2015-01-02; view: 1891