Relation and set functions.

The relation from the set A in the set B 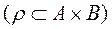is called the function from A into B, if

.

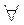
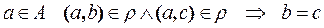The fact that f – function from the set A into the set B is registered as f: 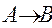or .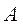

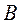Instead of the record 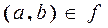we use . Such property of the relation is called as uniqueness or functionality.

If b=f(a) then a is called the argument, and b – the function value.

Let

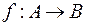, then 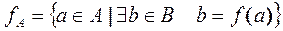is called the function of the definition range.

Let

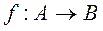, then 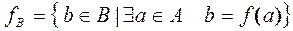is called the area of function values.

If 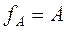, that function is called the total, and if 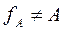– the partial.

The narrowing of the set function 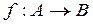into the set is called the function narrowing, 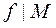,it is defined as follows:

.

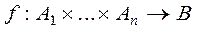is called the function of n arguments or n – local function.

Properties of function: Let 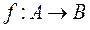. Then function 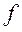is called the injective, if

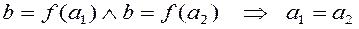, the subjective, if

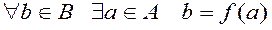, objective, if it injective and subjective

Properties of the relations

Let , i.e. 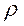– the binary relation on the set A

1) 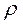– reflexive relation, if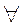

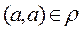
It is read as: for any element from the set А the steam (а, а) belongs to the relation 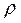that means that any element from the set А is in the relation with itself.

For example, we will consider the relation r={(a,b)}½a is a group mate of b,

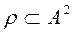, A – great number of students of technical school, then condi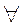tion means that any student of technical school is a groupmate of himself that obviously isn't correct, it means that the relation 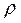isn't reflexive.

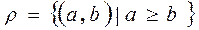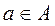
Let's consider the relation , , A – set of all real numbers, then condition 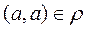means that any real number is more or equal to itself 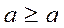, it is obviously correct, it means that the relation 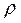is reflexive.

2) 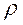– the symmetric relation, if .

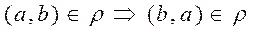It is read as follows: for any elements from the set А, if the pair belongs to the relation 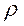and the pair 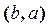belongs to the relation , that means that if an element a is in relation with b, then element b is in relation with a.

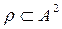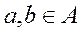
Let's consider the relation r={(a,b)}½a is a groupmate of b, , A – great number of students of technical school, then condition 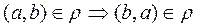means that if the student of technical school a is the groupmate of the student b, the student b studies in one group with a, it is obviously correct, the relation 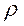is symmetric.

Let's consider the relation

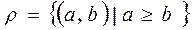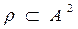, , A–set of all real numbers, then condition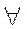 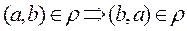means that if the condition 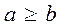is implemented, the condition 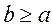is implemented too, that isn't correct, the relation 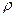isn't the symmetric.

3) – antisymmetric relation, if .

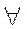
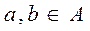
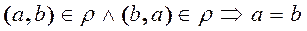It is read as follows: for any elements from the set A, if the pair belongs to the relation 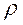and the pair belongs to the relation , then , that means that the relation 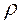can't contain the pair at the same time with the pair 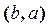, if the element a is distinct from an element b.

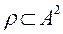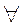
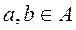
Let's consider the relation , , A – set of all real numbers, then condition 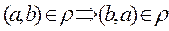means that if the conditions 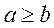and 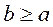are implemented, the condition 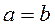is implemented too, it means that the relation is antisymmetric.

Let's consider the relation , , 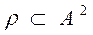A – set of all real numbers, then the condition means that if conditions and 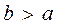are implemented, the condition 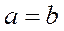is implemented too, that isn't correct, it means that the relation 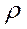isn't antisymmetric.

4) 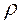– transitive relation, if

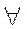
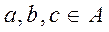
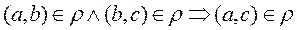. It is read as follows: for any elements from the set A, if the pair 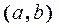belongs to the relation 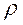, the pair 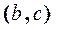belongs to the relation 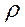and the pair 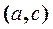belongs to the relation 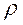, it means that if the element a is in the relation with b and the element b is in relation with c, then the element a is in relation with c.

Let's consider the relation r={(a,b)}½a is a groupmate of b, , A – great number of students of technical school, then condition 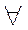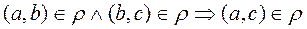means that if the student of technical school a studies in one group with b and student b studies in one group with с, then student а studies in one group with с, that is obviously correct, means, the relation 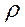is transitive.

5) 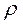– complete or linear relation, if

.

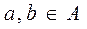
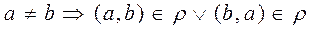It is read as follows: for any element from the set А, if 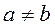, then the pair belongs to the relation 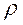, that means that for any two different elements a is in the relation with b or the element b is in relation with a .

Let's consider the relation

r={(a,b)}½a is a groupmate of b, ,

A – great number of students of technical school, then condition

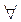
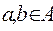
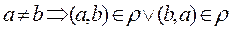means that for any two students of technical school a and b, or student a is the groupmate of the student b or student b is the groupmate of the student a, that obviously it is not true, it means that the relation 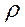isn't full.

Let's consider the relation , ,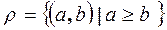

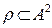A – set of all real numbers, then condition

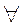
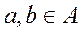
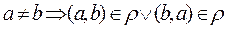means that for any two various numbers a and b or the condition 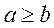is implemented or the condition 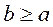is implemented, that, truly, means, the relation 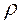is full.

Functions

The relation from the set A into the set B 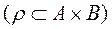is called the function from А into В, if

.

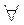
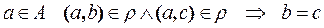The fact that f – function from the set A into the set B is registered as f: 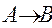or .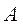

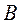Instead of record 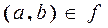let's use . Such property of the relation is called unambiguity or functionality.

If then 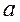is an argument and 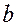is a value of function.

Let 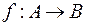, then 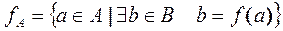is called the function range of definition.

Let 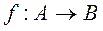, then 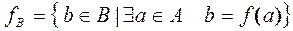is called the area of values of function.

If 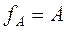, then the function is called as total and if 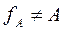– the function is partial.

Function narrowing 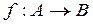on the set is called 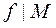,it is defined as follows: . 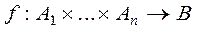is called the function of n arguments or n – local function.

Properties of the function

Let 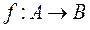. Then function f is called injective, if 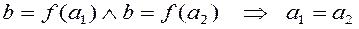, then the function F is subjective, if

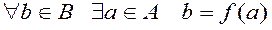, if it is injective and subjective.

Concept of the set

The concept of the set is one of the main concepts of mathematics. It has no exact definition and has, as a rule, it is explained with the help of examples.

Let's make the following intuitive definition of concept of the set:

Set – a certain set of objects. Objects of the set are called the set elements.

For example. The set of houses in one street, a set of natural numbers, a great number of students of group etc.

Sets are usually designated by capital Latin letters А, В, С, D, X, Y…, set elements are determined by small Latin letters – a, b, c, d, x, y…

To designate the fact that the object x is a set element of A, we use the following symbols: x 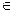А (it is read as: x belongs to 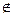А), x А designates that the object x isn't a set element of A (it is read as: x doesn't belong to А).

The set not containing any element is called an empty set (it is designated as Ø).

The sets with elements of which we make a concrete set is called the universal set (it is designated as U).

For example. U – great number of people on the earth, А – students of group E-102.

Sets can be represented by means of circles which are called Euler's circles, the universal set can be designated a rectangle.

Ways of presentation of sets

To establish the set, it is necessary to specify, what elements belong to it. It can be done in the various ways: 1) Enumeration of all elements of the set in braces.

Example: A= {Astana, Atbasar, Karaganda}

2) A characteristic predicate which describes the property of all elements entering into the set. The characteristic predicate is registered after the colon or the symbol « |».

For example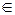. Р(x) = x N x < 8 – characteristic predicate.

M = {x: Р(x)} or M = {x: x N x < 8}. The set M can be represented the enumeration of its elements: M = {1, 2, 3, 4, 5, 6, 7}

For example. В = {x | x – natural number} = {2, 4, 6, 8, …}

If the set consists of a small amount of elements, it is convenient to represent it by enumeration of all elements, if there are a lot of elements or the set has infinite number of elements, it is established by means of the characteristic predicate.

The following numerical sets are known from the school course: N – set of natural numbers, N = {1, 2, 3, 4,…}; Z – set of integers, Z = {…, – 3, – 2, –1, 0, 1, 2, 3, 4,…}; Q – set of rational numbers,

Date: 2015-12-24; view: 1857