Duplication of the Cube

One of the "three famous problems of antiquity" was to find a geometrical construction for the edge of a cube having twice the volume of a given cube. It probably dates back to the time of the Pythagoreans. The Pythagorean theorem suggests a simple means for finding a square with twice the area of a given square - it is the "square" on the diagonal. If the side of the square is of unit length, we can thus solve the problem of finding a line segment of length 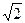. The corresponding problem of finding a segment of length was stated in a much more interesting form by the Greeks.

The Greek commentator of the period tells us of a letter supposedly written to Ptolemy I (not to be confused with the mathematician of the same name) concerning King Minos, who had a cubical tomb constructed for his son. The king was displeased with the size of the monument, however, and so ordered it doubled in size - by doubling the side. The commentator points out that this was an error as the tomb would thereby be increased fourfold in area and eightfold in volume; but he says, the geometers then tried to solve the problem.

A second and better known story is also told of the source of the problem. It is said that the gods sent a plague to the people of Athens. The people sent a delegation to the oracle at Delos to ask what could be done to appease the gods. They were told to double the size of the cubical altar to Apollo, and the plague would cease. They built a new altar, each edge of which was twice as long as each edge of the old altar. But since the gods' demand was not fulfilled, the plague continued. The story fails to relate what was finally done to appease the gods, but evidently the plague eventually left the city.

The search for solutions to this problem, to be carried out if possible with the restriction of using only straightedge and compass, was to lead the Greeks to many mathematical discoveries during the next several centuries. A compass-and-straightedge construction for this problem was not one of their discoveries, however, it can be proven that this cannot be done under these restrictions.

Menaechmus is given credit for discovering the conic sections in the process of trying to find a solution to this problem. He gave two solutions, one involving the intersection of two parabolas, and the other the intersection of a hyperbola and parabola. (It can easily be seen by analytic geometry, that when the equations y=x and xy=2 are solved simultaneously, then x= ). It should be emphasized that these were perfectly legitimate solutions, but they did not satisfy the Greek criterion of restricting the tools used, to straightedge and compass. Plato iscovered a mechanical solution, and during the third century B. C. Nicomedes used the curve called the conchoid. Diodes used the cissold to effect duplication.

Viete in 1593 proved that every cubic equation not otherwise solvable leads to either a duplication or a trisection problem. It remained for Descartes in 1637 to prove the impossibility of a solution by means of lines and circles. He showed that a parabola and a circle can be used to find the roots of a cubic equation, if the second-degree term is missing. Since every cubic may be reduced to one with no second-degree term, every cubic may be solved by means of a circle and a parabola. But the parabola may not be constructed with straightedge and compass, hence, neither the duplication of the cube nor the trisection of the angle may be so performed.

3.1.6. Greek Schools of Mathematics

Great minds of Greece such as Thales, Pythagoras, Euclid, Archimedes, Appolonius, Eudoxus, etc. (to produce) an amazing amount of first-class mathematics. The fame of these mathematicians (to spread) to all corners of the Mediterranean world and (to attract) numerous pupils. Masters and pupils (to gather) in schools which though they had few buildings and no campus (to be) truly centres of learning. The teaching of these schools (to dominate) the entire life of the Greeks.

Despite the unquestioned influence of Egypt and Babylonia on Greek mathematicians, the mathematics produced by the Greeks (to differ) fundamentally from that which (to precede) it. It (to be) the Greeks who (to found) mathematics as a scientific discipline. The Pythagorean school (to be) the most influential in determining both the nature and content of Greek mathematics. Its leader Pythagoras (to found) a community which (to embrace) both mystical and rational doctrines.

The original Pythagorean brotherhood (to be) a secret aristocratic society whose members (to prefer) to operate from behind the scenes and, from there, to rule social and intellectual affairs with an iron hand. Their noble born initiates (to be taught) entirely by word of mouth. Written documentation (not to be permitted), since anything written (may) give away the secrets largely responsible for their power. Among these early Pythagoreans (to be) men who (to know) more about mathematics then available than most other people of their time. They (to recognize) that vastly superior in design and manageability Babylonian base-ten positional numeration system (may) make computational skills available to people in all walks of life and rapidly democratize mathematics and diminish their power over the masses. They (to use) their own non-possitional numeration system (= standard Greek alphabet supplemented by special symbols). Although there (to be) no difficulty in determining when the symbols (to represent) a number instead of a word, for computation the people of the lower classes had to consult an exclusive group of experts or to use complicated tables- and both of these sources of help (to be controlled) by the brotherhood. The Pythagoreans (can) tell the tradesmen how such tables and devices (e. g., Abaci) were to be used but never how to make them or what the hidden patterns (to be) which (to make) them possible.

For Pythagoras and his followers the fundamental studies (to be) geometry, arithmetic, music, and astronomy. The basic element of all these studies (to be) number not in its practical computational aspects, but as the very essence of their being; they (to mean) that the nature of numbers should (to be conceived) with the mind only.

In spite of the mystical nature of much of the Pythagorean study the members of community (to contribute) during the two hundred or so years following the founding of their organization, a good deal of sound mathematics. Thus, in geometry they (to develop) the properties of parallel lines and (to use) them to prove that "the sum of the angles of any triangle is equal to two right angles". They (to contribute) in a noteworthy manner to Greek geometrical algebra, and they (to develop) a fairly complete theory of proportion though it (to be limited) to commensurable magnitudes, and (to use) it to deduce properties of similar figures. They (to be aware) of the existence of at least three of the regular polyhedral solids, and they (to discover) the incommensurability of a side and a diagonal of a square.

The "Pythagorean" theorem (to be) one of the most important proposions in the entire realm of geometry. There (to be) no doubt, however, that the "Pythagorean property": c²=x²+y² (to be known) prior to the time of Pythagoras; there (to exist) clay tablet texts which (to contain) columns of figures related to Pythagorean triples. The frequent textbook reference to Egyptian "rope-stretchers" and their knotted surveying ropes as proof that these ancients (to know) the theorem (to be) erroneous. While it (to be known) that the Egyptians (to realize) as early as 2000 В. С. that 4²+3²=5², there (to be) no evidence that the Egyptians (to know) or (to be able) to prove the right angle property of the figure involved. Pythagoras (to be credited) with the proof of this property which (to be) true for all right trianges, and for all natural numbers. Although much of this information (to be known) already to the ancients of earlier times, the deductive aspect of geometry (to be exploited and advanced) considerably In the work of the Pythagoreans.

The mysticism of this celebrated school (to arouse) the suspicion and dislike of the people who finally (to drive) the Pythagoreans out of Cro-tona, a Greek seaport in Southern Italy and (to burn) their buildings. Pythagoras (to be murdered) but his followers (to scatter) to other Greek centres and (to continue) his teachings. The Pythagoreans (to be credited) with giving the subject of mathematics special and Independent status. They (to be) the first group to treat mathematical concepts as abstractions and they (to distinguish) mathematical theory from practices or calculations. They (to prove) the fundamental theorems of plane and solid geometry and of "arithmetica" - the theory of numbers.

More widely known than the Pythagoreans (to be) the Academy of Plato which (to have) Aristotle as its most distinguished student. The latter then (to found) his own school at the time of Plato's death. Plato's pupils (to be) the most famous philosophers, mathematicians and astronomers of their age. Under Plato's influence they (to emphasize) pure mathematics to the extent of ignoring all practical applications and they (to add) immensely to the range of mathematics.

3.1.7. The History of Geometry

The story of the history of geometry, like that of many other growing and changing subjects, is composed of two intertwined strands. One strand narrates the growing content of the subject and the other the changing nature of the subject. The following is a brief outline of the birth and the development of Geometry.

Date: 2015-12-18; view: 1916