PART B – ANSWER TWO OUT OF THREE QUESTIONS IN THIS PART

TERM 1 TEST

Physics

Instructions to Candidates

1. Answer ALL questions in Part A and TWO questions in Part B
2. No dictionaries are permitted
3. Only the following calculators are permitted: Casio FX83MS, FX83ES, FX83WA (battery powered) and Casio FX85MS, FX85ES, FX85WA (solar powered).
4. 10 minutes reading time is allowed in addition to the 2 hours for completing the paper
5. You may NOT start writing during the 10 minute reading time at the beginning of the test

Date: Monday 12^th December 2011 Location: Cruciform LT2

Time:9.30am – 11.30am Length: 2 Hours

The total mark for the exam is 120 marks. Part A has 96 marks and Part B has 24 marks. Part A comprises 80% of the total mark and Part B comprises 20% of the mark.

Universal gravitational constant G = 6.67 × 10^-11 N m² kg^-2

Gravity field at the Earth’s surface g = 9.81 m s^-2

Distance Earth-Moon d_EM = 3.84 × 10 ⁸ m

PART A – ANSWER ALL QUESTIONS IN THIS PART

Question 1

One can show that the average speed, v, of molecules in a fluid can be expressed as:

,

where μ is the viscosity of the fluid, d is a characteristic distance, and ρ is the density of the fluid. Use dimensional analysis to find the dimension of the viscosity, μ. (6 marks)

Question 2

The moment of inertia of a uniform rod of mass M and length L about an axis perpendicular to it and passing through its centre of mass is given by:

A student records the following experimental measurements on her lab book:

I = (0.188 ± 0.025) kg m²

L = (96.0 ± 1.2) cm

(a) Calculate the mass M of the rod (to 3 significant figures). Give your answer in SI units.

(b) Calculate the fractional uncertainty on M (to 3 significant figures).

(c) Calculate the absolute uncertainty on M (to 2 decimal places).(10 marks)

Question 3

A student throws a ball from a window at a height H = 3.00 m above the ground. When the ball leaves the student’s hand at t = 0, it is moving at a speed v₀ = 10.0 ms^-1 and its velocity vector makes an angle θ = 20° below the horizontal. Air resistance is neglected.

(a) Calculate the time t when

the ball hits the ground.

(b) At what horizontal distance, d,

will the ball hit the ground?

(12 marks)

Question 4

The Moon, assumed to be in uniform circular motion around the centre of the Earth, has a period of rotation, T, of 27.3 days. Using the appropriate data given at the beginning of this paper, calculate:

(a) the speed of the Moon along its orbit

(b) the magnitude of the acceleration vector of the Moon orbiting the Earth.

The force F between two masses, m₁ and m₂, a distance r apart can be found using the equation, where G is the universal constant of gravitation:

,

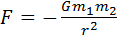(c) calculate the mass of the Earth. (10 marks)

Question 5

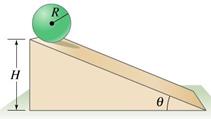Consider a uniform solid sphere of mass M and radius R rolling, without sliding, down an inclined plane making an angle θ with the horizontal, as shown. The moment of inertia of the solid sphere is: .

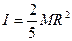(a) Derive an expression for the speed, v, of the sphere’s centre of mass at the bottom of the plane as a function of the height of the incline, H and the acceleration due to gravity, g.

(b) We now consider a hollow sphere (or spherical shell) of same mass M and same radius R. Will the speed of the empty sphere’s centre of mass be larger or smaller than in part (a)? Explain why. (10 marks)

Question 6

Two cruiser ships have positions vectors (of magnitudes measured in km), withrespect tothe capital city of an island, given by:

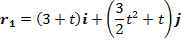
respectively, where t (measured in hours) is the time until they reach the island’s port. Give your answers to 3 significant figures.

(a) Find their separation in km, 3 hours before they reach the island.

(b) Find the speed of each ship.

(c) Determine their relative speed 3 hours before they reached the island.

(d) The two ships met in the sea, t hours before they arrived in the island. Calculate t.

(10 marks)

Question 7

A spring of constant k is extended by a length Dx with the help of an external force F_ext.

(a) Write down Hooke’s law for the restoring force F_rest.

(b) Use Hooke’s law and the definition of work done by a force (otherwise with the help of a diagram) to show that the energy stored in the spring when extended by Dx = l with an external force F_ext is: E = ½ k l². (8 marks)

Question 8

(a) Explain either with words or with equations the conditions that must be fulfilled for an object to be in static equilibrium.

A man leans against a vertical ice wall (see figure). His feet are at a distance a = 0.914 m from the wall and his extended length is L = 2.10 m. . His centre of mass (com) is a distance d = 0.948 m from where his feet are in contact with the ground.

(b) Draw a free body diagram for the man.

(c) Given that the man is about to start to slide, calculate the coefficient of static friction between his feet and the ground.

(10 marks)

Question 9

The displacement y of a particle in a travelling wave is given by:

,

where x and y are in metres and t is in seconds.

(a) Determine the wave’s frequency, wavelength and speed.

(b) Consider a particle at x = 0.14 m. What is its speed at time t = 0.7 s?

(10 marks)

Question 10

(a) Give the definition of a transverse and longitudinal wave and one example of each.

Monochromatic light from a laser is incident on two slits in a Young’s slit experiment. The slits 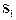and are a distance, d, apart and they are perpendicular to the plane of the diagram. An interference pattern is formed on the screen (see figure).

		screen

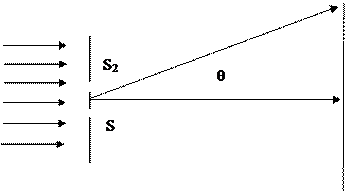
(b) Show, using a clearly labelled diagram, that interference maxima occur along directions given by:

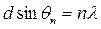where n is an integer.

(c) If the light’s wavelength used is 589 × 10^-9 m, the angular separation, θ, between the central maximum and the next maximum is 3.50 × 10^-3 rad. For what wavelength would the angular separation be 10% greater?

(10 marks)

PART B – ANSWER TWO OUT OF THREE QUESTIONS IN THIS PART

Question 1

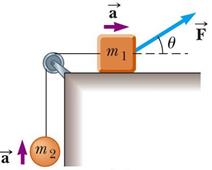A block of mass m₁ = 0.500 kg on a rough horizontal surface is connected to a mass m₂ = 1.00 kg by a string of negligible mass over a lightweight, frictionless pulley as shown below. A force of magnitude F = 20.0 N at an angle θ =30° above the horizontal is applied to the block of mass m₁ and the block slides to the right. The coefficient of kinetic friction between the block and the surface, μ_k , equals 0.200.

(a) Draw a clear free body diagram of each mass.

(b) By applying Newton’s second law to each mass and clearly showing your working, show that the acceleration of the two objects, a, can be expressed as:

(c) Calculate the acceleration a. Given that the mass m₁ starts to move at t = 0 s, calculate the time for the mass m₁ to moved 80.0 cm to the right.

Marks) Question 2

The sequence of Figures (i), (ii) and (iii) below, shows the collision of two masses M = 3.00 kg and m = 1.00 kg that are attached at the ends of two light inextensible strings of length
l = 8.00 cm. Mass m is initially at height h = 4.00 cm, in Figure (i) and after the collision both masses stick together, in Figure (ii) and they reach a height y cm, in Figure (iii).

Figure (i)Figure (ii)

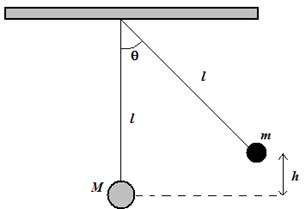
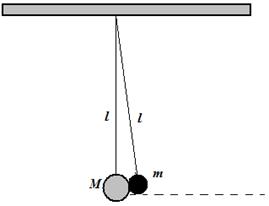
Figure (iii)

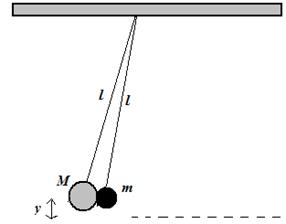
By assuming that the masses are point particles, find:

(a) the common speed of the masses, in Figure (ii)

(b) the height y cm reached by both masses, in Figure (iii)

(c) the energy lost in the collision, and name three possible forms of this energy loss.

(d) The energy calculated in part (c) is lost very rapidly during the collision, typically 1/100 of the period T of free oscillations of the system after the collision. By assuming that the system after the collision executes simple harmonic motion, calculate the average power lost during the collision. (12 marks)
Question 3

A spring of constant k = 12.0 Nm^-1 is attached to a mass m = 0.400 kg and set horizontally on a frictionless surface. The mass is pulled from the equilibrium position so that the spring is stretched 0.100 m in the positive x-direction, and is then released at t = 0 s.

(a) What is the amplitude A of oscillations?

(b) At what time t does the mass first pass through the point of coordinate ?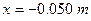

(c) Calculate the magnitude of the velocity at this time.

(d) Calculate the fraction of the total energy that is stored as elastic potential energy in the spring at this time.

(e) Sketch a graph of the position of the mass, x, as a function of time for 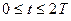, where T is the period of oscillations.

(f) Explain in words how the motion sketched in (e) would change if the system is lightly damped.

(12 marks)

Date: 2015-12-18; view: 684