Decimal to Unsigned Binary Conversion

Converting from decimal to unsigned binary is a little more complicated, but it still isn't too difficult. Once again, there is a well-defined process. To begin with, it is helpful to remember the powers of 2 that correspond to each bit position in the binary numbering system. These were presented in Figure 4 for the powers of 2⁰ up to 2⁷. What we need to do is separate the decimal value into its power of 2 components. The easiest way to begin is to find the largest power of 2

that is less than or equal to our decimal value. For example if we were converting 75₁₀ to binary, the largest power of 2 less than or equal to 75₁₀ is 2⁶ = 64.

The next step is to place a 1 in the location corresponding to that power of 2 to indicate that this power of 2 is a component of our original decimal value. Next, subtract this first power of 2 from the original decimal value. In our example, that would give us 75₁₀ – 64₁₀ = 11₁₀. If the result is not equal to zero, go back to the first step where we found the largest power of 2 less than or equal to the new decimal value. In the case of our example, we would be looking for the largest power of 2 less than or equal to 11₁₀ which would be 2³ = 8. When the result of the subtraction reaches zero, and it eventually will, then the conversion is complete. Simply place 0's in the bit positions that do not contain 1's. Figure 6 illustrates this process using a flowchart.

If you get all of the way to bit position zero and still have a non-zero result, then one of two things has happened. Either there was an error in one of your subtractions or you did not start off with a large enough number of bits. Remember that a fixed number of bits, n, can only represent an integer value up to 2ⁿ – 1. For example, if you are trying to convert 312₁₀ to unsigned binary, eight bits will not be enough because the highest value eight bits can represent is 2⁸ – 1 = 255₁₀. Nine bits, however, will work because its maximum unsigned value is 2⁹ – 1 = 511₁₀.

Figure 1.6Decimal to Unsigned Binary Conversion Flow Chart

Example1Convert the decimal value 133₁₀ to an 8 bit unsigned binary number.

Solution Since 133₁₀ is less than 2⁸ – 1 = 255, 8 bits will be sufficient for this conversion. Using Figure 4, we see that the largest power of 2 less than or equal to 133₁₀ is 2⁷ = 128. Therefore, we place a 1 in bit position 7 and subtract 128 from 133.

Bit position

133 – 128 = 5

Our new decimal value is 5. Since this is a non-zero value, our next step is to find the largest power of 2 less than or equal to 5. That would be 2² = 4. So we place a 1 in the bit position 2 and subtract 4 from 5.

Bit position

5 – 4 = 1

Our new decimal value is 1, so find the largest power of 2 less than or equal to 1. That would be 2⁰ = 1. So we place a 1 in the bit position 0 and subtract 1 from 1.

Bit position

1 – 1 = 0

Since the result of our last subtraction is 0, the conversion is complete. Place zeros in the empty bit positions.

Bit position

And the result is:

133₁₀ = 10000101₂

Example 2 Convert the decimal number 99 to its binary equivalent:

Divide 99 by 2. The quotient is 49 with a remainder of 1; indicate the 1 on the right.

Divide 49 by 2(the quotient from the previous division). The quotient is 24 with a remainder of 1, indicated on the right.

Divide 24 by 2. The quotient is 12 with a remainder of 0, as indicated .

Divide 12 by 2. The quotient is 6 with a remainder of 0, as indicated.

Divide 6 by 2. The quotient is 3 with a remainder of 0, as indicated.

Divide 3 by 2. The quotient is 1 with a remainder of 1, as indicated.

Divide 1 by 2. The quotient is 0 with a remainder of 1, as indicated. Since the quotient is 0, stop here.

The base 2 number is the numeric remainder reading from the last division to the first

Binary Addition

Consider the following binary addition problems and note where it is necessary to carry the 1:

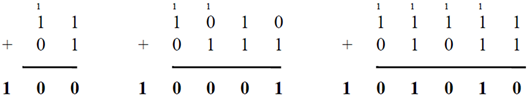
Date: 2015-12-17; view: 1011