DIFFUSER PROPORTIONS

Arriving at the proper size for a diffuser is, thanks to the work of several researchers, almost entirely a cut-and-dried proposition. Diffusers should have an 8-degree included taper for maximum energy recovery, and an outlet area 6.25-times that of their inlet. Thus, a diffuser to be attached to an inlet having a 1.5-inch diameter should have an outlet of 3.75-inch diameter. Outlet diameters for diffusers of all inlet diameters may be determined in the following manner:

Where D₂ is the diffuser outlet diameter

D_l is the diffuser inlet diameter

6.25 is the outlet/inlet ratio constant

Although these diffuser diameters, tied to the 6.25 constant, remain the same, diffuser length may be varied, as there are reasons for using diffuser tapers other than 8-degrees. That taper does the best overall job of energy recovery, but it is possible to get a stronger inverted wave with diffuser tapers greater than &degrees, at the expense of wave duration. Conversely, one also may extend the wave duration by accepting some diminishing of its amplitude with shallower tapers. A long wave duration spreads an engine's power band; a short-duration wave with high amplitude is best for maximum power at peak revs. Diffusers having tapers of more than 10-degrees return a wave of such brief duration as to be almost useless even for a road racing engine coupled to the rear wheel via a multi-speed, ultra-close ratio transmission, and also are rather inefficient in terms of energy recovery. For that reason, I do not recommend that you use a diffuser taper greater than 9-degrees even when planning an expansion chamber for a road racing machine, as you may otherwise find it impossible to keep the engine operating within its power band. At the opposite extreme, do not try to use anything below a 5-degree taper diffuser in an expansion chamber for an off-road motorcycle. You will find that even a 5-degree taper results in a diffuser that is almost impossible to accommodate within the system's tuned length, and that it returns an inverted wave to the exhaust port too feeble in amplitude to be very effective in scavenging a two-stroke engine. As a rule of thumb, I would suggest employing diffusers having tapers of 8- to 9-degrees for road racing, small displacement motocross bikes (up to 250cc) should have tapers of 7- to 8-degrees, and for big motocross bikes, tapers of 6- to 7-degrees. These last usually have more horsepower than they can comfortably apply to the ground anyway, and one does not therefore give away anything by extending their power range at the expense of peak horsepower.

All of the tapers given are for single-taper diffusers. In the future we shall be seeing more of multi-taper diffusers, which I first saw on the Yamaha GP racing machines and which have since begun to appear on most of Japan's expansion chamber-equipped production motorcycles. These multi-taper diffusers would seen) to be intended to accommodate themselves to the fact that a wave, passing clown a diffuser - or any containing vessel with diverging walls -tend to separate from those walls at the diffuser entry unless the taper is slight, but is willing to accept substantially greater angles of divergence once it has moved into the diffuser far enough to have expanded and slowed. From this behavior, if I understand it correctly, one must conclude that the best diffuser would be one diverging along exponential lines -like a trumpet. Of course, such a shape would be excruciatingly difficult to fabricate, and I think it is for that reason Yamaha and Suzuki chose to employ instead diffusers with two or three tapers. My own investigation into this matter is still in its very early stages, and I cannot offer any opinion (much less 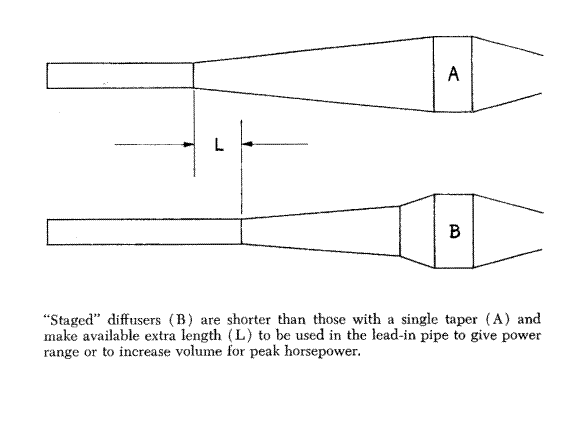facts) except to note that Yamaha has been working with diffusers tapered 7-degrees for 70-percent of their length, and the remaining 30-percent tapered 12-degrees. Both Yamaha and Suzuki have recently begun to connect these two-stage diffusers to the exhaust port with a lead-in pipe that is also tapered 2- to 3-degrees. This slight taper probably is provided to minimize flow resistance and thereby enhance the lead-in pipe's ability to inertia-evacuate the cylinder, rather than to function as part of the diffuser.

Incidentally, the use of two-stage diffusers also facilitates coping with the often-conflicting requirements of expansion chamber volume and lead-in pipe length. A diffuser proportioned 7^o / 12^o, 70% / 30%, is somewhat shorter than a diffuser having a straight 8-degree taper when both are constructed to the same 6.25:l outlet/inlet area rule. This reduction in diffuser length may be added at the lead-in pipe, or at the chamber's parallel-wall section, where the diffuser and baffle cone are joined. In either case, with a longer lead-in pipe or added chamber volume, the overall effect is to increase power output below the power peak - with volume having its most pronounced effect high on the engine speed scale, near the power peak; length added to the lead-in pipe brings about a somewhat more serious drop in maximum power, but also lends a marked increase in low speed torque. These effects, it should be noted, tend to modify the choice of diffuser tapers, as a short, steep-taper diffuser provides room for a longer lead-in pipe or added chamber volume - both of these tending to offset the power range-narrowing influence of such diffusers.

Some departures from the 6.25:l area ratio rule may also be desirable on occasion: when a lead-in pipe diameter is exaggerated, relative to exhaust port area and cylinder size, in the interest of low-range performance, you may find that following the ratio rule results in an expansion chamber of such monstrous diameter that it simply cannot be fitted on the motorcycle for which it is intended, and in that case an appropriate downward adjustment in diameter is indicated.

Should this consideration of inconvenient bulk lead you to depart from the dimensions required by my formulae, think twice before you succumb to the temptation to flatten the expansion chamber. In the first place, you'll upset all the area progressions through the diffuser; an 8-degree diffuser, flattened ever so slightly, is no longer an 8-degree diffuser. Moreover, even if you calculate the areas so that you have a rounded wedge with the correct inlet/outlet area proportions, wave energy recovery will still suffer. Those waves simply do not like being puffed through anything but a cone; even less do they like a cone that has been dented or notched to clear a frame tube or to provide ground clearance. They can "feel" every change in cross-section in the containing vessel. They are, however, willing to follow even the most abrupt jog in the system: you can resection the diffuser cone and kink it all over the place to make the 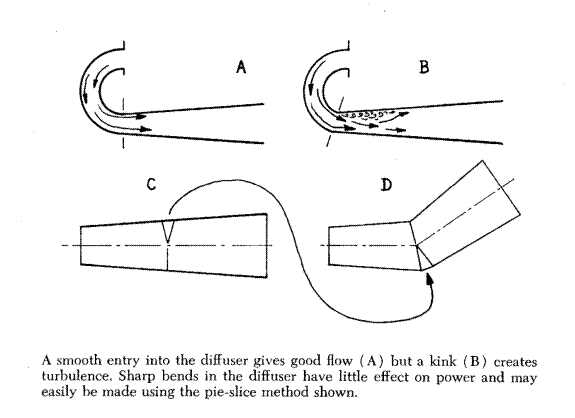expansion chamber fit the motorcycle, and the wave will never know the difference. Sonic waves may be able to feel even the most minute changes in section; they will make any turn you can build into the system without slowing or losing any of their energy.

The only part of the system where you must be careful to provide smooth turns is up at the lead-in pipe and at the entry to the diffuser. Through that section, gas velocity is very high, and while the wavewon't care about sharp jogs, such jogs will have a bad effect on gas flow - which is a different matter entirely ( gas flow involves the movement of matter; a wave is just energy, and being without mass, is also without inertia and therefore cares nothing about sharp corners. At least, that is very substantially the case here, where the velocities, etc. involved are low enough to fall within the scope of Newtonian physics; Einstein's unified field work is hardly applicable at wave speeds of such limited magnitude).

If efficiency were the only consideration in current expansion chamber design, it would be possible to depart fairly substantially from the round cross-section back at the chamber's middle portion. Actually flattening the chamber is still not a good idea, but it can be squared off somewhat without greatly compromising its basic power-enhancing properties. Two years ago, I would have recommended precisely that sort of modification in instances where installation was a problem. Now, with the drive against noise well and truly underway, any departure from round is to be considered poor design practice. Why? Because those waves I have been talking about are very strong, and will make even a round-section chamber's walls ring like a bell (to be specific, a cow-bell) just like the engine is shooting marbles out its exhaust port. These pulses, which are strong enough to set up a ringing even in the relatively stiff walls of a round-section chamber, will make any flat areas in the expansion chamber's walls pant in and out like a drum-head. This vibration is of course transmitted into the surrounding atmosphere as a hellishly loud noise, and no matter how effective a muffler you may add back at the chamber's outlet pipe, the motorcycle's overall noise output will nonetheless be very high. The noise source just described can only .be minimized by either making the chamber out of very heavy steel, or by giving it a shape that resists pulsing; the round-section chamber may ring somewhat, but it cannot actually pulse in and out even when made of very light-gauge material. This pulsing of the chamber's walls has another highly undesirable side effect: it makes the permanent attachment of a bracket or heat shield very difficult. Most fasteners will fairly quickly fracture from the severe vibration, leaving the heat-shield to drop away - which is bad, but not as bad as when the same vibration fractures a major mounting bracket and the entire expansion chamber conies adrift. For all these reasons, the round-section expansion chamber, although inconveniently bulky at times, really seems to be the best choice.

BAFFLE CONES

We have already noted that the baffled end of most expansion chambers is conical. This cone lends the chamber rather more pleasing lines than it would have with a flat end, but that is not its reason for being. The reason is that if we end the chamber very abruptly, with a flat plate, the wave reflections away from it will also be very abrupt: strong, but of a duration too brief to provide the desired port-plugging effect except within extremely narrow limits in engine speed. A conical baffle, on the other hand, extends the wave reflection time (as reflection occurs down its entire length) and, because its effects are thus felt over a wider engine speed range, the engine's useful power band is broadened. Obviously, here, a long, gently tapered baffle-cone will extend an engine's power range more than a shorter, more sharply tapered cone in the customary trade-off between range and peak power. These tapers should be, in most cases, twice that of the diffuser used in the expansion chamber. Thus, in a chamber having an 8-degree diffuser, the baffle-cone should be tapered 16-degrees. That is the rule in general. However, wide variations are possible and may be employed to cope with a specific situation. The largest taper angle you should use is 20-degrees; the smallest, 14-degrees. And you may, to obtain a particular effect, “mismatch” diffusers and baffle cones in any combination. 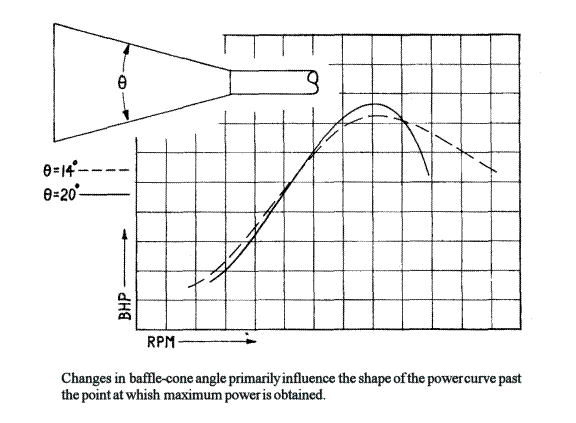The thing to remember is that there is a peculiar side to the power-range broadening effect of the baffle-cone: most of it is on the part of the engine's power curve past the horsepower peak. Thus, for an engine that has proven to be rather fragile when pressed beyond its rpm red-line, you may terminate the expansion chamber with a 20-degree baffle cone, and rest assured that if the system's tuned length is established to place the horsepower peak, say, 500 rpm below the danger mark, the engine will resist very strongly any effort to get it spinning faster.

My experience in dynamometer-testing various expansion chamber configurations has shown that a 20-degree baffle-cone gives a good, strong power peak - and then simply cuts the engine dead, in terms of output, if you try to force the revs any higher. A 15-degree baffle-cone, in contrast, gives a somewhat lower maximum output - but helps the engine maintain its output well after the peaking speed has been exceeded. The implications of this influence on an engine's power curve should be obvious: motocross bikes can gain in engine flexibility from a long, gently tapered baffle-cone, but if you are “tuning” for some young man who often forgets to protect the engine from over-exerting itself by changing gears, then you can use a 20-degree baffle cone. It will remind him about the gear lever by chopping the power drastically every time he tries to use too many revs.

There is another thing you need to know about those baffle-cones before you can design your own expansion chambers: they do, as stated earlier, reflect over their full 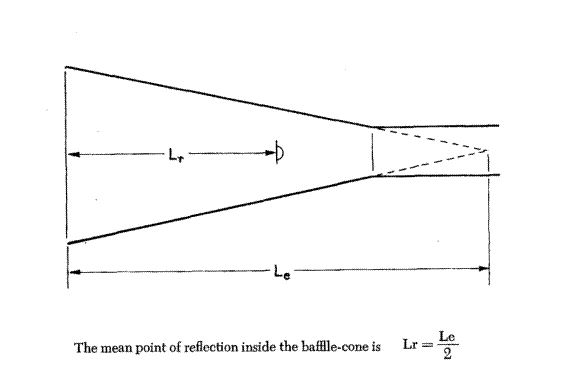length any wave entering them, but there is not an even reflection, for reasons too numerous and involved for serious discussion here. What you do find, however, is that there is a “mean” point of reflection which is, as I said earlier, slightly more than half-way down the baffle-cone's length. The “tuned length” we discussed before, the length so critical to the expansion chamber's performance, is actually the distance from the exhaust port window, at the piston face, measured along the exhaust system's center-line out to this point of mean reflection. This midway point seems to be at the halfway point of the complete cone, which would be half the length of the cone if the cone were complete, right out to a sharp tip, instead of being truncated at its small end to make room for the outlet pipe. You can find this point of mean reflection either by drawing the complete cone, measuring, and dividing its length in half, or by using this simple formula:

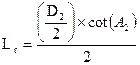
Where L_r is the distance from the baffle-cone's inlet to the mean point of reflection

D, is the baffle-cone's inlet diameter

A, is half the baffle-cone's angle of convergence (i.e. for a 16-degree cone use 8-degrees, etc.)

While we are on this particular subject, I will also give you the formula for finding the length of a cone, given its taper, major and minor diameters. The formula is as follows :

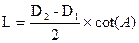
Where L is length

D₂ is the cone's major diameter

D₁, is the cone's minor diameter

A is half the angle of divergence, or convergence.

OUTLET PIPES

Having gotten past the business of diffusers and baffle-cones, we can proceed onward to the lengths and diameters of lead-in and outlet pipes. The latter will, if the rest of the expansion chamber is proportioned fairly closely in accord with the advice I have given, have a diameter between .58- and .62-times that of the lead-in pipe, and a length equal to 12 of its own diameters. It is simply a pressure-bleed resister, which prevents the free escape of exhaust gases from inside the expansion chamber and thereby creates a backpressure to enhance the port-plugging efforts of the wave reflected by the baffle-cone.

This outlet pipe is much more sensitive to diameter than length. The rule I have provided for diameter will get you very close to the optimum, if the rest of the chamber is proportioned correctly (or at least as I have indicated, which I hope will amount to the same thing) and the length, of 12-diameters, will also be very close. Even so, they will only be “close” and I have found few instances, in my own experimenting, when a session of cut-and-try on the dynamometer did not lead me to a slightly different diameter and length for best results. You probably do not have a dynamometer, and that bit of news is in all likelihood not something you wanted to hear. Nonetheless, it is true. You will not get optimum results here simply by following the instructions I provide. In fact, a tad of adjusting is required, to meet a particular set of requirements, to make any strictly-formula expansion chamber give maximum performance. But there is a very particular problem associated with the outlet pipe that you should know about: Simply stated, the problem is that if you make the outlet pipe too small in diameter, or give it too much length, (both tending to over-restrict the chamber's outlet passage in terms of flow capacity) then there will be a price to be paid in overheating. I frankly do not know the mechanism involved in this; I only know that if the outlet is too restricted, engine temperature is very greatly elevated - and Yamaha's Naito has said that the same unfortunate result will be observed if the expansion chamber's baffle-cone is tapered too abruptly. From what I have seen, this increase in temperature is especially sharp at the piston crown, which tends to be the power-limiting part in a two-stroke engine in any case. So, you should keep a sharp eye on your engine's piston. There will be temperatures high enough to darken the underside of the piston crown, due to baked-on oil forming there, when the engine is healthy; just don't ignore the warning sign you see when that oil begins to char. The next thing you see, after you see ash, will be a hole.

Actually, the worst side of this whole matter of selecting the right outlet pipe is that while power rises quite sharply as you work your way down from a too-large outlet pipe diameter, there will be only a slight decrease in power output when you have gone too far in restricting the outlet. Therefore, unless you have a dynamometer and instrumentation for measuring engine temperatures, make all errors on the large side of the diameter you get by multiplying lead-in pipe diameter by the 0.58-0.62 factor I have provided. In other words, if the factor-derived diameter (taken from a lead-in pipe diameter of say, 1.75-inches) is from 1.015 to 1.085-inches, then you should not try to use a piece of one-inch tubing for that outlet pipe, as its nominal diameter is an outside measurement. Subtract for a wall thickness of, say, 0.049-inch, and you'll have a passage only 0.902-inch in diameter. That isn't large enough to be safe - nor would a tube having a nominal diameter of l ¹/₈-inches, with an inside diameter of 1.027-inches be entirely safe. When skirting that close, go up to the next largest available diameter - in this case it would be l ¹/₄-inches –and run the engine long enough and hard enough to permit a valid “reading” of the piston crown's underside. If it shows no sign of excessive heat, you can try a slightly smaller outlet pipe, and then check the piston again.

LEAD-IN PIPES

There probably is a better, closer, rule for determining outlet pipe diameter -if only because the rule I have offered is tied to the diameter of the expansion chamber's lead-in pipe, which is very, verydifficult to determine on a strictly theoretical basis. For engines having exhaust port timings and port widths typical in racing terms, the expansion chamber's lead-in pipe should have a diameter providing an area 10- to 15-percent greater than that of the port window. But that only applies, I have found, when the parameters are as stated, and only then when a power curve very distinctly biased toward maximum output at maximum revs is desired. For motocross applications, the diameter chosen will be one that can be used in combination with a considerable pipe length to broaden the power range. In some instances, lead-in pipes are used with cross-sectional areas representing 150-percent of the exhaust window area. As a general rule, you may assume that the manufacturer of your particular engine knows more about lead-in pipe areas than you, or I, and you can't get into trouble following his lead. You may, by ignoring the possibilities in other directions, miss an optimum by some smallish percentage - but you won't get into trouble.

The thought may have occurred that my instructions are, in this regard, something far short of precise. And so they are, for good reason: the choice of lead-in pipe diameter must be shaped not only by unit cylinder displacement, port timing/area, and according to the application you have in mind for the engine-but also with an eye toward the lead-in length, and the configuration of the diffuser to which the pipe attaches. All of these things have their effect, but I have not as yet been able to isolate each item well enough to arrive at a quantitative pattern. So, for the moment, I make do with a qualitative understanding and a couple of handy rules-of-thumb: the first you already know (regarding the rough relationship between the port and pipe cross-section area); the second rule (more a suggestion, really) is that for maximum horsepower only, you should give the lead-in pipe a length equal to from 6 to 8 of its diameters, while for a broader power curve (and at some expense to the maximum) you may want to use up to 11-times pipe diameter. All these lengthy are, of course, not just that of the pipes themselves, but also include the distance from the pipe mounting flange through the port to the piston face. Afinal note on lead-in pipe length: if, for reasons of easier installation, or a broadening of the power range, or both, you decide upon a lead-in pipe length greater than 8-times its diameter, plan to increase its diameter slightly. Resistance to flow is increased with length, and this can and should be offset by giving the gases a larger passage. Ideally, this reduction in resistance would be accomplished by using a lead-in pipe having a slightly-diverging taper (2 or 3degrees) but that may represent a more difficult fabrication job than you care to undertake.

After you have finished the job of designing an expansion chamber exhaust system, the thing will have to be translated from a set of dimensions into metal, or you'll never know whether or not the design is any good. You can, of course, build the whole thing yourself, but I would not recommend that approach. Especially, I would caution against attempting to roll your own cones, as this is the kind of job that takes endless hours when you don't have the proper tools and is likely to turn out badly anyway. Go to a sheet-metal shop and pay them to make your cones; they'll get it done in much less time and if they're sharp you'll get cones having the right lengths, tapers and diameters for very little more money than you would spend just to buy the materials. Bent tubing, to be used in making the lead-in pipe, can be obtained in a variety of diameters and bend-radii at most muffler shops. Welding? Unless you have the equipment and are competent at welding light-gauge metal, that too should be hired from a professional, for the finished item can get to look very scabby given the best of workmanship. As for tolerances, the only thing you really must watch is that the fractions of an inch do not add up to upset the distance from the exhaust port window back to the baffle cone. An inch there, will move the power peak about 500 rpm. The same increment in length, up at the lead-in pipe, produces a slight reshaping of the entire power curve. Through most of the system, try to work to within ¹/₁₆-inch tolerances.

When testing the finished item (to recap some things already noted), remember that changing the taper of the baffle-cone changes that Dart of the - power curve past the power peak, while changes in the lead-in pipe length mostly influence the low-revs part of the curve. Increases in volume are effective mostly in adding area under the power curve right at the power peak; reducing outlet pipe diameter will, if the existing pipe is too large, boost power over the entire range, but requires that you keep a close watch over piston-crown temperature. There are other, more subtle things that may need correcting: for example, those oh-so-helpful sonic waves are not always content just to reverberate up and down the entire length of the expansion chamber. As it happens, each part of the system tends to develop its own individual resonances, and the lead-in pipe, diffuser, baffle-cone and outlet pipe will each have their own little wave system rattling back and forth, with other resonances of lower frequencies occurring in paired parts of the chamber. In most cases, these incidental wave patterns go unnoticed, but sometimes they will fall into mutually-reinforcing activity at certain engine speeds and combine to force humps and hollows into what would otherwise be a nice, even power curve. When these do occur, often a slight shifting on lengths is enough to keep them from marching locked-step and interfering with the job you are trying to do with the primary wave motions.

Far more common, when you fit an expansion chamber exhaust system on some engine intended for an unassuming muffler, is that the balance between the mixture delivered by the carburetor and the requirements imposed by conditions in the combustion chamber is destroyed. Regrettably, the high output two-stroke engine is to a very large extent gasoline-cooled, requiring rather more fuel mixed with its air than is needed to satisfy the simple chemical combination of oxygen and hydrocarbons in the burning process. In light of this, you will appreciate that an expansion chamber arranged to provide an enormous boost at some point along the engine speed range makes it absolutely impossible to jet the carburetor for clean running at all engine speeds. The way it works is that an engine's torque peak sets the mixture-strength requirement - with regard to cooling the piston crown below its melting point, squelching detonation, etc. - and if that mixture is too rich for lower, or higher, engine speeds, then the power range suffers. Sometimes, jetting for that torque peak will make the mixture so rich that the engine will hardly run at all in its low and middle ranges. There will be more on this subject in the chapters on carburetion and cylinder head design; it should be enough to say, here, that for truly broad range performance, it may be necessary to compromise in terms of expansion-chamber effectiveness to stay within the tolerances permitted by the mixture an ordinary carburetor will deliver. You can do that, and then take up some of the slack in engine performance with a higher compression ratio than you would dare use with an expansion chamber that gave a big narrow-range boost.

Two years ago, you wouldn't have been bothered with anything beyond the expansion chamber's outlet pipe; today, you'll have to fit a muffler, and it is important that you know what such an end-fitting means in over-all performance. Properly managed, the addition of a muffler to your expansion chamber will have absolutely no effect on power output, and will increase only slightly the exhaust system's size and weight. Trying to accomplish the same thing with a racing four-stroke engine would be difficult to the point of impossibility, but the two-stroke's expansion chamber must have a restricted outlet in any case, and it cares little whether the restriction is provided by a simple bit of pipe, or by a muffler. I have dyno-tested a number of expansion chambers, made as replacements for stock mufflers, that actually showed a gain in power with an add-on muffler. Of course, these chambers clearly had too-large outlet pipes, and the same result could have been obtained with pieces of smaller-diameter tubing. Still, it would be the same result, which means that there is no performance penalty to be paid when an expansion chamber's outlet pipe is capped with a muffler.

The only real problems you will encounter in muffling an expansion chamber exhaust system are: muffling effectively; and muffling without adding too much flow resistance. The latter problem is of minor importance if you have access to a dynamometer, but assumes critical proportions when you must rely strictly on seat-of-the-pants testing. Adding too much restriction, with the muffler, will produce precisely the same effect as when the outlet pipe is made too small: drastic overheating of the engine. Predicting flow-resistance through a muffler is very much more difficult than for a straight pipe, so the trick is to use a muffler that offers a straight-through passage for the exhaust gases, and a passage of such diameter that it will add little or no resistance to that already provided by the chamber's outlet pipe. With a muffler meeting that specification, the expansion chamber simply will not know that it isn't releasing its pulses straight into the atmosphere. There will be no special problem in finding that kind of muffler, as several manufacturers - their interest stimulated by the recent AMA rule requiring that all motorcycles in sportsman-class racing be muffled - are now producing straight-through silencers to spigot-mount on outlet pipes of various diameters.

This brings us to the problem of effectivesilencing, and I take no pleasure in telling you that none of the mufflers being offered for sale as this is written are particularly effective. They are, of course, better than nothing, but they will not reduce the noise output from your motorcycle down to even the 92 dbA maximum specified by the AMA's rule. Worse, most of them rely on fiberglass packing for their sound-damping properties - and this fiberglass fairly quickly disintegrates and is blown out with the exhaust gases, or loads with carbon and oil (which kills its ability to attenuate sound waves), or both. Only frequent replacement of the fiberglass packing will keep such mufflers in working order, and we may very shortly face federal regulations that specifically forbid the use of fiberglass in mufflers. And the same regulations probably will specify a maximum noise level for even off-road vehicles somewhat below the AMA's 92 dbA limit - a limit that is not now being met by fiberglass-packed mufflers in perfect working order.

These several difficulties should convince anyone that a different approach to the problem of effectively silencing the expansion chamber is required. Lacking a more effective solution to the problem, we may eventually be forced to revert to a straightforward muffler in place of the expansion chamber and live with the loss of power and performance that entails. I do not believe that will be necessary, as I stumbled upon a phenomenon a few years ago that meant very little at the time but now assumes major importance: The then-existing general racing regulations required that a motorcycle's exhaust system terminate at some point forward of the rearmost edge of the back tire, and I was planning to race a bike with its cylinders reversed to provide rear-facing exhaust ports (for reasons that were important, but not pertinent here). The only major flaw in this scheme was that even with the motorcycle built on a longish wheelbase and with its engine located well forward, there was not quite enough room for the exhaust pipes within the length allowed by the rules. The expansion chambers themselves would fit, but there was some 12-inches of outlet pipe left hanging back behind the rear tire, and not enough room to curl these outlet pipes back within the limit. While groping for a solution, I hit upon the idea of simply sliding them forward, inside the baffle cones. There, they would still function as pressure-bleed resisters, and further contemplation led me to the conclusion that the expansion chambers might even work better with their outlet pipes positioned inside. With the forward end of the outlet pipe located at the chamber's maximum diameter, ahead of the baffle-cone, there should be a somewhat stronger reflection from the baffle, and that might very well give the engine a somewhat better boost. Or so I thought.

Anyway, I gave the scheme a try, and while certain other modifications prevented drawing any absolute conclusions from the experiment, the bike did prove to be very fast, and it seemed certain that while my “inside stingers” might not offer any real power advantage, they probably were at least as effective as those attached in the more conventional manner. But that is not to say that I did not notice a difference - and the difference was in sound. With those inside outlet pipes, the typical expansion chamber crackle was very noticeably subdued. That made sense, as the chambers' outlet to atmosphere was taken from a point where the pulse was at its lowest amplitude - rather than from the high-pressure area at the tip of the baffle-cone.

More recently, I have been able to perform a series of tests using a dynamometer, to see if my inside-stinger idea (which, I had learned, was an idea also advanced by an obscure German researcher some several years earlier) had any real merit. An expansion chamber was constructed with its baffle-cone terminating in a clamp, to allow rapid changes in outlet pipes. and we tried pipes of different diameters and lengths, and moved them back and forth in the clamp to find the change in output as the outlet's forward end was advanced up the baffle-cone. The results were most interesting: There was absolutely no difference in power output with the outlet pipe in full-forward and full-back positions, but we did find a quite noticeable drop in power with the pipe's forward end pushed up to the approximately-halfway point in the baffle-cone. We also found that the same outlet pipe diameter produced optimum results no matter what the location, but that the system was rather less sensitive to outlet pipe length when the pipe's forward end was located an inch or so ahead of the baffle-cone's forward end. Finally, we found that the noise output with the forward-located outlet pipe was very much reduced: to about the same level as a conventional expansion chamber fitted with a bolt-on, fiberglass-packed muffler. I was, of course, a bit disappointed that my inside-stinger pipe did not show a big advantage in power over the conventional variety (there may be a slight broadening of the power curve, but the differences observed were too small to offer conclusive proof). Still, by that time, the sound-damping properties of the inside-stinger arrangement had become extremely important, as they could be used in conjunction with a low-resistance muffler, located farther downstream, to meet the AMA's new noise-limit rule without any loss of performance. For that reason, this idea - the creature, indirectly, of the AMA competition rules book - did prove to be a success, even if not in precisely the form I had anticipated.

Given the disadvantages of the fiberglass-packed muffler, better designs are needed and already are beginning to appear. Yamaha, for example, have quite an effective muffler for their expansion chamber-equipped motocross motorcycles. This one consists of a perforated tube passing through a canister, with the center of the tube plugged to force the exhaust pulses out through the perforations in the first half of the tubes and, into the canister, where they escape back through the holes in the tube's second half and then off into the atmosphere. Passage through the holes, which have diameters of about 5mm, breaks up the pulse, and it is further attenuated by expansion inside the canister. My only concern here is that Yamaha's new muffler may over-restrict the expansion chamber outlet, but given that company's thorough approach to engineering and testing, that seems a remote possibility. However -and this is not my concern, but the AMA's -I doubt that Yamaha's muffled motocrosser is really quiet enough to meet the AMA's 92 dbA limit. Perhaps so; perhaps not. In any case, the expansion chamber is here to stay, and so is the movement to restrict noise. The problems of effective muffling will be solved, and I think my inside-stinger may help with the solution.

EXPANSION CHAMBER DESIGN FORMULAE

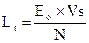
Where: L_t = tuned length, in inches

E_o = exhaust-open period, in degrees

V_s= sonic wave speed (use 1700 feet per second)

N = crankshaft speed, in revolutions per minute

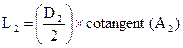
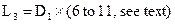
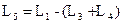
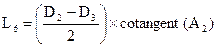
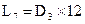
D_l = (see text)

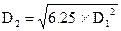
D₃ = D₁ x (0.57 to 0.62, see text)

A₁ = (half the diffuser's angle of divergence)

A₂ = (half the baffle-cone's angle of convergence)

USEFUL COTANGENTS:

cot 3.0^o = 19.0811

cot 3.5^o = 16.3499

cot 4.0 ^o = 14.3007

cot 4.5 ^o = 12.7062

cot 5.0 ^o = 11.4301

cot 5.5 ^o = 10.3854

cot 6.0 ^o = 9.51436

cot 6.5 ^o = 8.77689

cot 7.0 ^o = 8.14435

cot 7.5 ^o = 7.59575

cot 8.0 ^o = 7.11537

cot 8.5 ^o = 6.69116

cot 9.0 ^o = 6.31375

cot 9.5 ^o = 5.97576

cot 10 ^o = 5.67128

cot 11 ^o = 5.14455

cot 12 ^o = 4.70463

cot 13 ^o = 4.33148

cot 14 ^o = 4.01078

cot 15 ^o = 3.73205

CENTERLINE LENGTH OF CURVED PIPE

L = R x 0.01745 x angle of bend

Most of the literature dealing with the two-stroke engine's port timings makes a serious and fundamental error in concentrating on timing to the exclusion of everything else. In many instances very impressive-looking graphs will be presented, to illustrate how exhaust port timing, for example, will advance with increases in engine speed, etc., etc., but all seem to slip quietly past a couple of facts that should arrest everyone's attention: First, it should be clear to anyone who has made even a cursory study of the various two-stroke engines' port timings that no close correlation between these timings and engine speed exists. Second, it should be equally clear that the basic function of these ports - which is to permit a volume of gases under pressure to escape confinement - is not solely dependent upon time. Time is required, obviously, but the process is one that also is sensitive to area. In other words, at any given pressure differential the time required to move a volume of gases through a port in the side of a cylinder wall will be mostly a function of the port's cross-sectional area. Thus, it is not possible to treat with timing alone when planning the porting in a two-stroke engine; you must find the combination of time and area that will permit complete passage of the gas volume at hand.

This time-area requirement has been known to me a lot longer than I have been able to effectively quantify the concept. It is one thing to know that time-area numbers applicable to the whole range of two-stroke motorcycle engines probably exist, and quite another to find them. What I needed first was a mathematical expression that would combine the time factor with port area, and include an adjustment for the ratio between port area and unit cylinder volume. But while this might appear to be fairly simple, there is a serious difficulty in arriving at a value for port area. Just measuring the total port area would not suffice, for the port is fully open only for that infinitesimally brief moment when the piston rests at the end of its stroke; at all other time, during the period when a port is nominally open, some part of the port window is masked by the piston. Worse, the degree of masking varies to some extent according to differences in ratio between the on-centers length of connecting rod and stroke, and also with the absolute port-open duration. In consequence, any study of port time-area would have to be based on numbers not readily available unless one has endless hours to devote to collecting information either locked away inside the engines themselves or inside manufacturer's archives. It is possible to work out time-area numbers on a purely theoretical basis, but this approach is even more time-consuming, involving as it does some really nasty work with integral calculus equations. Also, this approach virtually demands that one make some fairly shaky assumptions in a number of areas -and that a computer be at hand if all the calculations are to be completed in this century.

All this changed when I acquired an SAE paper presented by Yamaha's Naitoh and Nomura. In this paper, time-area values suitable for two-stroke motorcycle engines are given, and while there was no explanation of how these were derived - particularly with reference to the determination of port area - they did provide the key that unlocked what had been a great mystery. While puzzling over the Naitoh-Nomura time-area values, I recalled that one of the pioneers in the field, Schweitzer, had based his calculations on a “mean” port area that was simply the aperture presented when the piston was halfway toward the fully-open position at the end of its stroke. That is to say, halfway in terms of degrees of crank-angle, and not where half the port is uncovered. For example, with an exhaust port that opens 90-degrees before bottom center, the mean port area would be taken with the piston 45-degrees of crank-angle from bottom center -which in most engines will uncover about 70-percent of the total port-window area. Assuming that Naitoh and Nomura were working along those lines, I worked out time-area values for a couple of Yamaha racing engines for which I had all the applicable data, and they fell neatly into place. Actually, the Naitoh-Nomura paper was rather obscure on this point and I was forced to do a lot of assuming, but it did provide a pattern in time-area relationships that, once unraveled and checked against concrete examples provided by Yamaha's engines, enabled me to present what I consider to be valid numbers.

SPECIFIC TIME-AREA

The numbers given here express time and area, and the ratio between port-window area and cylinder volume. They represent narrowly defined guidelines for intake, transfer and exhaust port time areas as follows:

For piston-controlled intake ports, 0.00014 to 0.00016 sec-cm²/cm³

For transfer ports……………….., 0.00008 to 0.00010 sec-cm²/cm³

For exhaust ports……………….., 0.00014 to 0.00015 sec-cm²/cm³

For rotary-disc intake valves,,,,,,,,, 0.00018 to 0.00019 sec-cm²/cm³

Some of you may not quite understand that expression, “sec-cm²/cm³”. It may look a trifle intimidating, but it merely indicates that the number preceding it was derived by dividing cylinder volume, in cubic centimeters (cm³), into the mean area in square centimeters (cm²) of the port in question, and then multiplying the resulting number by the total time, in seconds, during which the port is open. It says, in short, “time-area per unit displacement”, and it removes all the mystery that has so long surrounded port timing.

To work any time-area problem, you must first be able to convert an engine's timing, in degrees, into actual time at some given engine speed. Let us begin with a hypothetical exhaust port timing of 170-degrees duration, and an engine speed of 7000 rpm - the speed at which we intend that the engine should develop maximum power. To convert these known factors into time, we use the following formula:

Where, T is time, in seconds

N is engine speed, in rpm

is the port-open period, in degrees

Thus,

T = 0.004 seconds

Determining T, or time, is quite simple; the process of finding a port's “mean” area is somewhat more complicated and infinitely more time-consuming. There are two basic approaches to finding mean port area: The most direct is to simply bolt a degree-wheel to the end of the crankshaft, align it for TDC, then find the point at which the port begins to open and, finally, crank the engine over to a point halfway between the point of port-opening and bottom center (or top center, if the intake port is being checked). With the piston at that halfway mark, measure the area of the port window that is exposed and you'll have the mean port area - which represents the average size of the port-window aperture through the whole period from opening to closing.

The second method for finding mean port area, and the one I prefer, is to transfer all of the pertinent dimensions to a sheet of fine-grid graph paper and work from that. Begin by drawing a vertical line to represent the cylinder axis and then, toward the bottom of that line, add a circle representing the path followed by the crankpin. With that done, measure up from the top of the circle a distance equal to the on-centers length of the connecting rod and add a horizontal line at that point. Repeat this, measuring from the bottom of the circle, and you have created the space swept by the piston. The ports are then drawn in, flanking the line that represents the bore axis, with the exhaust and transfer ports down against the bottom of the space and the intake port situated up at the top. Finally, mark the mean port-open points on the circle, using a protractor, and connect these points and the bore-axis line with lines of precisely the length of the connecting rod, center to center. You will find that the connecting points, on the bore-axis line, fall about 70-percent down on the exhaust port, about 75-percent down the transfer ports (of which only one side need be shown) and about 65-percent up on the intake port. Draw horizontal lines through the port windows at these points, and you'll then be able to measure the mean open areas… assuming that you have accurately reproduced all the dimensions.

Time-area studies may be made directly from an engine, but a better method is to transfer the appropriate crank, rod, and port dimensions to a sheet of graph paper, then take mean port areas from the drawing.

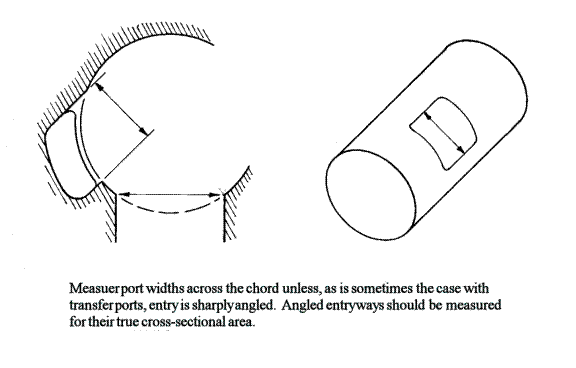
You will find that the most difficult job is to accurately reproduce the port window shapes. Exhaust ports tend to be more nearly round than square in high-output engines with wide, un-bridged ports; intake ports have rounded sides even when they are basically rectangular; transfer ports often have \ angled upper edges; and in addition to these difficulties, you must determine accurately the radii existing at the corners of all ports. So, finding the area of a given port aperture is not simply a matter of multiplying width times height. My own method for resolving this difficulty is to make a close-fitting paper sleeve, slide it inside the cylinder being checked, tape it in place and then, by rubbing around the edges of the port windows with the side of a pencil tip, transfer the window shapes to the paper. Please understand that these shapes may not then be transferred directly to the graph paper on which the bore, connecting rod, and crankshaft lines have been drawn. Why? Because in laying the sleeve flat, the width of the ports is exaggerated, and what you need is the true size of the aperture. My approach is to make this paper cylinder out of fairly stiffish stock, and after getting the port shapes marked on its inner surface to reverse its sides, creating a cylinder with the port window drawn outside where they can conveniently be measured with precise calipers and the true dimensions then transferred to my working drawing. A series of horizontal guide-lines drawn across the port shapes before re-rolling the cylinder is an aid in measuring the port's shape, but in the final analysis accuracy depends on one's willingness to be meticulous with all measurements and to be imaginative in concocting ways of recreating a port shape on paper. I have found that a draftsman's ellipse template is very useful in this kind of work, but it is only essential that you have a good protractor, a straight-edge, a compass, and a supply of fine-grid graph paper. By assigning a value of one-millimeter per line, and doing all drawing to scale, you can not only work with considerable accuracy, but the determining of window areas become much easier - you just count the number of squares and fractions of squares within the “mean” aperture to get area, and if you have drawn everything carefully, the margin of error will be too small to be of any particular significance.

Having found the ports' mean areas, you are ready to complete your calculations in finding each port's value in sec-cm²/cm³. For an example, we'll return to the hypothetical exhaust port for which we have a port-open duration (derived from 170-degrees and 7000 rpm) of 0.004 sec. We will further assume that this port has a mean area of 8.0 cm², and is in a cylinder having a displacement of 250 cm³ (or, as it is more commonly expressed, 250cc). To arrive at the figure we want, in sec-cm²/cm³, it is first necessary to divide cylinder volume, 250 cm³, into port area, 8.0 cm², and then multiply the results by time, in the following manner:

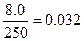; 0.032 x 0.004 = 0.00013 sec-cm²/cm³

And, referring back to the specific time-area figures already provided, which establish a range from 0.00014 to 0.00015, we learn that this particular hypothetical engine is time-area deficient, in the order of 10-percent. Increasing the port width, to bring the mean open area up to 9.0 cm², will raise the exhaust port's specific time-area to 0.000145, which is right in the middle of the specified range. Increasing this engine's exhaust-open duration will increase both time and mean area, and that's where the drawing on the graph paper becomes very handy, as it enables you to chart how much area is gained by increases in timing, and to establish what combination of port width, height and timing will yield the specific time-area need for the particular engine with which you are working. In most instances you will not be able to obtain the correct values by merely widening ports; a combination of increases in both time and area are required if your stock engine has a power peak at, say, 6000 rpm and you want to push it a thousand or so rpm higher.

ANGLE-AREA

With all the juggling of numbers entailed in finding correct combinations, it is advisable to find short-cuts, and one of these is to work with specific angle- area numbers instead of time area. One cannot simply substitute angle-area for time-area and ignore the engine speed factor, obviously, so I have provided charts from which you may work. Take, for instance, the exhaust port time-area/angle-area chart: you'll find that there are two line marking the exhaust time-area limits of 0.00014 and 0.00015 sec-cm²/cm³, with vertical lines marking off engine speed and horizontal lines for angle-area. The specific angle-area of our hypothetical example, taking the exhaust-open duration as 170-degrees and the cm²/cm³ figure as 0.032 (8.0/250), is 170 x 0.032 = 5.44 deg-cm²/cm³. Referring to the chart, we note that at 7000 rpm the specific angle-area requirement is from about 5.88 to 6.3 deg-cm²/cm³, meaning that more time and / or area will be needed if the engine is to operate effectively at 7000 rpm - and that an angle-area value in the order of 6.1 deg-cm²/cm³ is a good target figure. This process is, of course, intended to be repeated for all of any given engine's ports.

These time-area and angle-area numbers are enormously useful in planning the porting of any two-stroke motorcycle engine, and I would be happy to tell you that they represent the final word on the subject… but they unfortunately do not. Many other factors intrude upon this seemingly uncomplicated picture: Referring once again to the time-area/angle-area charts, you will observe that there is, in every instance, a range for what constitutes correct values, which reflects the fact that the optimum is influenced somewhat by factors beyond those already discussed. Sadly, it is in accounting for these that we must depart from the comfortable certitudes of mathematics, for the other influences are in the field of exhaust system design and characteristics, flow coefficients, nominal and effective port areas, crankcase compression ratios, resonance in the intake tract, and very likely a host of minor influences that will forever escape our attention. All these add up to a situation in which a certain amount of adjustment, done according to results observed in testing, will always be necessary. Calculation brings us close to the optimum, after which we work within the time-area/angle-area range according to an educated guess, and finally we test. Professional engineers do not do the job any differently.

Date: 2015-12-17; view: 3448