
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
PISTON ACCELERATION
PREDICTING POWER
An average, well-developed stock engine intended for use in a sports / touring motorcycle will have a bmep of about 70 psi. It is possible, and I must stress that word "possible", to raise this to perhaps 115 psi- an improvement of some 64-percent, which (if accomplished) will yield a 64-percent increase in power output without raising the engine's operating speed. Similarly, a 64-percent increase in operating speed without a change in bmep would have the same effect on output. You will see this in the following formula for calculating horsepower:
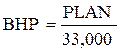
Where BHP is brake horsepower
P is brake mean effective pressure, in psi
L is piston stroke, in feet
A is the area of one piston, in square inches
N is the number of power strokes per minute
Obviously, when the values of L and A are held constant, as would be the case with an engine having a piston displacement at the limit established for a particular racing class, then increases in power may only be obtained by increasing the values for P and N -and you will find that in practice it is a lot easier to increase the latter than the former.
As already stated, bmep figures for stock, touring-type engines with flow-restricting air cleaners and mufflers, and with porting / carburetion compromised in favor of smooth low-speed running, will be around 70 psi. Typical figures for engines with porting and other plumbing arranged solely (and effectively) for maximum horsepower at peak revs would be about 115 psi - with a few small, highly-developed two-stroke engines operating up at 125 psi. The exact number will vary according to unit cylinder displacement and the width of an engine's useful power band, but one may reasonably expect that engines suitable for motocross will fall in the 85-95 psi range - with big cylinders tending toward the lower figure and small cylinders vice versa.Road racing engines, tuned to exert a maximum effort over a very narrow speed range, will usually show a bmep of 100-115 psi, and of course the same remarks regarding the influence of cylinder size apply.
These numbers have a usefulness beyond the mere satisfaction of vulgar curiosity: they may be used very profitably to determine an engine's suitability for some particular application. For example, they shed light on the future prospects of those who are trying to transform Kawasaki's F-5 “Bighorn” engine, a 350cc single, into a prime-mover capable of ending the Yamaha TD-2's absolute domination in road racing. Much has been made, by the Kawasaki's supporters, of the usefulness of a broader power range inherent with the F-5's disc-valve induction and the l00cc advantage it gets, over the TD-2, by having only a single cylinder (this, under the present American Motorcycle Association rules). Now while it is true that a racing motorcycle having a wide power band is easier for its rider to manage, and may offer an absolute if very slight advantage on short, extraordinarily twisty circuits, one must not overlook the fact that the TD-2 has been blessed with an excellent close-ratio transmission and a number of riders quite capable of coping with any problems introduced by the need for frequent gear changes. Viewed realistically, the situation facing any serious challenger to Yamaha's supremacy is one in which horsepower must be met with horsepower. And what are the Kawasaki's prospects of developing that kind of horsepower? Let's have a look at the numbers:
Assuming that the man who modifies the Kawasaki F-5 knows his business, but doesn't have all the development time in the world, (probability favors the latter far more than the former) then he very likely will arrive at a combination of porting, etc., good for a bmep of about 105 psi-which is about all that can be expected with a single cylinder of 350cc displacement. To expect more would be to ignore the considerable difficulties in scavenging efficiently the F-5's large-bore (3.17-inch) cylinder. Further assuming (and as we shall see later, this assumption is far from safe) that the F-5 engine will remain in one, working piece for the duration of a longish race with its rider observing a red-line of 9000 rpm, with a power peak at 8500 rpm, then,
BHP = 
BHP = 47.6
So, a well developed F-5 would deliver 47.6 brake horsepower. How does that compare with the Yamaha TD-2? With all the years that have gone into the TD-2's development, and giving due thought to Yamaha's proven expertise in these matters, it seems safe to assume that this engine would be operating with a bmep of 115 psi at its power peak- which seems to be at 11,000 rpm. Thus, working from those numbers and the 250cc Yamaha twin's bore/stroke dimensions of 56mm and 50mm, respectively,
BHP = 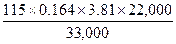
BHP = 48.0
Clearly then, those who would try to beat the Yamaha with a Kawasaki F-5 have taken upon themselves a task of considerable magnitude. The only bright spot in the picture, for them, is that while they are 0.4 bhp down on the Yamaha (assuming near-optimum work on their part) they probably will have the advantage in terms of average horsepower, figured from the moment a gear is engaged - when revs fall somewhat below those for peak horsepower -until the red-line is reached and it is time for a change to the next higher gear. There will be no advantage in frontal area, for although the F-5 engine is narrower than that of the TD-2, the fairing must be wide enough to shroud the rider, and the minimum width that requires is sufficient to encompass either engine. Moreover, moving from the theoretical to the practical for a moment, it is highly unlikely that the Kawasaki could be made as reliable at 8500 rpm as is the Yamaha at 11,000 rpm, and not because the F-5 engine is badly designed or shoddily constructed. The simple truth is that any single-cylinder 350cc engine with the F-5's bore / stroke dimensions and red-lined at 9000 rpm is going to be stressed very near its absolute limit - a limit imposed by the properties of available materials.
PISTON SPEED
All this asks the question, “How does one determine the limit, with regard to engine speed?” Unfortunately, establishing this limit with any precision is not only extremely difficult in terms of the mathematics involved, but also requires data concerning metallurgy, etc., seldom available outside the record-rooms of the factories from which the engines originate. Still, there are guide-lines which, if lacking in absolute precision, do at least have the virtue of simplicity, and will provide an indicator to keep us away from certain trouble. It is almost impossible to establish the point, in engine speed, between zero trouble and the possibility of trouble; there is much less difficulty in determining a red-line between sometrouble and nothing but trouble.
A quick and easy method of establishing a limit for crankshaft speed is by working with piston speed. Actually, with "mean" piston speed: pistons do not travel at uniform velocity; they move from a dead stop at each end of their stroke, accelerate up to a maximum speed that often is in excess of 120 mph, and then brake to another complete stop. For convenience, we use just the mean piston speed and the safe limit for that, for engines having bore-stroke dimensions within the range considered normal for motorcycles, is about 4000 feet per minute. And mean piston speed may be calculated very easily by applying the following formula:
Cm = 0.166 x L x N
Where: Cm is mean piston speed, in feet per minute
L is stroke, in inches
N is crankshaft speed, in revolutions per minute
Thus, using again the Kawasaki F-5 engine as an example, with L being 2.68-inches and N given as 9000, we find that
Cm = 0.166 x 2.68 x 9000
Cm = 4000 ft/min
Here we have a theoretically-predicted limit that seems to agree quite closely with observable reality in the field: Reports from those actually racing modified F-5 Kawasaki’s indicate that the engine does in fact retain acceptable (within the framework of that word's meaning in racing) reliability when red-lined at 9000 rpm, and ravels with horrifying abruptness if pressed further. Of course, it must bestressed here that few engines, the F-5 not excepted, retain more than marginal reliability at mean piston speeds of 4000 ft/min, and even this presupposes frequent replacement of the piston and the crank/rod bearings.
You will be on far more solid ground if your engine is not asked to enduremean piston speeds above 3500 ft/min. Anything above that takes an engine into the twilight zone of reliability, and the ground between 3500 ft/min and the near absolute limit of 4000 ft/min is covered with unpleasant possibilities, but these often may be minimized with the proper selection of materials and lubrication. I should note here that there are exceptions to this rule among some of the old-fashioned, long-stroke engines, which tend to have very light (and strong) reciprocating parts relative to their absolute stroke. An example that comes to mind is the Bultaco 125cc TSS, which had a stroke of no less 2.36-inches (decidedly long for a 125) but which would, in “factory”road racing trim run up to 11,500 rpm, just like the Yamaha TD-2 (with a much shorter, 1.97-inch stroke), and that represents a mean piston speed of 4500 rpm. Obviously, Bultaco held the opinion that the resulting thin-ish margin of reliability was acceptable, but their TSS never was as predictably trouble-free as Yamaha's TD-2, which at the same crankshaft speed (11,500) has a mean piston speed of only 3775 ft/min.
While on the subject of bore/stroke dimensions, I would like to say that there is much in favor of long stroke two-stroke cycle engines in many applications. They are not superior (as many people seem to think) compared to the present day short-stroke designs in terms of low-speed torque, as torque is entirely a function of displacement and bmep, and wholely unrelated to bore/stroke ratios. With a long stroke, there is (at any given displacement) a reduction in bore, and with it a loss of piston area against which gas pressure can exert its force, that exactly balances the loss of leverage in a short-stroke engine (which is, in turn, compensated by a gain in piston area). The only thing wrong with the long-stroke engine is that its crankshaft speed is limited by inertia loadings, and that in turn limits its absolute power potential as compared with the “modern” short-stroker. On the other hand, it is compensated by having a much more compact combustion chamber, which makes for more efficient burning, and by lower thermal loadings on the piston as a result of the smaller crown area into which heat from the combustion process may soak. Finally, there is an advantage in port area for the long-stroke design resulting from its relatively large cylinder wall area. This area increases in the long-stroke engine because displacement rises only in direct proportion to stroke, but is increased by a factor of 3.14 (the constant, pi) with enlargements in bore. These are very real advantages, but they are not enough, usually, to prevail against the short-stroke engine's sheer ability to rev. Crankshaft speed is the only thing subject to much juggling in the horsepower equation- and is a far more potent factor in determining power output than the relatively slight improvements in bmep obtainable with the marginally better combustion chamber and porting in the long-stroke engine. A 10-percent improvement in our Kawasaki F-5 engine's bmep (a large improvement indeed) would raise its output to 52.3 bhp; leave the bmep unchanged, but shorten the stroke and spin it 11,000 rpm and you would have 61.3bhp. There is indeed no substitute for revs.
PISTON ACCELERATION
Sadly, while there is no substitute for revs, there are plenty of barriers: piston speed is one, as was already noted. But that is a rather indirect limit, as it ignores the fact that it is not speed so much as all the starting and stopping of pistons that does the damage, or at least the worst of any damage. The acceleration forces generated by the starting and stopping are felt even in an engine's main bearings, but they are at a peak in the connecting rod and piston and have a particularly disastrous effect on the latter, as any attempt to make a piston stronger is apt also to make it heavier-which aggravates the very situation the strengthening of the piston should improve. Even so, an engine's true Achilles heel, the problem that may most strongly resist solution, often is the disastrous effects piston acceleration may have on the piston's rings.
It often is thought, and quite wrongly, that rings maintain a seal between the piston and the cylinder's walls simply through their properties as springs. Alittle thought should convince you that such cannot be the case, for most rings, compressed in the process of installation, press outward against the cylinder with a force amounting to about 30 psi. Gas pressure in that cylinder may easily exceed 750 psi, and it should be obvious 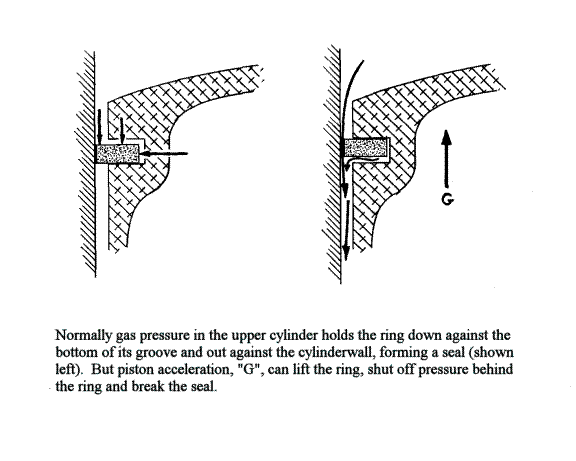 that a 30 psi force will not hold back one circa750 psi. Still, equally obviously, piston rings do form an effective seal. How? Because they get a lot of help from the cylinder pressure itself: gas pressure above the ring forces it down against the bottom of its groove in the piston, and also (acting behind the ring, in the back of the groove) shoves it out hard against the cylinder wall. Thus, in the normal course of events, sealing pressure at the interface between cylinder wall and ring always is comfortably higher than the pressure it must hold back.
that a 30 psi force will not hold back one circa750 psi. Still, equally obviously, piston rings do form an effective seal. How? Because they get a lot of help from the cylinder pressure itself: gas pressure above the ring forces it down against the bottom of its groove in the piston, and also (acting behind the ring, in the back of the groove) shoves it out hard against the cylinder wall. Thus, in the normal course of events, sealing pressure at the interface between cylinder wall and ring always is comfortably higher than the pressure it must hold back.
This very desirable situation will be maintained unless something happens to upset things, and most-insistent among the several “something’s” that may intrude is excessive piston acceleration. When piston acceleration exceeds the sum total of gas pressures holding the ring in place, the ring will lift upward (as the piston nears the top of its stroke, and is being braked to a halt). Instantly, as the ring lifts, the gas pressure previously applied above and behind is also applied underneath the ring, at which point its inertia takes over completely and the ring slams up hard against the top of its groove. This last action releases all pressure from behind the ring, leaving it entirely to its own feeble devices in holding back the fire above, and as its 30 psi outward pressure is no match for the 750 psi pressure in the upper cylinder, it is blown violently back into its groove. The ring's radial collapse opens a direct path down the cylinder wall for the high temperature and pressure combustion gases-but only for a microsecond, for the action just described instantly applies gas pressure once again behind the ring and that sends its snapping back into place against the cylinder wall. Unhappily, it cannot remain there, as gas pressure immediately bangs it back into its groove again- to repeat the process over and over until the piston is virtually stopped and the ring's inertia is no longer enough to counter gas pressure.
The net result of all this activity is that over the span of several degrees of crank rotation, immediately preceding the piston's reaching top center, the ring will be repeatedly collapsed radially and at the same time hammered hard against the top of its groove. Understandably, the ring is distressed by this, as it not only receives a fearful battering but also is bathed in fire while being deprived of the close contact with piston and cylinder that would otherwise serve to draw off heat. Equally damaging is that the piston is having much the same problem, with high-temperature gases blowing down past its skirt to cause overheating, to burn away the film of oil between itself and the cylinder wall, and with its ring, or rings, all the while trying to pound their way up through the piston crown. A mild case of what is quite accurately termed “ring flutter” eventually results in the destruction of the ring and sometimes the dimensional integrity of its groove; a more serious case is certain to lead rapidly into lubrication failure, overheating, and piston seizure. Fortunately, this drastic problem can be avoided, thanks to the work of the researcher Paul de K. Dykes, whose investigation of the ring flutter phenomenon yielded most of what we know about it - and who invented the flutter-resistant ring that bears his name. Dykes showed us the cause of ring flutter, and engineers' understanding of the cause is reflected in their designs of the modern piston ring, which is very thin, axially, with a very considerable width, radially. Thus, gas pressure bears down on a large surface, providing an equally large total down-force, but is opposed by a relatively small upward load as the ring, being thin, is light and in consequence has little inertia. Still, even with very thin rings, flutter will occur if inertia loadings are high enough. To settle the question, with regard to any given engine, apply the following formula for determining maximum piston acceleration:
G max = 
Where G max is maximum piston acceleration, in feet per second squared
N is crankshaft speed, in revolutions per minute
L is stroke, in inches
A is the ratio of connecting rod length, between centers, to stroke
To illustrate how high these forces may sometimes be, let's use as an example the Yamaha TD-2, using 11,000 rpm for N. The formula tells us that at that speed, maximum piston acceleration will be (with the answer rounded off by my slide rule; I'm too lazy to do it all with paper and pencil) no less than 135,000 ft/sec2. Now if you will recall for a moment that the acceleration of gravity is only 32 ft/sec2, it will be clear that the load on the Yamaha's pistons - and thus on its rings - is very high indeed. But is the loading high enough to make the Yamaha's rings flutter? Obviously, it is not, as the engine remains not only reliable but crisp in comparatively long races. The limit, for the TD-2 engine, is slightly higher than 135,000 ft/sec2 - but not much higher, asyou will see in the following table listing ring thicknesses and the accelerations at which they begin to flutter.
For rings having a 0.125-inch thickness, 40,000 ft/sec2
0.094 “ “ 53,000 ft/sec2
0.063 “ “ 80,000 ft/sec2
0.047 “ “ 106,000 ft/sec2
0.039 “ “ 138,000 ft/sec2
The Yamaha, with rings having a thickness of 1mm, or 0.039-inch, and a maximum piston acceleration of 135,000 ft/sec2 at 11,000 rpm, would seem to be operating very near the limit - as indeed it is. But it probably is not quite as near the limit as the numbers suggest, for a racing ring (with its exaggerated thickness/width cross-sectional aspect) is somewhat less subject to flutter than a ring made for application in a touring engine. Still, the numbers given are fairly close for rings with normal-range proportions, and if you have an engine with rings for which Butter is predicted at 80,000 ft/sec2 and intend using crankshaft speeds that would raise maximum piston acceleration to something more like 100,000 ft/sec2, then I strongly urge you to fit new pistons with thinner rings. You may interpolate between the figures given to find the safe acceleration levels for ring thicknesses not listed.
There are piston rings that resist very strongly piston acceleration's efforts toward making them flutter. The best known of these is the Dykes-pattern ring, which has an L-shaped cross-section and fits into a similarly-shaped groove in the piston. The Dykes ring is made flutter-resistant by the fact that its horizontal leg fits quite closely in its groove, as compared to clearances around the vertical leg, and therefore even if acceleration lifts the ring it cannot lift high enough to close off the pressure behind the ring's vertical leg. In consequence, the ring's sealing abilities are maintained at accelerations that would be the undoing of rings in the conventional rectangular-section pattern. However, the Dykes ring's ability to maintain a seal does not free it of all the unpleasantness attending too-high piston acceleration: while it may seal under those 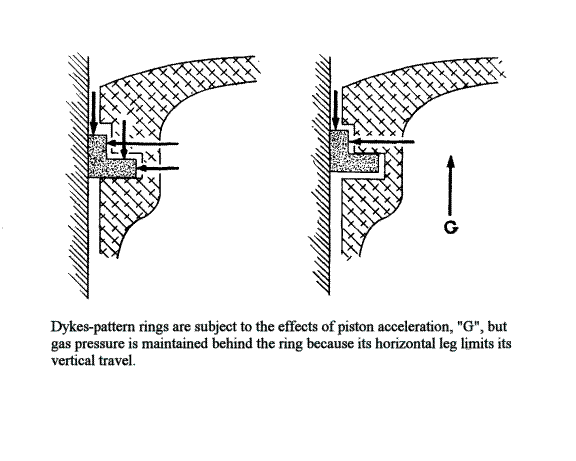 conditions, it is still being rattled about vigorously and if the rattling continues long enough, the Dykes ring, and the groove trying to restrain it, both become badly battered. At that point, its ability to seal vanishes and mechanical failure of the ring, piston, or both, follows very closely. Bultaco has long used Dykes-pattern rings, as have certain others, but most manufacturers prefer rings that do not require such careful and intricate machining. There are other flutter-resistant rings, and many excellent reasons for using rings of conventional configuration, but these details are discussed elsewhere in this book and in greater depth than would be appropriate here.
conditions, it is still being rattled about vigorously and if the rattling continues long enough, the Dykes ring, and the groove trying to restrain it, both become badly battered. At that point, its ability to seal vanishes and mechanical failure of the ring, piston, or both, follows very closely. Bultaco has long used Dykes-pattern rings, as have certain others, but most manufacturers prefer rings that do not require such careful and intricate machining. There are other flutter-resistant rings, and many excellent reasons for using rings of conventional configuration, but these details are discussed elsewhere in this book and in greater depth than would be appropriate here.
After establishing all these mechanical limits, with regard to piston speed and acceleration, and after deciding how much power you are likely to get from a particular engine, you should subject the engine to a complete survey. This would include the measuring of port heights and widths, combustion chamber and crankcase volumes, and charting piston travel against crank rotation. This last effort may at first seem rather pointless, but as your work progresses you will find that the chart, which will show almost but not quite a sine curve, provides an instant readout between degrees at the crankshaft and the position of the piston from top center that is most useful. It will tell you, for example, how much to raise the top edge of an exhaust port to make a given change in timing, and how much to trim from the piston skirt (in a piston-port engine) to get the intake period you want-or think you want. The chart also will provide you with all the mean port-open points, and it will provide an exceedingly useful relationship between ignition timing expressed in degrees and in piston travel from top center. You may devise your own methods for deriving all this information according to your preference and resources; I have explained my own techniques elsewhere in this text, in the appropriate chapters.
An item that must be included in any discussion of the two-stroke cycle engine's basics is general gas dynamics. You can get information on the subject at your local library, but the applicable particulars are likely to be widely scattered there, so I will cover the subject in brief here. The manner in which what follows applies at specific points throughout the engine and its related plumbing will be covered later, but you should know a few of the fundamentals now and thus save me from becoming unnecessarily repetitious later.
One thing you must know, for example, is that the air moving through the engine, a mixture of gases, has many of the properties of a fluid. It even has the ability to “wet” a surface, and has viscosity, which means that air will cling to all surfaces within an engine in a layer that moves hardly at all no matter what the midstream velocity may be. This boundary layer's depth is influenced by gas temperature, and by the temperature of the surface on which it forms, as well as by the shape of the surface. Please understand that the layer is not solid; it is “shearing” with general flow throughout its depth – which may be as much as 0.100-inch - with movement increasing as to distance from the surface on which it is formed. And as close as 0.020-inch from the surface, flow may still be in the order of 80-percent of that in midstream, which means that the restriction formed by the boundary layer is not very great. Nonetheless, it is there, and it accounts for such things as round ports having less resistance to flow than square ports, area for area, and for the ability of a single port to match the flow of a pair of ports of somewhat larger area. It also accounts for the fact that flow resistance increases in direct proportion with the length of a port, and much of the resistance resulting from the shape of a particular port is due to that shape's creating a thick boundary layer, which becomes literally a plug inside the port.
Generally speaking, boundary layers will be held to minimum depth on surfaces that “rise” (relative to the direction of flow) and gain in thickness on any surface that falls away. Thus, an intake trumpet, for example, should be tapered in slightly from the inlet end to the carburetor-by perhaps 2-3 degrees - in the interest of holding boundary layer thickness to a minimum. In that configuration, it will have appreciably less resistance to flow than a straight, parallel-wall tube. Similarly, transfer ports should diminish in cross-sectional area from their entrance in the crankcase toward their outlet in the cylinder.
These gases also have inertia: once set in motion they tend to remain in motion; when at rest they resist all efforts to get them moving. In practice, this means that there always is a lag between the intake port's opening and the movement of air in the intake tract. Fortunately, this lag can be amply compensated toward the end of the intake period, when the pressure inside the crankcase has risen to a level that should push part of the charge back out the port-but cannot because of the effect of inertia on the incoming gases. Inertia also has its effect on the flow of gases through the transfer ports and out the exhaust system, but I will deal with that while treating those subjects separately.
These inertia effects are useful, but difficult to manage as something apart from other processes occurring as the engine runs. For example, intake tract length usually is established more with an eye toward resonances than inertia, and its diameter set by the flow rate required by the carburetor to meter properly - balanced against the resistance that attends high gas velocities. Therefore, virtually the only thing we can do about inertia effects is to attempt to find the intake timing that will make maximum use of those provided by an intake system proportioned mostly to suit other requirements.
Resonances are another matter. Sound waves will travel through any elastic medium, such as air, and in their passage they pull together or force apart molecules, just as the similar energy waves traveling through the ocean pull the water into peaks and troughs on its surface. And, as in the ocean, the waves move steadily onward away from their source but the transmitting medium does not. Take, for example, the activity surrounding a single condensation, or positive-pressure wave, as it moves through the air. In its center, molecules have been pulled together, condensed, but as it travels it releases those molecules and compresses others as it reaches them. In the same manner, a rarefaction, or negative-pressure wave, pushes molecules apart. Both waves behave in a curious, but useful way when confined in a tube and the effects of inertia are mixed with them. For one thing, they will be reflected back when reaching the end of the tube - whether that end is open or closed. But at the tube's open end, the wave changes in sign: a condensation is inverted and becomes a rarefaction, and vice versa; at the closed end, the wave will be reflected, but retains its sign.
How is all that useful? For example, in the intake system the opening of the intake port exposes the crankcase end of the tract to a partial vacuum, and that in turn sends a rarefaction shooting off toward the opposite, atmospheric, end of the tract. It travels out to the intake bell, inverts in sign to become a condensation, and instantly moves back toward the crankcase - to arrive there as a clump of compressed molecules, which surge into the crankcase to be trapped, if the piston then closes the intake port, as part of the scavenging charge. That effect, over-layed with inertia in the inrushing gases, makes all the difference in getting the job of charging done in two-stroke engines – which provide only an absurdly short time for such chores.
How short a time? That is at the same time one of the least complicated and most depressing calculations you can perform. Let us consider the Yamaha DT-1, which in fully developed configuration had an intake duration of 160-degrees, a transfer duration of 123-degrees, and an exhaust duration of 172-degrees. Yamaha claims a power peak at 7000 rpm. Let's have a look at the actual time, in fractions of a second, available for the completion of these functions. To arrive at these times, use the following formula:
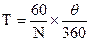
Where T is time, in seconds
N is crankshaft speed, in revolutions per minute
 is port open duration, in degrees
is port open duration, in degrees
(This formula can be abbreviated to  )
)
Thus, to find T for the 160-degree intake duration,
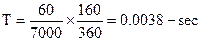 .
.
With application of the same formula to the transfer and exhaust periods, we find that the former is open 0.0029-second, and the latter open 0.0041-second. Even the longest of these, the exhaust-open duration, is only 41/10,000-second, and that is not very much time in which to empty exhaust gases out of the cylinder. Actually, that particular process is substantially finished in the 29-degrees, or 0.0007-second, between exhaust- and transfer-opening. In that short period, pressure in the cylinder must fall to something very near atmospheric, or the exhaust gases would force their way down into the crankcase through the transfer ports. Of course, the exhaust gases are provided quite a large aperture by means of which they may make their escape, and that they do so, successfully, is less remarkable than the fact that the fresh charge compressed in a two-stroke engine's crankcase is able to make its way through the far more restricted transfer ports, propelled by a far lower pressure, to refill the cylinder in the extremely brief moment available. It seems nothing short of astonishing that this recharging operation is accomplished in the 0.0027-sec provided by the Yamaha DT-1's 114-degree transfer period; that the same process takes place in a Yamaha TD-2 engine in only 0.0017-sec appears a minor miracle. Obviously, divine intervention is not really a factor in the functioning of two-stroke engines, and cylinder recharging is possible simply because the process gets a lot of help from the activities of the exhaust system, gas velocities through the transfer ports have a mean value in the order of 300 ft/sec, and the cross-sectional areas of the ports involved are relatively large as compared with the volume of gases to be transferred.
As it happens, it is possible to calculate correct combinations of port-open times and port areas for any motorcycle engine, at any engine speed. The maximum safe speed for any engine is also calculable, as explained earlier in this chapter, along with expansion chamber dimensions, carburetor size and many other factors influencing both maximum power output and overall power characteristics. It should be noted here that none of the values derived purely from calculations are necessarily optima, and fine adjustments must always be made experimentally, but it is far better to employ the simple formulae presented in the chapters to follow than to attempt a purely-experimental approach. The mathematics involved are not terribly complicated, though sometimes the arithmetic is laborious, and you can use paper and pencil to arrive at a basic engine/pipe combination that will be very near the optimum. Much nearer, in fact, than would be obtained by even the most experienced tuner's unsupported guesswork, and near enough to a fully developed configuration to minimize the outlay of time and money entailed in the building of a racing engine. You start by determining, mathematically, an upper limit for engine speed, then use more math in establishing a maximum for piston-ring thickness, in establishing all the port dimensions to suit the projected engine speed, in selecting a carburetor, and in designing an expansion chamber. Suitable values for compression ratios, both primary and secondary, are provided in the chapters dealing with crankcase pumping and cylinder heads, respectively, and with the rest of the material included in this book it all adds up to being a fairly complete engine redesign manual for the two-stroke engine-fixated “tuner”. My own experience indicates that engines built along the lines suggested here never fail to deliver high specific horsepower (which is more than may be said for any cut-and-try system) even without the benefit of experiment-indicated adjustments. I dislike guesswork, have made a serious effort to eliminate it from my own projects, and am hopeful that the lessons learned - and outlined in this text - will reduce the generally high level of guesswork among most experimenters. If I have forgotten to cover anything, the omission is inadvertent, because my distaste for Speed Secrets is even greater than for guesswork. There is only one “Secret” in the game: to know what you are doing, and to do it thoroughly.
As was noted in the chapter of this book dealing with basics, power output from an engine of any given displacement is a function of gas pressure in the cylinder during the power stroke, and the number of power strokes per unit time. Implicit therein is the suggestion that the horsepower ultimately to be had from an engine has little to do with port shapes and port timings, exhaust systems, carburetion or indeed any of the things on which our attention usually is fixed. Why? For one thing, increases in gas pressure bring corresponding increases in heat flow into the piston -and no high-output two-stroke engine can operate beyond its thermal limit. Similarly, you cannot increase the rate at which power strokes occur without increasing crankshaft speeds, with increases in this direction sooner or later taking you beyond the engine's mechanical limit. The horsepower you ultimately will extract from any given engine depends therefore very directly upon your ability to expand those thermal and mechanical limits to the greatest extent possible, and only then to make the most of the territory thus gained.
THE PISTON
For a very long time subsequent to Dugald Clerk's creation of the two-stroke engine, the thermal limit was the only limit, but it was enough to hold power output from such engines to extremely modest levels. Then, as now, it was primarily a limit imposed by available piston materials. Cast-iron has its advantages in terms of wear resistance, hot-strength and low thermal expansion rates, and it was used quite frequently in the low speed engines of years past. Unfortunately, iron is heavy, and heavy is the last thing you want in a piston - which in modern engines is subjected to accelerations well in excess of 100,000 ft/sec2. Aluminum, used as the primary constituent in virtually all piston alloys today, is conveniently light, but disagreeably insists on melting at much lower temperatures than that of the fire to which it is directly exposed. Moreover, it loses strength very rapidly with increases in temperature above ambient, so that piston failures do occur at crown temperatures well below the material's melting point. Finally, aluminum is a high expansion-rate metal, which makes a piston made of it a variable-clearance fit in any cylinder. But aluminum is a very light metal, and that alone was enough to recommend it for use in pistons, even though the drawbacks listed were enough to severely limit the specific power outputs attainable with two-stroke engines for a long time.
Aluminum-based piston alloys improved slowly over the years, with the addition of small percentages of, say, copper, to improve their hot-strength, but it was not until means were found to add considerable amounts of silicon that large improvements were made. Today, the best piston alloys contain between 15- and 25-percent silicon, and this addition has all but transformed the “aluminum” piston. Admixtures of silicon in excess of 15-percent not only drastically reduce aluminum's expansion rate, they also affect a proportionate increase in hot-strength and improve the piston's wear-resistant properties. In all of these respects the improvement is large enough to almost exactly equal the percentage gains in horsepower during the years in which aluminum-silicon alloys have been in use. I am inclined to think that most of what we consider to be “modern” improvements in two-stroke engine design – with particular reference to expansion-chamber type exhaust systems -might have been applied as much as fifty years ago had good pistons been available. There was little point in such development work without the aluminum-silicon piston; aluminum or aluminum-copper pistons would melt at specific power outputs well below what we now consider only average.
With all that, high silicon-content piston alloys still are not universally employed. As it happens, such alloys do have their disadvantage, which is that they are difficult to manufacture. Just casting pistons of aluminum-silicon alloy is a task for specialists using specialized equipment; machining the raw castings into finished pistons is an even more formidable task. You may encounter this last difficulty if you have occasion to modify a cylinder cast from the material in question - and you will find that it blunts cutting tools of any kind with remarkable rapidity. For you, that will be an inconvenience; for the mass-producer of pistons it is a disaster, as the need for frequent re-sharpening of tool bits entails losing output from his machinery while such repairs are made, and it means the expense of the man-hours required for the repairs. Thus, the manufacturer has every reason to restrict the silicon content of the piston alloys he uses to the minimum required by the use to which his engines will be put, which is the reason why Yamaha, for example, uses different alloys for touring and racing pistons.
In point of fact, the Japanese seem to manage high silicon-content pistons better than anyone else, which may well account for their notable superiority in coaxing power from two-stroke motorcycle engines. All of the major Japanese manufacturers employ piston alloys in their touring engines having percentages of silicon high enough to be considered “racing only” in much of the rest of the world. And, sad to say, many of the “racing” pistons being offered by speed equipment manufacturers are inferior in this regard to the ordinary off-the-shelf parts you'll find at your local dealer in Japanese motorcycles. For that reason, I am inclined to use either stock or “GYT-kit” pistons when I am working with engines carrying a “made in Japan” label, rather than waste my money on a specialty replacement. There are, of course, exceptions to this rule, which evolve principally around ring widths, and I will deal with that in due course.
Unless you happen to be a piston manufacturer, there isn't much you can do about piston alloys, beyond seeking out pistons having a high silicon content. Neither is there anything you can do about piston shape - which is most unfortunate, because a piston is  not, as it first appears, simply cylindrical. Even with the use of aluminum-silicon alloys, pistons do expand as they are heated, and they do not expand at all evenly. The greatest increase in diameter will occur up at the crown, because that is both the area of maximum mass and highest temperature. So there must be more clearance, measured cold, up at the piston's crown than is required down around the lower skirt. In fact, clearances vary continuously from the piston's crown to the bottom of its skirt -and from side to side, as the piston is elliptical rather than round. Someday, someone may be able, with the help of a computer, to actually calculate all the clearances and ellipse ratios involved; for the present they are decided in a process of trial-and-error by even the most experienced of manufacturers.
not, as it first appears, simply cylindrical. Even with the use of aluminum-silicon alloys, pistons do expand as they are heated, and they do not expand at all evenly. The greatest increase in diameter will occur up at the crown, because that is both the area of maximum mass and highest temperature. So there must be more clearance, measured cold, up at the piston's crown than is required down around the lower skirt. In fact, clearances vary continuously from the piston's crown to the bottom of its skirt -and from side to side, as the piston is elliptical rather than round. Someday, someone may be able, with the help of a computer, to actually calculate all the clearances and ellipse ratios involved; for the present they are decided in a process of trial-and-error by even the most experienced of manufacturers.
Presumably, you will not have the facilities to alter whatever shape your engine's piston(s) may have, but you can vary running clearances by changing cylinder bore diameter. The problem here is one of “How much?” and I regret to say that it is a problem for which there is no convenient solution. Clearances, measured at the piston's maximum diameter, across its thrust faces, may vary from about 0.002 to as much as 0.007-inch, depending on: the shape and composition of the piston itself; the absolute cylinder bore diameter; the material from which the cylinder is made, as well as its configuration; and the thermal loadings to which the piston will be subjected - which will themselves vary according to gas pressure, fuel mixture, cylinder configuration and the vehicle's rate of motion. Many people have expressed great faith in rules relating clearance to cylinder bore diameter; I have not found the choice to be that simple. If there is a rule, it would be that you can add perhaps 0.0005- to 0.001-inch to the clearance recommended by your engine's maker, but even this is a gross over-simplification and I mention it only because it is somewhat better to have too much clearance than too little. In the former, the excessive clearance adversely influences heat transfer from the piston to the relatively cooler cylinder walls and may lead to any of the several unpleasantries associated with overheating the piston, which range from a tendency for oil to become carbonized in the ring grooves, to the appearance of a large hole in the piston crown. Too little clearance will reveal itself in the form of scuffing, or outright seizure - unless the piston is only marginally too tight, in which case the only symptom of distress will be a power loss in the order of 2- to 3-percent.
Often, in modified engines, you will find that the straightforward increase in overall piston clearance by slightly enlarging the cylinder bore is not a complete answer. If the manufacturer has done his work properly, his pistons will, as they expand with temperature, assume a round shape when the engine is hot. Your problem will be that with the modifications you have made, more heat will be forced into the piston's crown, raising its temperature above the level anticipated by the manufacturer, which results in a completely different set of temperature gradients down the length of the piston. Specifically, while the whole piston will assume a diameter slightly larger than that planned for by its maker, the area around the crown will “grow” more than the rest. It will thus be impossible to correct for the altered conditions simply by honing the cylinder bore larger, for if you enlarge the bore enough to provide running clearance for the top of the piston, its skirt will be given too much clearance (leading to rocking, and trouble with the rings). In such cases, which are not the exception, but the rule, the solution is to machine what is called a “clearance band” around the top of the piston. Usually, this band will extend down from the crown to a point about 0.125-inch below the ring groove, or grooves, and the piston's diameter reduced by perhaps 0.002-inch over the entire band's width. Although the clearance band is not a particularly clean solution to the piston-expansion problem, it is one that can be applied by anyone with access to a lathe, and it has one advantage over the generally more desirable “pure” contouring of the piston: if a piston with a clearance band seizes partially, aluminum will not be smeared above and below the ring groove - an event which will lock the ring in its groove and upset its ability to seal against gas pressure, In practical terms, this means that the  clearance-banded piston will absorb a lot of punishment before it is damaged sufficiently to cause retirement from a race.
clearance-banded piston will absorb a lot of punishment before it is damaged sufficiently to cause retirement from a race.
Excessive deep clearance bands must be avoided, for they expose the sealing ring to too much heat, and heat has a devastating effect on the service life of a piston ring. But for these effects, there would be every reason to locate the ring as close to the piston crown as is mechanically possible, because we would then obtain the cleanest opening and closing of the ports; with the ring in its usual position, about 0.200-inch below the piston crown, there is a tendency for gases to leak down the side of the piston, and the port-opening process thus becomes more gradual than is desirable. The effect is slight, but it is there, and for that reason ring location always is a matter of juggling the conflicting requirements of keeping the ring cool, and obtaining sharp, clean port-opening characteristics. And in most instances, the balance of this compromise will be in favor of the former, for an overheated ring quickly fails. The cause of this failure is twofold: first, excessively high temperatures effectively anneal the ring, and it loses its radial tension; second, an overheated ring warps like a potato chip, and no longer maintains close contact with the bottom of its groove. In both of these cases, the ring's ability to seal is reduced, which allows fire to start leaking down past the ring, and that further raises its temperature -starting a cycle that soon results in outright ring failure.
The single exception to the unpleasantness just described is the L-shaped “Dykes” ring, which also is excepted from the immediate effects of ring-flutter (described elsewhere). A number of engines have been fitted very successfully with Dykes rings located right at the tops of their pistons, and the dire effects of excessive heating are avoided because the Dykes ring's vertical leg has enough area in contact with the cooler cylinder wall to draw away heat faster than it can be added by the ring's contact with high-temperature gases. At least, that's the way the situation can be, if everything is right. On the other hand, it is worth remembering that many users of Dykes-pattern rings have been forced to fabricate them from stainless alloys to overcome temperature related troubles, and even then have experienced problems with oil carbonizing in the ring grooves. Probably the best thing to be said for Dykes-pattern rings from the experimenter's viewpoint is that they can be used to overcome the problem of using stock pistons at very much higher than stock crankshaft speeds. If, for example, you would like to use the stock piston, but cannot because it has been grooved for rings 2.0mm thick and you must use 1.5mm rings to avoid ring flutter, you can simply cut a new groove at the top of the piston for a Dykes ring and the problem is solved -unless you encounter some of the other difficulties just discussed.
PISTON RINGS
Of all the problems that can be experienced with a modified engine, those connected with the pistons' rings are the most insidious. Borderline sealing failures can send fire shooting down along the pistons' sides to cause seizures and/or holing of the piston crown that appear to be the result of lean mixture, excessive ignition advance or too-high compression, but are not. These failures are, I suspect, much more frequent than is commonly supposed, for the 2.0mm rings that have become almost standard will begin to flutter when piston acceleration rises above about 60,000 ft/sec2 and it is entirely too easy to exceed that limit with a modified touring engine. Therefore, I would again urge you to do your homework before starting a development program with any engine. A formula for predicting the onset of ring flutter is provided in the chapter headed, “Fundamentals”, and you may save yourself a lot of grief by determining your engine's red-line with paper and pencil instead of through experimentation. At the same time, I must caution you against simply assuming that very narrow rings are an advantage in all engines. In fact, there is no detectable power difference between the standard 2.0mm ring and the “racing” 1.0mm ring below 7000 rpm, and the wider ring has the advantage of better durability right up to the point where piston acceleration starts it fluttering. Neither is there any advantage, below 7000 rpm, in the use of single-ring pistons. Above that level the lower friction of the single-ring piston begins to make a difference, but in the lower speed ranges you may as well use two-ring pistons and take advantage of their “second line of defense” capability.
Selection of ring-type will usually have been made for you by the piston manufacturer, and my advice is that you do not try to improve upon his judgment, which will be almost impossible in any case. You cannot, obviously, re-machine a piston made for 2.0mm rings to take 1.0mm rings -unless you cut a new ring groove above the existing grooves, and that would position your ring perilously close to the piston crown and almost certainly lead to immediate ring failure. The only way around this is to fit a Dykes-pattern ring, right up at the piston crown - as was noted previously. Such modifications can be very successful, if you have the right ring for the application and cut the groove correctly for the ring, but I cannot recommend the procedure simply because there is so much room for error. In general, I think it is far better to replace the stock piston with one fitted with thinner rings - even if the replacement piston is cast of somewhat inferior material, as is often the case. After all, the best of pistons will fail if its rings are not suited to the job it is being asked to perform. On the other hand, rings of less-than-desirable material will perform very well in racing applications if replaced frequently, and if they have not been crudely finished. Much of the ring's ability to function is related to this latter aspect. The ordinary cast-iron ring is fragile, and will shatter very quickly if allowed to flutter, but it will perform entirely satisfactorily if its lower surface is smooth and true, and seals against the bottom of the ring groove. Rings made of nodular cast-iron have the same wear-resistant properties, and are vastly stronger, for which reasons this material is almost universally used. Surface coatings, ranging from chromium to Teflon, are often applied to the piston's ring's face, to improve service life and /or prevent scuffing during break-in.
Ring sticking is a problem to be faced with all high-output two-stroke engines. Carburized oil may lock the ring in its groove after a remarkably short period of running if the ring lacks sufficient vertical clearance (usually, from 0.0015- to 0.0040-inch) or if the ring is located too near the piston crown. More frequently, the problem stems from the oil being used for lubrication, and it is most unfortunate that the very oils providing the best lubrication are the ones most likely to cause ring sticking. Castor-based oils, particularly, will build up thick layers of varnish inside the ring groove, unless the oil contains a considerable percentage of detergent chemicals.
Apart from the L-section Dykes ring, most piston rings have a basically rectangular cross-section, but you will find many minor variations on this arrangement. Currently very popular is the “keystone” ring, which has a tapered section, with either the upper or lower surface, or both, sloping away from the ring's outer face. The reason for this primarily is to keep the ring and its groove scrubbed free of carbon and varnish. In four-stroke engines the rings are free to rotate, and do, and their rotation performs this scrubbing. Two-stroke engines nearly always have their rings pinned, to prevent them from rotating and the ring's ends from springing out and becoming trapped in a port. Hence, the need for some other form of scrubbing action. Seldom is the taper in a keystone-type ring more than 7-degrees, and it is all too easy to attempt installing one of them upside-down, so you should give particular attention to the ring's markings. Such markings vary in kind, but without exception they will be on the ring's upper surface.
Another point of trouble can be the ring's locating pin, and if you encounter difficulties with locating pins working loose, the source of the trouble nearly always will be in the exhaust port. The racing engine's very wide exhaust port (width representing, in extreme instances, up to 70-percent of cylinder bore diameter) leaves a lot of the ring's diameter unsupported when the piston is down in the lower half of the cylinder, which allows the ring to bulge out into the port. Making the port opening oval and chamfering its edges will prevent the ring from snagging, as these things ease the ring back into its groove as the piston sweeps back upward. However, while the ring may not snag on the 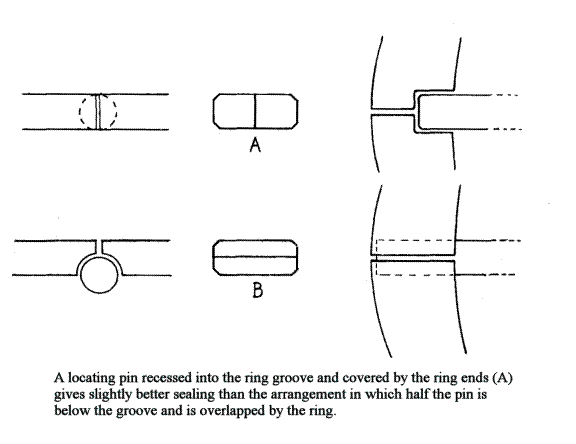 port, it does get stuffed back into its groove fairly rudely, and that may have a very bad effect on the locating pin: On most two-ring pistons, the locating pins are positioned adjacent to the areas of blind cylinder wall between the intake and transfer ports -placed about 90-degrees apart - to provide a long path for gas leakage. Thus, when the ring bulges out into the exhaust port and then is stuffed back, the end of the ring is pushed into hard contact with the pin, and after a sufficient number of hard blows (and these accumulate rapidly at, say, 10,000 rpm) the pin begins to loosen and it will gradually enlarge the hole in which it is inserted enough to work completely loose. Then the ring is free to rotate, and it quickly works its way around to catch the end in a port. At risk of seeming immodest, I will admit to having isolated this problem for Yamaha several years ago and today that firm's racing engines have pistons with locating pins positioned 180-degrees from the exhaust port. Touring engines, which have much narrower exhaust port windows and thus treat their rings more gently, usually benefit from having their two rings' end-gaps placed more nearly on opposite sides of the piston, as described before.
port, it does get stuffed back into its groove fairly rudely, and that may have a very bad effect on the locating pin: On most two-ring pistons, the locating pins are positioned adjacent to the areas of blind cylinder wall between the intake and transfer ports -placed about 90-degrees apart - to provide a long path for gas leakage. Thus, when the ring bulges out into the exhaust port and then is stuffed back, the end of the ring is pushed into hard contact with the pin, and after a sufficient number of hard blows (and these accumulate rapidly at, say, 10,000 rpm) the pin begins to loosen and it will gradually enlarge the hole in which it is inserted enough to work completely loose. Then the ring is free to rotate, and it quickly works its way around to catch the end in a port. At risk of seeming immodest, I will admit to having isolated this problem for Yamaha several years ago and today that firm's racing engines have pistons with locating pins positioned 180-degrees from the exhaust port. Touring engines, which have much narrower exhaust port windows and thus treat their rings more gently, usually benefit from having their two rings' end-gaps placed more nearly on opposite sides of the piston, as described before.
In some racing applications, the standard rings are adequate to the engine speeds anticipated, but overall performance may dictate a much wider-than stock exhaust port. Then, the “offset” ring-locating pin may prove prone to precisely the sort of loosening and subsequent failure described in the preceding paragraph, which will lead you into a piston modification that can be very tricky: installing a new locating pin in the back of the ring groove. This gets tricky because in many cases the pin will be half-in, half above, the ring groove and it is impossible to drill the hole for a new location after the groove is machined. Impossible, unless you cut a small piece of aluminum to exactly fit the ring groove, filling it flush, in which case you drill your hole half in the piston and half in the filler piece. Then you remove the filler and your hole is ready for the pin - which introduces yet another problem: what to use for a pin? Steel wire is a good choice on grounds of strength, but is likely to work loose simply because the aluminum in which it is pressed grows and contracts so much with changes in temperature. A small-diameter “split pin” (which is like a rolled tube) is a better choice, but if suitable sizes are not available, then n pin made of hard brass is at least as good.
Date: 2015-12-17; view: 4520
| <== previous page | | | next page ==> |
| Chapter Fifty-Three Letting Go: Part Three Being | | | WRISTPIN/CRANKPIN BEARINGS |