Дополнительные тексты для чтения

PROBABILITY

At the present time probability has become an acceptable part of mathematics.

In ordinary language the probability of an event means the likelihood of its occurence, and mathematical probability defines an exact measurement of this by assigning values from 0 to 1. Thus if an event is impossible, its probability equals 0; and if it is absolutely certain, its probability equals 1. If it is neither impossible nor absolutely certain, then its probability has some value between 0 and 1.

A die has 6 faces indicating the numbers from 1 to 6. The probability of throwing a 7 with one throw of 1 die equals 0 since this cannot happen. The probability that the number thrown is less than 7 equals 1, since this cannot fail (assuming ordinary conditions such that some face must come up).

Suppose an honest player throws an unloaded die. What is the probability of number 3 coming up? Since there are 6 ways the die can come up and, of these 6 ways, exactly 1 way is for number 3 to come up, we say that the probability of throwing a 3 is 1/6. Here we note that there is one way in which this event can happen and 5 ways it can fail and that all 6 ways are equally likely.

Under such circumstances probability is measured as follows: If an event can happen in h ways and can fail in f ways (all equally likely) then the probability that it will happen is given by

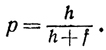
The probability that it will fail is given by

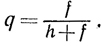
Since the event must certainly either happen or fail, the probability of its either happening or failing must equal 1. In accordance with this, we see that p+q=1. Thus, the probability of throwing a 3 was 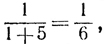so the Probability of not throwing a 3 must be .

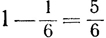Two events are mutually exclusive if they cannot both happen (under some specified conditions). Thus, when a coin is tossed once, "heads" and "tails" are mutually exclusive events.

Events which cannot affect each other in any way are called independent events. Thus the heads or tails that comes up with any particular toss of a coin is not influenced in any way by the results of previous tosses.

If the occurence of event a affects the probability of event b, then b is said to be dependent on a.

Suppose I draw out one card at random from an ordinary pack, keep this card and then draw a second card. What I draw first will affect the probabilities in regard to the second card drawn.

Date: 2015-12-11; view: 1221