Convectia libera .Ecuatii criteriale

Mecanismul transferului de cãldurã prin convecţie liberã (naturalã) este

reprezentat de mişcarea unui fluid peste o suprafaţã, mişcare produsã de diferenţa de

densitate a fluidului datoratã diferenţei de temperaturã.

In convecţia liberã, straturile limitã termic şi dinamic sunt, în principiu, de aceeaşi

grosime., deoarece gradienţii de vitezã sunt produşi de gradienţii de temperaturã. In

aceste condiţii, coeficientul de convecţie, α şi relaţiile corespunzatoare de calcul depind

direct de geometria şi orientarea suprafeţei de transfer de cãldurã.

Convecţia liberã ocupã un loc important în calculul termic al construcţiilor: calculul

pierderilor de cãldurã în mediul exterior pentru spaţiile încãlzite, calculul pãtrunderilor de

cãldurã din exterior pentru spaţiile rãcite, calculul fluxului de cãldurã pentru aparatele de

încãlzire sau rãcire etc.

In cazul conductelor care transportã fluide calde sau reci amplasate în aerul

ambiant, printr-un calcul riguros se pot obţine economii energetice importante.

La mişcarea liberã a unui fluid peste o suprafaţã, criteriul Grashof pune în

evidenţã caracterul dinamic al acesteia. Mişcarea liberã a fluidului are loc numai sub

acţiunea forţelor gravitaţionale (arhimedice) de forma (ρ.g), [N/m3].

In concluzie, pentru calculul coeficientului de convectie, α, se vor folosi ecuaţii

criteriale specifice mişcãrii fluidului.

Fenomenele de convecţie liberã se prezintã sub douã aspecte: convecţie liberã în

spaţii nelimitate (deschise) şi convecţie liberã în spaţii limitate (închise), diferenţiate prin

dimensiunile spaţiului în care are loc deplasarea fluidului în raport cu dimensiunile

principale ale curgerii.

Criteriile de similitudine caracteristice convectiei libere sunt:

-criteriul Nusselt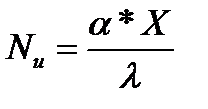

-criteriul Grashof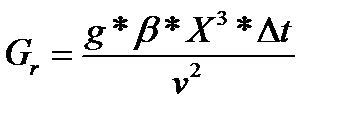

-criteriul Prandl 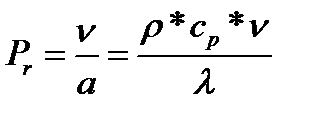(in cazul in care nu este dat tabular)

- pentru gaze, coeficientul de dilatare termicã se calculeazã cu relaţia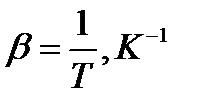

Date: 2015-12-11; view: 1314