
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Algebra and geometry
Вопрос № 1
$$1 Let  ,
,  be vectors in
be vectors in  . Find the angle between these vectors.
. Find the angle between these vectors.
$$2 0;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 2
$$1 Let  ,
,  be vectors in
be vectors in  . Find the angle between these vectors .
. Find the angle between these vectors .
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5 0;
$$6  .
.
Вопрос № 3
$$1 Let  ,
,  be vector in
be vector in  . Find the angle between these vectors.
. Find the angle between these vectors.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6 0.
Вопрос № 4
$$1 Let 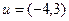 ,
, 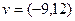 be vectors in
be vectors in  . Find the angle between these vectors
. Find the angle between these vectors
$$2 0;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 5
$$1 Let 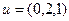 ,
,  be vectors in
be vectors in  . Find the angle between these vectors.
. Find the angle between these vectors.
$$2 0;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 6
$$1 Let  ,
, 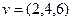 be vectors in
be vectors in  . Find the angle between these vectors.
. Find the angle between these vectors.
$$2 0;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 7
$$1 Let  ,
,  be vectors in
be vectors in  . Find the angle between these vectors..
. Find the angle between these vectors..
$$2 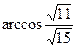 ;
;
$$3  ;
;
$$4  ;
;
$$5 0;
$$6  .
.
Вопрос № 8
$$1 Let  ,
,  be vectors in
be vectors in  . Find the angle between these vectors.
. Find the angle between these vectors.
$$2  ;
;
$$3 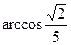 ;
;
$$4  ;
;
$$5  ;
;
$$6 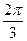 .
.
Вопрос № 9
$$1 9) Let  and
and  be vectors in
be vectors in  such that
such that  . Find
. Find  if:
if:  .
.
$$2 2;
$$3 5;
$$4 1;
$$5 15;
$$6 0.
Вопрос № 10
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find
. Find  if:
if:  .
.
$$2 -1;
$$3 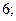
$$4 
$$5 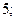
$$6 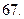
Вопрос № 11
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find
. Find  if:
if:  .
.
$$2 12;
$$3 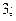
$$4 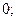
$$5 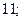
$$6 
Вопрос № 12
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find
. Find  if:
if:  .
.
$$2  ;
;
$$3 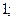
$$4 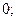
$$5 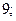
$$6 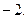
Вопрос № 13
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find
. Find  if:
if:  .
.
$$2  ;
;
$$3 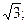
$$4 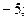
$$5 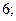
$$6 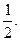
Вопрос № 14
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find the angle between
. Find the angle between 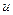 and
and  if:
if:  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 15
$$1 Let  and
and  be vectors in
be vectors in  such that
such that  . Find the angle between
. Find the angle between 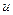 and
and  if:
if:  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 16
$$1 Determine 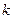 so that vectors
so that vectors 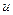 and
and  are orthogonal, where
are orthogonal, where  .
.
$$2  ;
;
$$3 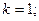
$$4 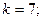
$$5 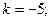
$$6 
Вопрос № 17
$$1 Determine 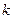 so that vectors
so that vectors 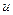 and
and  are orthogonal, where
are orthogonal, where 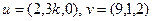 .
.
$$2 -6
$$3  ;
;
$$4 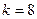 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 18
$$1 Determine 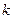 so that vectors
so that vectors 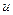 and
and  are orthogonal, where
are orthogonal, where  .
.
$$2 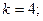
$$3 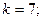
$$4 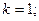
$$5 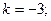
$$6 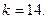
Вопрос № 19
$$1 Determine 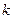 so that vectors
so that vectors 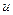 and
and  are orthogonal, where
are orthogonal, where  .
.
$$2 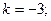
$$3 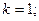
$$4 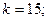
$$5 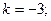
$$6 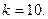
Вопрос № 20
$$1 Determine 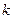 so that vectors
so that vectors 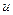 and
and  are orthogonal, where
are orthogonal, where  .
.
$$2 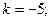
$$3 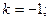
$$4 
$$5 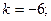
$$6 
Вопрос № 21
$$1 Find  and
and  if
if  .
.
$$2 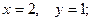
$$3 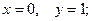
$$4 
$$5 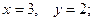
$$6 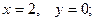
Вопрос № 22
$$1 Find  and
and  if
if  .
.
$$2 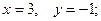
$$3 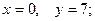
$$4 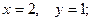
$$5 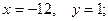
$$6 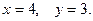
Вопрос № 23
$$1 Find  and
and  if
if  .
.
$$2 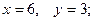
$$3 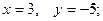
$$4 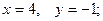
$$5 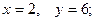
$$6 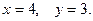
Вопрос № 24
$$1 Find  and
and  if
if  .
.
$$2 
$$3 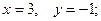
$$4 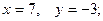
$$5 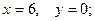
$$6 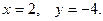
Вопрос № 25
$$1 Find  and
and  if
if  .
.
$$2 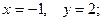
$$3 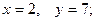
$$4 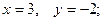
$$5 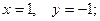
$$6 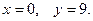
Вопрос № 26
$$1 Solve the system  .
.
$$2 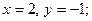
$$3 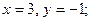
$$4 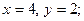
$$5 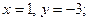
$$6 No solution.
Вопрос № 27
$$1 Solve the system  .
.
$$2 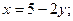
$$3 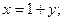
$$4 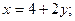
$$5 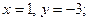
$$6 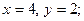
Вопрос № 28
$$1 Solve the system  .
.
$$2 No solution;
$$3 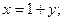
$$4 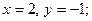
$$5 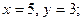
$$6 
Вопрос № 29
$$1 Solve the system  .
.
$$2 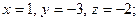
$$3 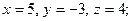
$$4 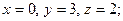
$$5 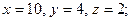
$$6 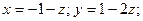
Вопрос № 30
$$1 Solve the system  .
.
$$2 No solution;
$$3 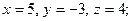
$$4 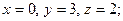
$$5 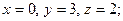
$$6 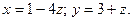
Вопрос № 31
$$1 Solve the system  .
.
$$2 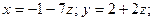
$$3 No solution;
$$4 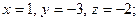
$$5 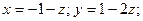
$$6 
Вопрос № 32
$$1 Determine 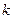 so that the system
so that the system  has the unique solution.
has the unique solution.
$$2 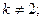
$$3 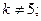
$$4 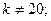
$$5 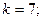
$$6 
Вопрос № 33
$$1 Determine 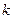 so that the system
so that the system  has the unique solution.
has the unique solution.
$$2 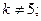
$$3 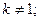
$$4 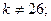
$$5 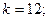
$$6 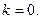
Вопрос № 34
$$1 Determine 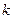 so that the system
so that the system  has the unique solution.
has the unique solution.
$$2 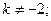
$$3 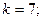
$$4 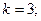
$$5 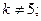
$$6 
Вопрос № 35
$$1 Determine 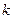 so that the system
so that the system 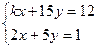 has the unique solution.
has the unique solution.
$$2 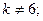
$$3 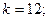
$$4 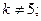
$$5 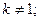
$$6 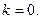
Вопрос № 36
$$1 Determine 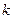 so that the system
so that the system  has the unique solution.
has the unique solution.
$$2 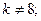
$$3 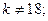
$$4 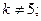
$$5 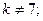
$$6 
Вопрос № 37
$$1 Determine 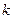 so that the system
so that the system  has more the one solution.
has more the one solution.
$$2 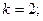
$$3 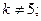
$$4 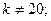
$$5 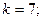
$$6 
Вопрос № 38
$$1 Determine 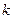 so that the system
so that the system  has more then one solution.
has more then one solution.
$$2 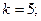
$$3 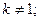
$$4 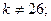
$$5 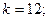
$$6 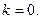
Вопрос № 39
$$1 Determine 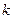 so that the system
so that the system  has more then one solution.
has more then one solution.
$$2 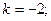
$$3 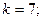
$$4 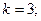
$$5 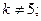
$$6 
Вопрос № 40
$$1 $$1 Determine 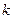 so that the system
so that the system 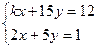 has more then one solution.
has more then one solution.
$$2 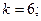
$$3 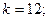
$$4 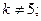
$$5 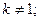
$$6 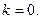
Вопрос № 41
$$1 Determine 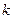 so that the system
so that the system  has more then one solution.
has more then one solution.
$$2 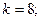
$$3 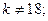
$$4 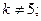
$$5 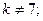
$$6 
Вопрос № 42
$$1 Let  . Find
. Find 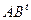 .
.
$$2 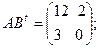
$$3 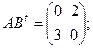
$$4 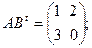
$$5 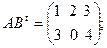
$$6 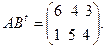
Вопрос № 43
$$1 Let  . Find
. Find 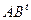 .
.
$$2 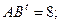
$$3 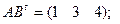
$$4 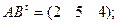
$$5 
$$6 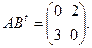
Вопрос № 44
$$1 Let  . Find
. Find 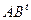 .
.
$$2 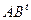 does not exist;
does not exist;
$$3 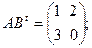
$$4 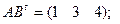
$$5 
$$6 
Вопрос № 45
$$1 Let  ,
,  . Find
. Find 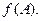
$$2 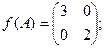
$$3 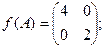
$$4 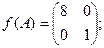
$$5 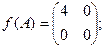
$$6 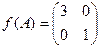 .
.
Вопрос № 46
$$1 Let  ,
,  . Find
. Find 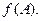
$$2 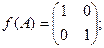
$$3  s
s
$$4 
$$5 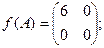
$$6  .
.
Вопрос № 47
$$1 Let  ,
,  . Find
. Find 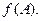
$$2 
$$3 
$$4 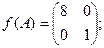
$$5 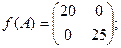
$$6 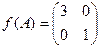 .
.
Вопрос № 48
$$1 Given  . Find a vector
. Find a vector  such that
such that  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5 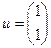 ;
;
$$6  .
.
Вопрос № 49
$$1 Given 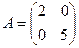 . Find a vector
. Find a vector  such that
such that  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5 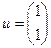 ;
;
$$6  .
.
Вопрос № 50
$$1 Given  . Find a vector
. Find a vector  such that
such that  .
.
$$2  ;
;
$$3 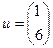 ;
;
$$4  ;
;
$$5 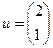 ;
;
$$6  .
.
Вопрос № 51
$$1 Write the vector  as a linear combination of the vectors
as a linear combination of the vectors  .
.
$$2 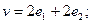
$$3 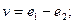
$$4 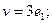
$$5 
$$6 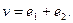
Вопрос № 52
$$1 Write the vector  as a linear combination of the vectors
as a linear combination of the vectors  .
.
$$2 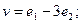
$$3 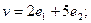
$$4 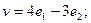
$$5 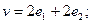
$$6 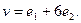
Вопрос № 53
$$1 Write the vector  as a linear combination of the vectors
as a linear combination of the vectors  .
.
$$2 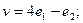
$$3 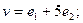
$$4 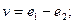
$$5 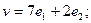
$$6 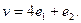
Вопрос № 54
$$1 Write the vector  as a linear combination of the vectors
as a linear combination of the vectors  .
.
$$2 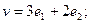
$$3 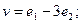
$$4 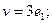
$$5 
$$6 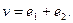
Вопрос № 55
$$1 Write 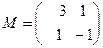 as a linear combination of matrices
as a linear combination of matrices
 .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 56
$$1 Write  as a linear combination of matrices
as a linear combination of matrices
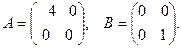
$$2 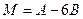 ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 57
$$1 Write  as a linear combination of matrices
as a linear combination of matrices
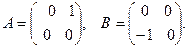
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 58
Write 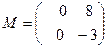 as a linear combination of matrices
as a linear combination of matrices
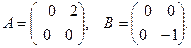
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 59
$$1 Find the rank of matrix  .
.
$$2 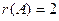 ;
;
$$3 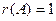 ;
;
$$4  ;
;
$$5 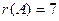 ;
;
$$6  .
.
Вопрос № 60
$$1 Find the rank of matrix  .
.
$$2 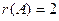 ;
;
$$3  ;
;
$$4 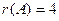
$$5 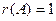
$$6 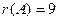
Вопрос № 61
$$1 Find the rank of matrix  .
.
$$2  ;
;
$$3 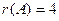 ;
;
$$4 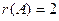 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 62
$$1 Find the rank of matrix  .
.
$$2 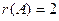 ;
;
$$3  ;
;
$$4  ;
;
$$5 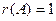
$$6  .
.
Вопрос № 63
$$1 Find the rank of matrix  .
.
$$2 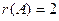 ;
;
$$3 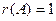 ;
;
$$4  ;
;
$$5 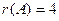 ;
;
$$6  .
.
Вопрос № 64
$$1 Find the rank of matrix 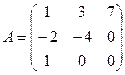 .
.
$$2  ;
;
$$3 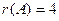 ;
;
$$4 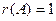 ;
;
$$5  ;
;
$$6 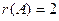 .
.
Вопрос № 65
$$1 Find the rank of matrix  .
.
$$2 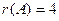 ;
;
$$3 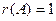 ;
;
$$4 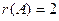 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 66
$$1 Find the rank of matrix  .
.
$$2 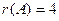 ;
;
$$3  ;
;
$$4  ;
;
$$5  ;
;
$$6 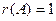 .
.
Вопрос № 67
$$1 Find a dimension of the solution space  of the homogeneous system
of the homogeneous system
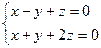 .
.
$$2 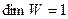
$$3 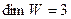 ;
;
$$4 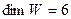 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 68
$$1 Find a dimension of the solution space  of the homogeneous system
of the homogeneous system
 .
.
$$2 
$$3 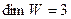 ;
;
$$4 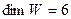 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 69
$$1 $$1 Find a dimension of the solution space  of the homogeneous system
of the homogeneous system
 .
.
$$2 
$$3 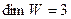 ;
;
$$4  ;
;
$$5 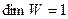 ;
;
$$6  .
.
$$1 Find a dimension of the solution space  of the homogeneous system
of the homogeneous system
 .
.
$$2 
$$3  ;
;
$$4 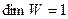 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 70
$$1 Find a dimension of the solution space  of the homogeneous system
of the homogeneous system
 .
.
$$2 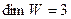
$$3  ;
;
$$4 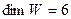 ;
;
$$5  ;
;
$$6  .
.
Вопрос № 71
$$1 Find a dimension of the subspace  of
of  generated by vectors
generated by vectors  .
.
$$2  ;
;
$$3 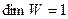 ;
;
$$4  ;
;
$$5 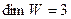 ;
;
$$6  .
.
Вопрос № 72
$$1 Find a dimension of the subspace  of
of  generated by vectors
generated by vectors  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5 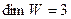 ;
;
$$6 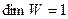 .
.
Вопрос № 73
$$1 Find a dimension of the subspace  of
of  generated by vectors
generated by vectors  .
.
$$2 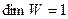 ;
;
$$3  ;
;
$$4  ;
;
$$5 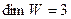 ;
;
$$6  .
.
Вопрос № 74
$$1 Find a dimension of the subspace  of
of  generated by vectors
generated by vectors 
 .
.
$$2 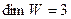 ;
;
$$3 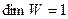 ;
;
$$4  ;
;
$$5  ;
;
$$6  .
.
Вопрос № 75
$$1 Find a dimension of the subspace  of
of  generated by vectors
generated by vectors  ,
,  .
.
$$2  ;
;
$$3  ;
;
$$4 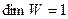 ;
;
$$5 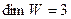 ;
;
$$6 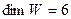 .
.
Вопрос № 76
$$1 Let  be linear operators on
be linear operators on  defined by
defined by  . Find
. Find  .
.
$$2  ;
;
$$3  ;
;
$$4  ;
;
$$5 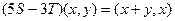 ;
;
$$6  .
.
Вопрос № 77
$$1 Let  be linear operators on
be linear operators on  defined by
defined by  . Find
. Find 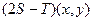
Date: 2015-12-11; view: 1351
| <== previous page | | | next page ==> |
| | | Die Teilgebiete der Algebra |