
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Then the probability that P(X < 2.0) is equal to
Compute the expectation of X.
o 7/72
o 1/8
· 5/6
o 4/3
o 23/12
58. A fair coin is thrown in the air four times. If the coin lands with the head up on the first three tosses, what is the probability that the coin will land with the head up on the fourth toss?
o 0
o 1/16
o 1/8
· 1/2
o 1/4
59. A movie theater sells 3 sizes of popcorn (small, medium, and large) with 3 choices of toppings (no butter, butter, extra butter). How many possible ways can a bag of popcorn be purchased?
o 1
o 3
· 9
o 27
o 62
60. A random variable Y has the following distribution:
Y | -1 0 1 2
P(Y)| 3C 2C 0.4 0.1 The value of the constant C is:
· 0.1
o 0.15
o 0.20
o 0.25
o 0.75
61. A random variable X has a probability distribution as follows:
X | 0 1 2 3
P(X) | 2k 3k 13k 2k
Then the probability that P(X < 2.0) is equal to
o 0.90
· 0.25
o 0.65
o 0.15
o 1
62. Which one of these variables is a continuous random variable?
· The time it takes a randomly selected student to complete an exam.
o The number of tattoos a randomly selected person has.
o The number of women taller than 68 inches in a random sample of 5 women.
o The number of correct guesses on a multiple choice test.
o The number of 1’s in N rolls of a fair die
63. Heights of college women have a distribution that can be approximated by a normal curve with a mean of 65 inches and a standard deviation equal to 3 inches. About what proportion of college women are between 65 and 67 inches tall?
o 0.75
o 0.5
· 0.25
o 0.17
o 0.85
64. The probability is p = 0.80 that a patient with a certain disease will be successfully treated with a new medical treatment. Suppose that the treatment is used on 40 patients. What is the "expected value" of the number of patients who are successfully treated?
o 40
o 20
o 8
· 32
o 124
65. A medical treatment has a success rate of 0.8. Two patients will be treated with this treatment. Assuming the results are independent for the two patients, what is the probability that neither one of them will be successfully cured?
o 0.5
o 0.36
o 0.2
· 0.04
o 0.4
66. A set of possible values that a random variable can assume and their associated probabilities of occurrence are referred to as ...
· Probability distribution
o The expected value
o The standard deviation
o Coefficient of variation
o Correlation
67. Given a normal distribution with µ=100 and σ=10, what is the probability that X>75?
· 0.99
o 0.25
o 0.49
o 0.45
o 0
68. Which of the following is not a property of a binomial experiment?
o the experiment consists of a sequence of n identical trials
o each outcome can be referred to as a success or a failure
· the probabilities of the two outcomes can change from one trial to the next
o the trials are independent
o binomial random variable can be approximated by the Poisson
69. Which of the following random variables would you expect to be discrete?
o The weights of mechanically produced items
· The number of children at a birthday party
o The lifetimes of electronic devices
o The length of time between emergency arrivals at a hospital
o The times, in seconds, for a 100m sprint
70. Two events each have probability 0.2 of occurring and are independent. The probability that neither occur is
· 0.64
o 0.04
o 0.2
o 0.4
o none of the given answers
71. A smoke-detector system consists of two parts A and B. If smoke occurs then the item A detects it with probability 0.95, the item B detects it with probability 0.98 whereas both of them detect it with probability 0.94. What is the probability that the smoke will not be detected?
· 0.01
o 0.99
o 0.04
o 0.96
o None of the given answers
72. A class consists of 490 female and 510 male students. The students are divided according to their marks Passed and Did not pass
| Passed | Did not pass | |
| Female | ||
| Male |
If one person is selected randomly, what is the probability that it did not pass given that it is male.
o 0.066
o 0.124
o 0.414
o 0.812
· 0.196
73. A company which produces a particular drug has two factories, A and B. 30% of the drug are made in factory A, 70% in factory B. Suppose that 95% of the drugs produced by the factory A meet specifications while only 75% of the drugs produced by the factory B meet specifications. If I buy the drug, what is the probability that it meets specifications?
o 0.95
· 0.81
o 0.75
o 0.7
o 0.995
74. Twelve items are independently sampled from a production line. If the probability any given item is defective is 0.1, the probability of at most two defectives in the sample is closest to …
o 0.3874
o 0.9872
o 0.7361
· 0.8891
o None of the shown answers
75. A student can solve 6 from a list of 10 problems. For an exam 8 questions are selected at random from the list. What is the probability that the student will solve exactly five problems?
o 0.282
o 0.02
o 0.376
· 0.133
o None of the shown answers
76. Suppose that 10% of people are left handed. If 8 people are selected at random, what is the probability that exactly 2 of them are left handed?
o 0.0331
o 0.0053
· 0.1488
o 0.0100
o 0.2976
77. Suppose a computer chip manufacturer rejects 15% of the chips produced because they fail presale testing. If you test 4 chips, what is the probability that not all of the chips fail?
· 0.9995
o 5.06 × 10-4
o 0.15
o 0.6
o 0.5220
78. Which of these has a Geometric model?
o the number of aces in a five-card Poker hand
o the number of people we survey until we find two people who have taken Statistics
o the number of people in a class of 25 who have taken Statistics
· the number of people we survey until we find someone who has taken Statistics
o the number of sodas students drink per day
79. In a certain town, 50% of the households own a cellular phone, 40% own a pager, and 20% own both a cellular phone and a pager. The proportion of households that own neither a cellular phone nor a pager is
o 90%
o 70%
o 10%
· 30%.
o 25%
80. Four persons are to be selected from a group of 12 people, 7 of whom are women. What is the probability that the first and third selected are women?
· 0.3182
o 0.5817
o 0.78
o 0.916
o 0.1211
81. Twenty percent of the paintings in a gallery are not originals. A collector buys a painting. He has probability 0.10 of buying a fake for an original but never rejects an original as a fake, What is the (conditional) probability the painting he purchases is an original?
o 1/41
· 40/41
o 80/41
o 1
o 40/100
82. Suppose that the random variable T has the following probability distribution:
t | 0 1 2 --------------------------- P(T = t) | .5 .3 .2
Find  .
.
o 0.8
· 0.5
o 0.3
o 0.2
o 0.1
83. A probability function is a rule of correspondence or equation that:
o Finds the mean value of the random variable.
o Assigns values of x to the events of a probability experiment.
· Assigns probablities to the various values of x.
o Defines the variability in the experiment.
o None of the given answers is correct.
84. Which of the following is an example of a discrete random variable?
o The distance you can drive in a car with a full tank of gas.
o The weight of a package at the post office.
o The amount of rain that falls over a 24-hour period.
· The number of cows on a cattle ranch.
o The time that a train arrives at a specified stop.
85. Which of the following is the appropriate definition for the union of two events A and B?
o The set of all possible outcomes.
o The set of all basic outcomes contained within both A and B.
· The set of all basic outcomes in either A or B, or both.
o None of the given answers
o The set of all basic outcomes that are not in A and B.
86. Johnson taught a music class for 25 students under the age of ten. He randomly chose one of them. What was the probability that the student was under twelve?
· 1
o 0.5
o 1/25
o 0
o 0.25
87. The compact disk Jane bought had 12 songs. The first four were rock music. Tracks number 5 through 12 were ballads. She selected the random function in her CD Player. What is the probability of first listening to a ballad?
o 1/3
· 2/3
o 1/2
o 1/6
o 1/12
88. Two fair dice, one red and one blue, each have numbers 1-6. If a roll of the two dice totals 6, what is the probability that the red die is showing a 5?
o 1/6
· 1/5
o 1/3
o 5/6
o 1/18
89. A regular deck of 52 cards contains 4 different suits (Spades, Hearts, Diamonds, and Clubs) that each have 13 cards. If you randomly choose two cards from the deck, what is the probability that both cards will all be hearts?
o 4/17
· 1/17
o 2/17
o 1/4
o 4/17
o 33/68
90. What is the probability of drawing a diamond from a standard deck of 52 cards?
o 1/52
o 13/39
o 1/13
· 1/4
o 1/2
91. One card is randomly selected from a shuffled deck of 52 cards and then a die is rolled. Find the probability of obtaining an Ace and rolling an odd number.
o 1/104
o 7/13
o 1/39
· 1/26
o 1/36
92. The probability that a particular machine breaks down on any day is 0.2 and is independent of the breakdowns on any other day. The machine can break down only once per day. Calculate the probability that the machine breaks down two or more times in ten days.
o 0.0175
o 0.0400
o 0.2684
· 0.6242
o 0.9596
93. Let A, B and C be independent events such that P(A) = 0.5, P(B) = 0.6 and P(C) = 0.1. Calculate 
o 0.69
o 0.71
· 0.73
o 0.98
o 1
94. The pdf of a random variable X is given by  .
.
What are the values of µ and σ?
o 
o 
· 
o 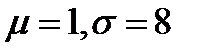
o 
95. What quantity is given by the formula  ?
?
o Covariance of the random variables X and Y
· Correlation coefficient
o Coefficient of symmetry
o Conditional expectation
o None of the given answers is correct
96. In the first step, Joe draws a hand of 5 cards from a deck of 52 cards. What is the probability that Joe has exactly one ace?
· 0.2995
o 0.699
o 0.23336
o 1/4
o 0.4999
97. The number of clients arriving each hour at a given branch of a bank asking for a given service follows a Poisson distribution with parameter λ=3. It is assumed that arrivals at different hours are independent from each other. The probability that in a given hour at most 2 clients arrive at this specific branch of the bank is:
o 0.64726
o 0.81521
· 0.42319
o 0.18478
o 0.08391
98. Table shows the cumulative distribution function of a random variable X. Determine  .
.
| X | ||||
| F(X) | 1/8 | 3/8 | 3/4 |
o 1/8
· 7/8
o 1/2
o 3/4
o 1/3
99. Table shows the cumulative distribution function of a random variable X. Determine  .
.
| X | ||||
| F(X) | 1/8 | 3/8 | 3/4 |
o 1/8
o 1
o 1/2
o 3/4
· 0
100. Which of the following statements is always true for A and  ?
?
o P(AAc)=1
o P(Ac)=P(A)
o P(A+Ac)=0
· P(AAc)=0
o None of the given statements is true
101. Consider the universal set U and two events A and B such that  and
and  . We know that P(A)=1/3. Find P(B).
. We know that P(A)=1/3. Find P(B).
· 2/3
o 1/3
o 4/9
o Cannot be determined
o 1
102. A box contains 5 red and 4 white marbles. Two marbles are drawn successively from the box without replacement and it is noted that the second one is white. What is the probability that the first is also white?
o 1/3
· 3/8
o 5/8
o 1/8
o 1
103. If P(A)=1/2 and P(B)=1/2 then 
o 1/4, always
· 1/4, if A and B are independent
o 1/2, always
o 1/2, if A and B are independent
o None of the given answers
104. Suppose that P(A|B)=3/5, P(B)=2/7, and P(A)=1/4. Determine P(B|A).
o 24/75
· 24/35
o 6/35
o 12/75
o None of the given answers
105. A class contains 8 boys and 7 girls. The teacher selects 3 of the children at random and without replacement. Calculate the probability that the number of boys selected exceeds the number of girls selected.
o 512/3375
· 28/65
o 8/15
o 1856/3375
o 36/65
106. If the variance of a random variable X is equal to 3, then Var(3X) is :
o 12
o 6
o 3
· 27
o 9
107. Let X and Y be continuous random variables with joint cumulative distribution function  for
for  and
and  . Find P(X>2).
. Find P(X>2).
o 3/125
o 11/50
· 12/25
o 
o 
108. Indicate the correct statement related to Poisson random variable  .
.
·  ,
, 
o  ,
, 
o  ,
, 
o  ,
,  is const
is const
o None of the given answers is correct
109. Let X be a continuous random variable with PDF f(x) = cx (0 ≤ x ≤ 1), where c is a constant. Find the value of constant c.
o 1
· 2
o 1/2
o 3/2
o 4
110. We are given the pmf of two random variables X and Y shown in the tables below.
| Х | У | ||||||
| px | 0,4 | 0,6 | py | 0,2 | 0,8 |
Find E[X+Y].
· 5,8
o 2,2
o 2
o 8,8
o 10
111. The pdf of a random variable X is given by  . Calculate the parameter
. Calculate the parameter  .
.
o 0
· 4
o 1,5
o 2
o 3,5
112. Four persons are to be selected from a group of 12 people, 7 of whom are women. What is the probability that three of those selected are women?
· 0.35
o 0.65
o 0.45
o 0.25
o 0.1211
113. Suppose that the random variable T has the following probability distribution:
t | 0 1 2 --------------------------- P(T = t) | .5 .3 .2 Find  .
.
· 0.8
o 0.5
o 0.3
o 0.2
o 0.1
114. Suppose that the random variable T has the following probability distribution:
t | 0 1 2 --------------------------- P(T = t) | .5 .3 .2 Compute the mean of the random variable T.
o 0.8
o 0.5
· 0.7
o 0.1
o 1
115. Three dice are rolled. What is the probability that the points appeared are distinct.
o 1
· 5/9
o 2
o 1/3
o 1/2
116. Probability density function of the normal random variable X is given by 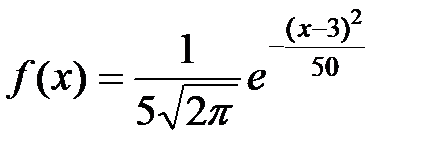 . What is the standard deviation?
. What is the standard deviation?
· 5
o 3
o 25
o 50
o 9
117. The event A occurs in each of the independent trials with probability p. Find probability that event A occurs at least once in the 5 trials.
o 
· 
o 
o 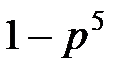
o None of the given answers is correct
118. The cdf of a random variable X is given by 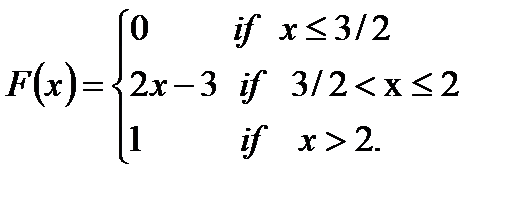 Find the probability P(1.7<X<1.9).
Find the probability P(1.7<X<1.9).
o 0,16
o 0,8
o 1
· 0,4
o 0.6
119. In each of the 20 independent trials the probability of success is 0.2. Find the variance of the number of successes in these trials.
o 0
o 1
o 10
· 3.2
o 0.32
120. A coin tossed twice. What is the probability that head appears in the both tosses.
o 1/2
· 1/4
o 0
o 4:1
o 1
121. Continuous random variable X is normally distributed with mean=1 and variance=4. Find P(4≤x≤6).
· 0,0606
o 0,202
o 0,0305
o 0,0484
o 0,0822
122. Random variable X is uniformly distributed on the interval [-2, 2]. Indicate the right values for E[X] and Var(X).
o E[X]=0 and Var(X)=4
· E[X]=0 and Var(X)=1.33
o E[X]=0.5 and Var(X)=1.33
o E[X]=0 and Var(X)=0
o No right answer
123. Expectation and standard deviation of the normally distributed random variable X are respectively equal to 15 and 5. What is the probability that in the result of an experiment X takes on the value in interval (5, 20)?
o F(20) – F(5)
o F(5) + F(10)
o F(1) – F(0)
o F(20) + F(5)
· F(1) + F(2)-1
o F(2) – F(1)
124. Normally distributed random variable X is given by density  . Findthemean.
. Findthemean.
o -1/2
o 1/2
o 1/4
· 0
o 1
125. Indicate the density function of the normally distributed random variable X when mean=2 and variance=9.
o 
o 
· 
o 
o 
126. Indicate the PDF for standard normal random variable.
o  ,
, 
o 
o  ,
, 
· 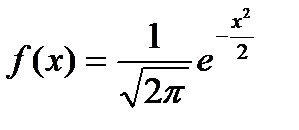
o 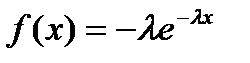 ,
, 
127. Random variable X is uniformly distributed in interval [0, 3]. What is the variance of X?
· 0.75
o 1.5
o 3
o 0.25
o 1
128. Random variable X is uniformly distributed in interval [0, 15]. What is the expectation of X?
o 15
o 3.75
· 7.5
o 30
o 0
129. Random variable X is uniformly distributed in interval [-2, 1]. What is the distribution of the random variable Y=2X+2?
o Y is normally distributed in the interval [-4, 2]
· Y is uniformly distributed in the interval [-2, 4]
o Y is normally distributed in the interval [-2, 4]
o Y is exponentially distributed in the interval [-4, 2]
o Y has other type of distribution
130. Random variable X is uniformly distributed in interval [-11, 26]. What is the probability P(X> - 4)?
o 29/38
o 29/37
· 30/37
o 15/19
o 0
131. Random variable X is uniformly distributed in interval [1, 3]. What is the distribution of the random variable Y=3X+1?
o Y is normally distributed in the interval [3, 9]
· Y is uniformly distributed in the interval [4, 10]
o Y is normally distributed in the interval [4, 10]
o Y is exponentially distributed in the interval [4, 10]
o Y has other type of distribution
132. Random variable X is uniformly distributed in interval [-11, 20]. What is the probability P(X ≤ 0) ?
o 11/32
o 5/16
o 10/31
· 11/31
o 0
133. Random variable X is given by density function f(x) in the interval (0, 1) and otherwise is 0. What is the expectation of X?
o 
o 
· 
o 
o E[X]=0
134. Random variable X is given by density function f(x) = x/2 in the interval (0, 2) and otherwise is 0. What is the expectation of X?
o 1/2
o 1
· 4/3
o 2/3
o 0
135. Random variable X is given by density function f(x) = 2x in the interval (0, 1) and otherwise is 0. What is the expectation of X?
o 1/2
o 1
o 4/3
· 2/3
o 0
136. Random variable X is given by density function f(x) = 2x in the interval (0, 1) and otherwise is 0. What is the probability P(0 < X < 1/2) ?
o 1/2
· 1/4
o 0
o 1/8
o 0
o None of these
137. Indicate the function that can be CDF of some random variable.
o 
o 
· 
o 
o None of these
138. Indicate the function that can be PDF of some random variable.
· 
o 
o 
o 
o 
139. Continuous random variable X has the following CDF:
 . What is the PDF of X in the interval 1<X≤2?
. What is the PDF of X in the interval 1<X≤2?
· 1/2
o 0
o 1
o X2/4
o x
140. Continuous random variable X is given in the interval [0, 100]. What is the probability P(X=50)?
· 0
o 1
o 0.5
o 0.75
o 0.25
141. CDF of discrete random variable X is given by
 What is the probability P{1.3<X≤2.3}?
What is the probability P{1.3<X≤2.3}?
o 0.8
· 0.2
o 0
o 0.6
o 0.4
142. PMF of discrete random variable is given by
| Х | |||
| Р | 0,1 | 0,5 | 0,4 |
Find the value of CDF of X in the interval (2, 4].
o 0.4
o 0.5
o 0.2
· 0.6
o 1
143. PMF of discrete random variable is given by
| Х | |||
| Р | 0,3 | 0,1 | 0,6 |
Find F(2).
· 0.4
o 0.6
o 0.3
o 0.7
o 0.1
144. PMF of discrete random variable X is given by
| Х | -1 | |
| Р | 0,4 | 0,6 |
Find standard deviation of X.
o 15.4
o 8.64
o 2.6
· 2.9393
o 3.3333
145. PMF of discrete random variable X is given by
| Х | -1 | |
| Р | 0,4 | 0,6 |
Find variance of X.
o 15.4
· 8.64
o 2.6
o 2.93
o 3.33
146. PMF of discrete random variable X is given by
| Х | 
| ||
| Р | 0,6 | 0,1 | 0,3 |
If E[X]=3.5 then find the value of x3.
· 10
o 6
o 8
o 12
o 24
147. Probability of success in each of 100 independent trials is constant and equals to 0.8. What is the probability that the number of successes is between 60 and 88?
o 
· 
o 
o 
o 
148. A man is made 10 shots on the target. Assume that the probability of hitting the target in one shot is 0,7. What is the most probable number of hits?
o 8
· 7
o 6
o 5
o 9
149. Consider two boxes, one containing 4 white and 6 black balls and the other - 8 white and 2 black balls. A box is selected at random, and a ball is drawn at random from the selected box. If the ball occurs to be white, what is the probability that the first box was selected?
o 0.4
o 0.6
o 0.8
· 1/3
o 2/3
150. Each of two boxes contains 6 white and 4 black balls. A ball is drawn from 1st box and it is replaced to the 2nd box. Then a ball is drawn from the 2nd box. What is the probability that this ball occurs to be white?
o 0.3
o 0.4
o 0.5
· 0.6
o 0.8
151. Consider two boxes, one containing 3 white and 7 black balls and the other – 1 white and 9 black balls. A box is selected at random, and a ball is drawn at random from the selected box. What is the probability that the ball selected is black?
· 0.8
o 0.2
o 0.4
o 1.6
o 0.9
152. Urn I contains 4 black and 6 white balls, whereas urn II contains 3 white and 7 black balls. An urn is selected at random and a ball is drawn at random from the selected urn. What is the probability that the ball is white?
· 0.45
o 0.15
o 0.4
o 0.9
o 1
153. A coin is tossed twice. Event A={ at least one Head appears}, event B={at least one Tail appears}. Find the conditional probability P(B|A).
· 2/3
o 1/3
o 1/2
o 3/4
o 0
154. A coin is tossed twice. Event A={ Head appears in the first tossing}, event B={at least one Tail appears}. Find the conditional probability P(B|A).
o 1/4
· 1/2
o 1/3
o 2/3
o 3/4
155. Probability that each shot hits a target is 0.9. Total number of shots produced to the target is 5. What is the probability that at least one shot hits the target?
o 1-0,95
o 0,95
o 1-5×0,9
· 1-0,15
o 0,15
o 1-5×0,1
156. An urn contains 1 white and 9 black balls. Three balls are drawn from the urn without replacement. What is the probability that at least one of the balls is white?
o 0.7
· 0.3
o 0.4
o 0.2
o 0.6
157. Four independent shots are made to the target. Probability of missing in the first shot is 0.5; in the second shot – 0.3; in the 3rd – 0.2; in the 4th – 0.1. What is the probability that the target is not hit.
o 1.1
o 0.03
o 0.275
· 0.003
o 1.01
158. Probability of successful result in the certain experiment is 3/4. Find the most probable number of successful trials, if their total number is 10.
o 6
o 7
· 8
o 5
o 10
159. Let E and F be two mutually exclusive events and P(E)=P(F)=1/3. The probability that none of them will occur is:
o No correct answer
· 
o 
o 
o 
160. Let E and F be two events. If 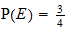 ,
,  ,
,  and
and  , then the conditional probability of E given F is:
, then the conditional probability of E given F is:
o 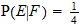
o 
· 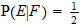
o 
o No correct answer
161. Given that Z is a standard normal random variable. What is the value of Z if the area to the left of Z is 0.9382?
o 1.8
· 1.54
o 2.1
o 1.77
o 3
162. At a university, 14% of students take math and computer classes, and 67% take math class. What is the probability that a student takes computer class given that the student takes math class?
o 0.81
· 0.21
o 0.53
o No correct answer
o 0.96
163. Let  ,
, 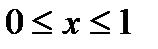 ,
,  , be the joint p.d.f. of X and Y. Find the marginal PDF of X.
, be the joint p.d.f. of X and Y. Find the marginal PDF of X.
o x
· x+1/2
o y+1/2
o x2+1
o x2+y2
164. If two random variables X and Y have the joint density function,  , find the probability P(X+Y<1).
, find the probability P(X+Y<1).
· 1/24
o 1/12
o 5/12
o 1/4
o 0.003
165. If two random variables X and Y have the joint density function,  , find the conditional PDF
, find the conditional PDF 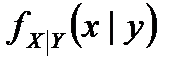 .
.
o 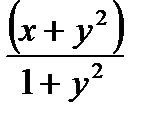
· 

o 
o 
o None of these
166. If two random variables X and Y have the joint density function,  , find the conditional PDF
, find the conditional PDF  .
.
o 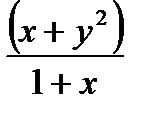
o 
· 
o 
o None of these
167. A basketball player makes 90% of her free throws. What is the probability that she will miss for the first time on the seventh shot?
o 0.0001
· 0.053
o 0.002
o 0.001
o 0.01
168. The joint distribution for two random variables X and Y is given by 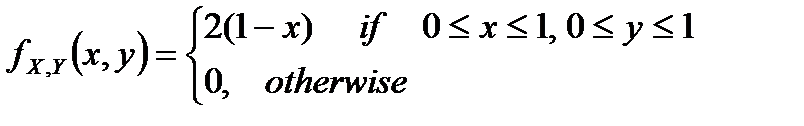 . Then find P(Y>0.5).
. Then find P(Y>0.5).
· 0.5
o 0.25
o 0.75
o 1
o 1.5
169. Let X be a continuous random variable with probability density given by  . Let Y=2X-3. Find P(Y≥4).
. Let Y=2X-3. Find P(Y≥4).
o 0.3438
· 0.53125
o 0.0625
o 0.1563
o 0
170. Random variable X has the following PDF 
Find  .
.
o 0.31
o 0.428
· 0.512
o 0
o 0.78
171. Random variable X has the following PDF 
Find E[X].
· 0
o 1
o 2
o 3
o 4
172. Random variable X has the following PDF 
Find Var[X].
o 0
o 1
· 0.6
o 0.8
o 0.4
173. Random variable X has the following PDF 
Find  .
.
o 4
· 0
o 2
o 1
o -2
174. The joint distribution for two random variables X and Y is given by  . Find the marginal density function for X.
. Find the marginal density function for X.
o 6y
o 6y2
o 6x2
· 3x2
o 3x3
175. The joint distribution for two random variables X and Y is given by  . Find the marginal density function for Y.
. Find the marginal density function for Y.
o 3x2
o 6y
· 2y
o 2y2-1
o y+6
176. The joint distribution for two random variables X and Y is given by  . Find the E[X].
. Find the E[X].
o 0.25
· 0.75
o 0.5
o 0.95
o None of these
177. The joint distribution for two random variables X and Y is given by  . Find the E[Y].
. Find the E[Y].
o 1
· 2/3
o 1/3
o 0.5
o 0.25
178. Assume that Z is standard normal random variable. What is the probability P(|Z|>2.53)?
o 0.9943
· 0.0114
o 0.0057
o 0.9886
o None of these
179. If Z is normal random variable with parameters µ=0, σ2=1 then the value of c such that P(|Z|<c)=0.7994 is
· 1.28
o 0.84
o 1.65
o 2.33
o None of these
180. The random variable X has the continuous CDF
 . Find P(2≤X≤4).
. Find P(2≤X≤4).
o 16/9
o 4/3
o 4/9
· 5/9
o 2/3
181. Let X be the random variable for the life in hours for a certain electronic device. The probability density function is
 . Find the expected life for a component.
. Find the expected life for a component.
· 2000 hours
o 1000 hours
o 100 hours
o 200 hours
o None of these
182. The joint distribution for two random variables X and Y is given by  . Find E[X-Y].
. Find E[X-Y].
· 0
o 7/6
o 2/3
o 1/6
o None of these
183. The joint distribution for two random variables X and Y is given by  . Find E[X+Y].
. Find E[X+Y].
o 1/6
o 6/7
· 7/6
o 5/6
o 0
184. The joint density function for the random variables X and Y is given by 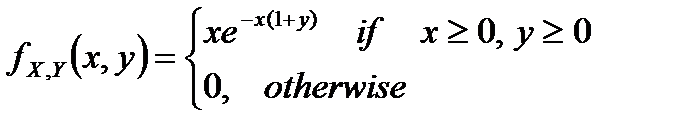 . Find E[X].
. Find E[X].
o 0
· 1
o 1.4142
o 2
o None of these
185. A box contains 15 balls, 10 of which are black. If 3 balls are drawn randomly from the box, what is the probability that all of them are black?
· 0.26
o 0.52
o 0.1
o None of these
o 0.36
186. The Cov(aX,bY) is equal to
o 
o 
· 
o 
o 
187. If A and B are two mutually exclusive events with P(A) = 0.15 and P(B) = 0.4, find the probability P(A and Bc) (i.e. probability of A and B complement).
o 0.4
· 0.15
o 0.85
o 0.6
o 0.65
188. From a group of 5 men and 6 women, how many committees of size 3 are possible with two men and 1 woman if a certain man must be on the committee?
o 
· 
o 
o 
o None of these
189. Let  ,
, 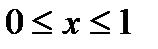 ,
,  , be the joint PDF of X and Y. Find the marginal PDF of Y.
, be the joint PDF of X and Y. Find the marginal PDF of Y.
· y+1/2
o y
o 1/2y
o y2/2
o 1/2
190. Let  ,
, 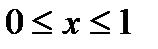 ,
,  , be the joint PDF of X and Y. Compute E[X].
, be the joint PDF of X and Y. Compute E[X].
o 0.2
· 0.823
o 0.583
o 1
o 0
191. Let  ,
, 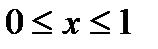 ,
,  , be the joint PDF of X and Y. Compute E[Y].
, be the joint PDF of X and Y. Compute E[Y].
o 0.2
· 0.823
o 0.583
o 1
o 0
192. Let  ,
, 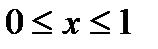 ,
,  , be the joint PDF of X and Y. Compute E[2X].
, be the joint PDF of X and Y. Compute E[2X].
· 7/6
o 0
o 1
o 7/12
o 1/6
193. Let X be continuous random variable with probability density function  . Find the expected value of random variable X.
. Find the expected value of random variable X.
o 19/3
o 13/3
o 12/7
· 28/9
o 27/4
194. The joint distribution for two random variables X and Y is given by  . Then find P(X>0.5).
. Then find P(X>0.5).
o 0.5
· 0.25
o 0.15
o 0.75
o 0.1
195. Probability mass function for discrete random variable X is represented by the 
graph. Find Var(X).
· 1
o 4
o 5
o 2
o 6
196. Two dice are rolled, find the probability that the sum is less than 13.
· 1
o 1.2
o 0.5
o 0.6
o 0.8
197. A bag has six red marbles and six blue marbles. If two marbles are drawn randomly from the bag, what is the probability that they will both be red?
o 1/2
o 11/12
o 5/12
· 5/22
o 1/3
198. A man can hit a target once in 4 shots. If he fires 4 shots in succession, what is the probability that he will hit his target?
· 175/256
o 1
o 1/256
o 81/256
o 144/256
199. Let random variable X be normal with parameters mean=5, variance=9. Which of the following is a standard normal variable?
o Z=(X-5)/5
o Z=(X-3)/5
· Z=(X-5)/3
o Z=(X-3)/3
o None of these
200. A coin is tossed 6 times. What is the probability of exactly 2 heads occurring in the 6 tosses.
· 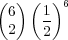
o 
o 
o 
o None of these
Date: 2015-12-11; view: 4769
| <== previous page | | | next page ==> |
| Example academic essay: The Death Penalty | | |