Exact Equations. Using an Integrating Factor.

Exact Equations

A region D in the plane is a connected open set. That is, a subset which cannot be decomposed into two non- empty disjoint open subsets. The region D is called simply connected if it contains no \holes." Alternatively, if any two continuous curves in D can be continuously deformed into one another. We do not make this precise here, but rely on standard intuition. A differential equation of the form M(x; y)dx + N(x; y)dy = 0 (1) is called exact in a region D in the plane if the we have equality of the partial derivatives My(x; y) = Nx(x; y) for all (x; y) (знак пренадлежит) D. If the region D is simply connected, then we can _nd a function f(x; y) de_ned in D such that fx = M; and fy = N: Then, we say that the general solution to (1) is the equation f(x; y) = C.

This is because the differential equation can be written as df = 0. Here we will not develop the complete theory of exact equations, but will simply give examples of how they are dealt with.

Example.

Find the general solution to

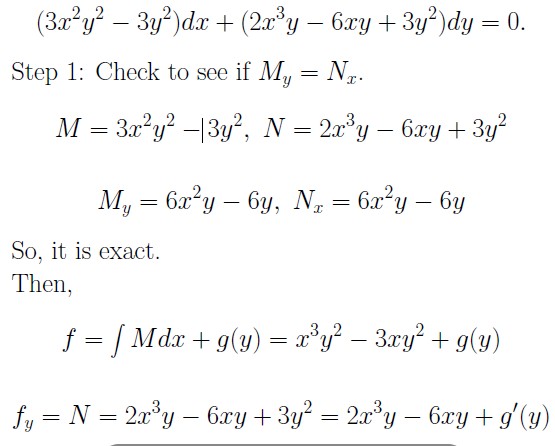
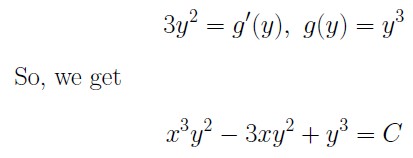as the general solution.

Integrating Factors

Sometimes a d.e. Mdx + Ndy = 0 is not exact, but can be made exact by multiplying by a non-zero function. Let us see when this can be done with functions of x or y alone. Consider a non-zero function µ(x) which is a function of x alone such that (µ M)y =

= (µ N)x We get µ yM + µ My = µ xN + µ Nx; µ y = 0 So, µ My = µ xN + µ Nx µ (My - Nx) = µ xN

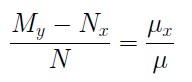Now, if the Left Hand Side is a function of x alone, say h(x), we can solve for µ (x) by

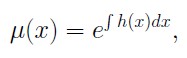and reverse the above arguments to get an integrating factor.

Similarly, if

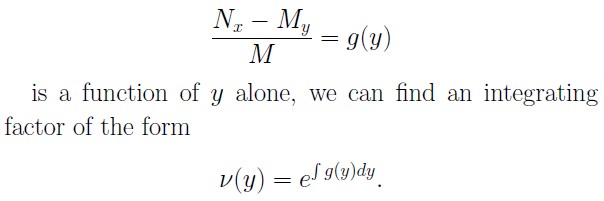
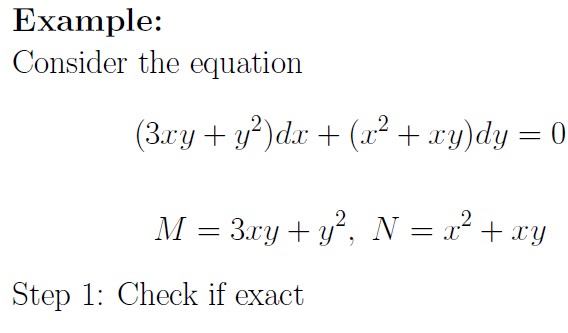
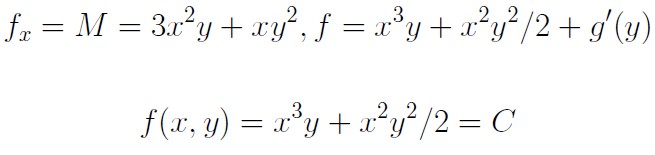
Date: 2015-04-20; view: 1155