
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Theme 3 PROPERTIES AND SOCIAL-ECONOMICAL RELATIONS
1) Calculate a determinant 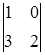 .
.
2) Calculate a minor 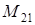 of an element
of an element 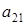 of a matrix
of a matrix  .
.
3) Calculate a determinant 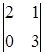 .
.
4) Find a matrix 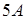 , if
, if 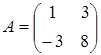 .
.
5) Calculate product of matrices 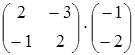 .
.
6) Find an inverse matrix 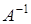 , if a matrix
, if a matrix 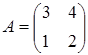 .
.
7) Calculate a determinant 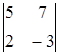 .
.
8) Matrices  and
and  are given. Find product of matrices
are given. Find product of matrices 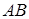 .
.
9) Matrices  and
and  are given. Find the sum of matrices
are given. Find the sum of matrices 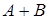 .
.
10) Find a matrix 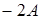 , if a matrix
, if a matrix 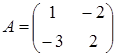 .
.
11) Find a matrix 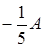 , if a matrix
, if a matrix 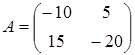 .
.
12) Determinant of a matrix  is the number, equal to:
is the number, equal to:
13) At transposing of a square matrix its determinant:
14) If elements of two lines are proportional, a determinant:
15) Solve the matrix equation  .
.
16) Find product of matrices 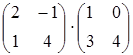 .
.
17) Find 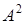 , if a matrix
, if a matrix 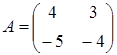 .
.
18) Determinant of the third order 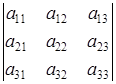 is equal:
is equal:
19) Calculate product of matrices 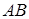 , if
, if 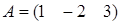 and
and  are given.
are given.
20) If  - a minor of a determinant of an element
- a minor of a determinant of an element 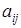 , then algebraic complement of this element
, then algebraic complement of this element 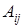 is equal:
is equal:
21) If in a determinant to change places of a lines, then:
22) If any line in a determinant to add with other line:
23) If in a determinant two columns are proportional, then:
24) To what value the determinant of an unitary matrix is equal?
25) Matrix  is given. Find an inverse matrix
is given. Find an inverse matrix 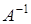 .
.
26) Calculate a determinant 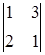 .
.
27) Calculate a minor 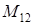 of a determinant
of a determinant 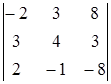 .
.
28) Calculate a determinant 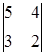 .
.
29) Calculate algebraic complement 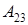 of a determinant
of a determinant 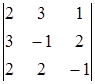 .
.
30) Find product of matrices 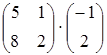 .
.
31) Find an inverse matrix 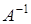 , if
, if 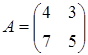 .
.
32) Find an inverse matrix 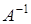 , if
, if 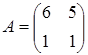 .
.
33) Find a matrix 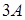 , if a matrix
, if a matrix  .
.
34) Calculate product of matrices 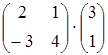 .
.
35) Find an inverse matrix 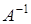 , if
, if 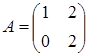 .
.
36) Matrix 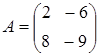 is given. Find the transposed matrix
is given. Find the transposed matrix  .
.
37) Calculate a determinant 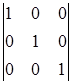 .
.
38) Calculate a determinant 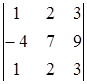 .
.
39) Ñalculate a minor 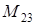 of an element
of an element 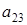 of a matrix
of a matrix  .
.
40) Minor is:
41) Calculate product of matrices: 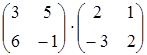 .
.
42) Matrices 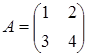 and
and 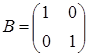 are given. Find product of a matrices
are given. Find product of a matrices 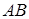 .
.
43) Matrices 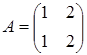 and
and 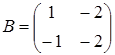 . Find a difference of matrices
. Find a difference of matrices 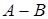 .
.
44) How to add two matrixes?
45) How to subtract one matrix from another matrix?
46) Matrices 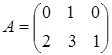 and
and 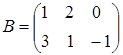 are given. Find
are given. Find 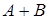 .
.
47) Matrices 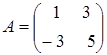 and
and 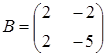 are given. Find
are given. Find 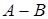 .
.
48) Calculate 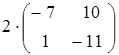 .
.
49) Calculate a determinant 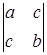 .
.
50) Calculate a determinant 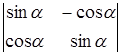 .
.
Theme 2. Systems of the linear equations
51) Solve system of the equations 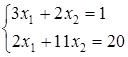 . Find
. Find  .
.
52) Solve system of the equations 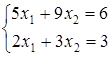 . Find
. Find  .
.
53) Solve system of the equations 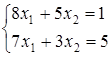 . Find
. Find  .
.
54) Solve system of the equations  . Find
. Find 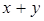 .
.
55) If the determinant of a matrix of system of the 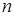 linear equations from
linear equations from 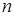 unknown variables is different from zero, then system of the equations :
unknown variables is different from zero, then system of the equations :
56) Solve system of the equations 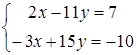 by Kramer's formulas. Find
by Kramer's formulas. Find  .
.
57) Find symbolical record of Kramer’s formulas, defining the decision of system if the determinant  of a matrix of system is not equal to zero.
of a matrix of system is not equal to zero.
58) System of the linear equations is called compatible, if it:
59) Solve system of the equations by Kramer's rule 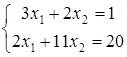 . Find
. Find  .
.
60) Solve system of the equations 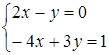 .
.
61) Solve system of the equations 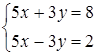 .
.
62) How it is possible to find 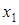 by means of Kramer's formula?
by means of Kramer's formula?
63) How it is possible to find 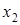 by means of Kramer's formula?
by means of Kramer's formula?
64) How it is possible to find  by means of Kramer's formula?
by means of Kramer's formula?
65) What from the specified formulas below is Kramer's formula?
66) Solve system of the equations 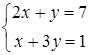 , using Kramer's rule.
, using Kramer's rule.
67) Solve system of the equations 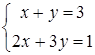 , using Kramer's rule.
, using Kramer's rule.
68) Solve system of the linear equations 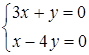 .
.
69) Solve system of the linear equations 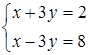 .
.
70) Solve system of the linear equations 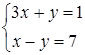 .
.
Theme 3. Elements of vector algebra
71) Points  and
and 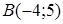 are given. Find coordinates of a vector
are given. Find coordinates of a vector 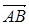 .
.
72) Find length of a vector  .
.
73) Vectors 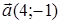 and
and  are given. Find coordinates of a vector
are given. Find coordinates of a vector 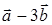 .
.
74) Find scalar product of vectors 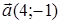 and
and  .
.
75) Find an angle between vectors 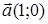 and
and 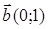 .
.
76) At what value  vectors
vectors  and
and 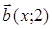 are collinear?
are collinear?
77) At what value  vectors
vectors  and
and 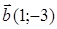 are orthogonal?
are orthogonal?
78)  ,
, 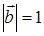 , an angle between
, an angle between 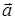 and
and 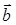 is equal
is equal 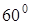 . Find scalar product
. Find scalar product 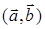 .
.
79) Points 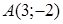 and
and 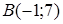 are given. Find coordinates of a vector
are given. Find coordinates of a vector 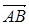 .
.
80) Find length of a vector 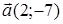 .
.
81) Vectors  and
and 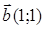 are given. Find coordinates of a vector
are given. Find coordinates of a vector  .
.
82) Find scalar product of vectors 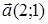 and
and 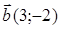 .
.
83) Find an angle between vectors 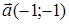 and
and 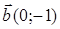 .
.
84) At what value 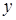 vectors
vectors 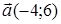 and
and 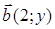 are collinear?
are collinear?
85) At what value 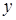 vectors
vectors 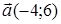 and
and 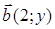 are orthogonal?
are orthogonal?
86) Points 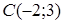 and
and 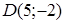 are given. Find coordinates of a vector
are given. Find coordinates of a vector  .
.
87) Find length of a vector 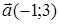 .
.
88) Vectors 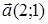 and
and 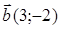 are given. Find coordinates of a vector
are given. Find coordinates of a vector 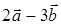 .
.
89) Find scalar product of vectors  and
and 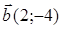 .
.
90) Find an angle between vectors 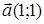 and
and  .
.
91) At what value  vectors
vectors 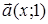 and
and 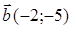 are collinear?
are collinear?
92) At what value  vectors
vectors 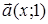 and
and  are orthogonal?
are orthogonal?
93) Vector, located on one straight line or parallel straight lines are called:
94) If vector have identical directions and length they are called:
95) Points 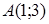 and
and 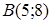 are given. Find coordinates of a vector
are given. Find coordinates of a vector 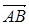 .
.
96) Find length of a vector  .
.
97) Vectors 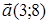 and
and 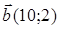 are given. Find coordinates of a vector
are given. Find coordinates of a vector  .
.
98) Find scalar product of vectors 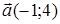 and
and 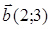 .
.
99) Find an angle between vectors  and
and 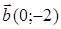 .
.
100) At what value  vectors
vectors 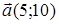 and
and 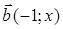 are collinear to each other?
are collinear to each other?
101) At what value  vectors
vectors 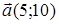 and
and 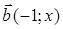 are orthogonal to each other?
are orthogonal to each other?
102) An angle between vectors 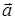 and
and 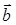 is found by the formula:
is found by the formula:
103) Scalar product of vectors 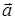 and
and 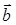 is equal:
is equal:
104) Scalar product of vectors 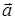 and
and 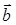 is equal to zero if:
is equal to zero if:
105) Points 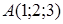 and
and 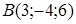 are given. Find length of a vector
are given. Find length of a vector 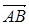 .
.
106) Find 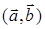 , if
, if 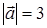 ,
,  ,
,  .
.
107) Vectors are called equipollent, if they:
108) Find scalar product of vectors 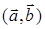 , if
, if  ,
, 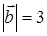 ,
, 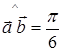 .
.
109) Find  , if
, if 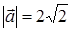 ,
,  ,
,  .
.
110) Find 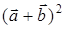 , if
, if 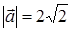 ,
,  ,
,  .
.
Theme 4. The equation of a line on a plane and in space
111) Points 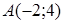 and
and 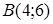 are given. Find coordinates of a midpoint
are given. Find coordinates of a midpoint 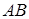 .
.
112) In what point the straight line 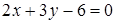 crosses an axis
crosses an axis 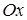 ?
?
113) Find angular coefficient of a straight line, parallel straight line 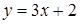 .
.
114) Write down the equation of the straight line, which is passing through points 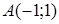 and
and 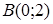 .
.
115) Find the equation of a straight line on a plane in a general view.
116) Find the equation of a straight line with angular coefficient.
117) Points 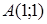 and
and 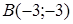 are given. Find coordinates of a midpoint
are given. Find coordinates of a midpoint 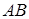 .
.
118) In what point the straight line 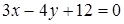 crosses an axis
crosses an axis 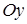 ?
?
119) Find angular coefficient of a straight line, parallel straight line 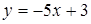 .
.
120) Write down the equation of the straight line, which is passing through points 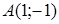 and
and 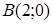 .
.
121) Points 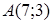 and
and 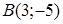 are given. Find coordinates of a midpoint
are given. Find coordinates of a midpoint 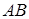 .
.
122) In what point the straight line 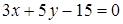 crosses an axis
crosses an axis 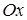 ?
?
123) Find angular coefficient of a straight line, parallel straight line 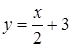 .
.
124) Write down the equation of the straight line which is passing through points 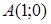 and
and 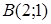 .
.
125) Find the equation of the straight line, which is passing through points 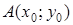 and
and  .
.
126) Find the equation of an axis 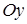 .
.
127) In what point the straight line 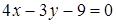 crosses an axis
crosses an axis 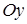 ?
?
128) Find angular coefficient of the straight line, parallel given straight line  .
.
129) Write down the equation of the straight line, which is passing through points 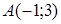 and
and 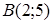 .
.
130) Calculate distance from a point 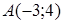 up to a straight line
up to a straight line 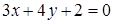 .
.
131) Find the equation of a straight line on a plane in segments.
132) Find coordinates of a midpoint, connecting points 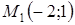 and
and 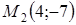 .
.
133) Two straight lines 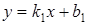 and
and 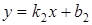 are parallel, if:
are parallel, if:
134) Write the equation of a straight line with angular coefficient 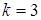 and passing through a point (2;-1).
and passing through a point (2;-1).
135) Write the equation of the straight line, which is passing through points 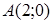 and
and 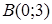 .
.
136) Find a point of crossing of straight lines 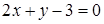 and
and 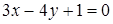 .
.
137) Find the equation of a straight line in segments for a straight line 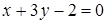 .
.
138) Points 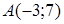 and
and 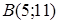 are given. Find coordinates of a midpoint
are given. Find coordinates of a midpoint 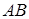 .
.
139) Find distance between points 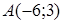 and
and 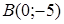 .
.
140) Construct the equation of the straight line, which is passing through a point 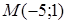 in parallel to the straight line
in parallel to the straight line  .
.
141) Find a point of crossing of straight lines 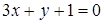 and
and  .
.
142) Construct the equation of the straight line, which is passing through a point 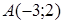 with angular coefficient 4.
with angular coefficient 4.
143) Find a point of crossing of straight lines 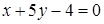 and
and 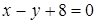 .
.
144) Find the equation of the straight line, which is passing through points 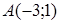 and
and 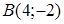 .
.
145) Find a condition of parallelism of straight lines 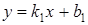 and
and 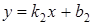 .
.
146) Find a condition of perpendicularity of straight lines 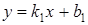 and
and 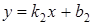 .
.
147) Equation of a straight line with angular coefficient is given by:
148) Find the equation of the straight line, which is passing through points 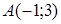 and
and 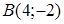 .
.
149) Find the equation of the straight line, which is passing through a point  , in parallel a vector
, in parallel a vector 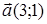 .
.
150) If 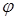 - an angle between straight lines
- an angle between straight lines 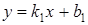 and
and  , what of following parameters expression
, what of following parameters expression 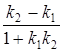 defines?
defines?
151) Find distance from a point 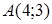 up to a straight line
up to a straight line 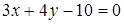 .
.
152) Find an angle between straight lines 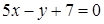 and
and 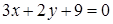 .
.
153) Find angular coefficient of a straight line, perpendicular straight line 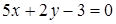 .
.
154) Find the equation of the straight line, which is passing through a point  and a parallel straight line
and a parallel straight line  .
.
155) Construct the equation of the straight line, which is passing through a point 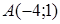 in parallel axes
in parallel axes 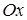 .
.
Theme 5. Function. Limits and a continuity
156) Find a limit 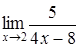 .
.
157) Find a limit 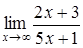 .
.
158) Find a limit 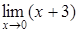 .
.
159) Find a limit 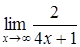 .
.
160) Find a limit 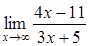 .
.
161) Find a limit 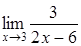 .
.
162) Find a limit 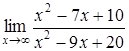 .
.
163) Find a limit 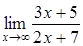 .
.
164) Ñalculate a limit 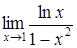 by means of Lhopital rule.
by means of Lhopital rule.
165) Ñalculate a limit 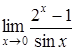 by means of Lhopital rule.
by means of Lhopital rule.
166) Ñalculate a limit 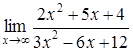 by means of Lhopital rule.
by means of Lhopital rule.
167) Find a limit 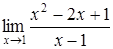 .
.
168) Find a limit 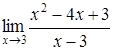 .
.
169) Find a limit 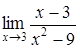 .
.
170) Find a limit 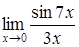 .
.
171) Find the first remarkable limit.
172) Find the second remarkable limit.
173) Find a limit 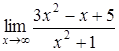 .
.
174) Ñalculate a limit 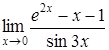 by means of Lhopital rule.
by means of Lhopital rule.
175) Find a domain of function 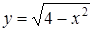 .
.
176) Find a domain of function 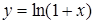 .
.
177) Find a limit 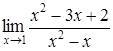 .
.
178) Find a limit 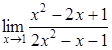 .
.
179) Find a limit 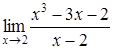 .
.
180) Find a limit 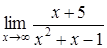 .
.
181) Find a limit 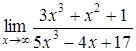 .
.
182) Find a limit 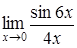 .
.
183) Find a limit 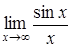 .
.
184) Ñalculate a limit 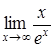 by means of Lhopital rule.
by means of Lhopital rule.
185) Ñalculate a limit 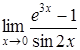 by means of Lhopital rule.
by means of Lhopital rule.
186) Ñalculate a limit 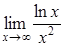 by means of Lhopital rule.
by means of Lhopital rule.
187) Find a limit  .
.
188) Find a limit  .
.
189) Find a limit  .
.
190) Find a limit  .
.
191) Find a limit 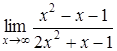 .
.
192) Find a limit 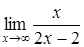 .
.
193) Find a limit  .
.
194) Find a limit 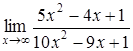 .
.
195) Find a limit 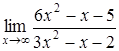 .
.
196) Find a limit 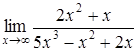 .
.
197) Find a limit 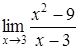 .
.
198) Find a limit 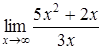 .
.
199) Find a limit 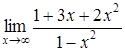 .
.
200) Find a limit 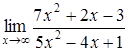 .
.
Theme 6. Derivative and differential of function
201) Derivative of function 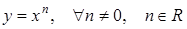 is equal:
is equal:
202) Find the formula of a derivative of quotient 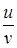 of two functions
of two functions 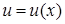 and
and 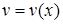 .
.
203) Find the formula of derivative of exponential 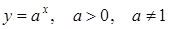 .
.
204) Find the formula of derivative of logarithmic function 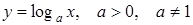 .
.
205) Find the formula of derivative of function 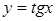 .
.
206) Find a derivative of function 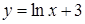 .
.
207) Find a derivative of function 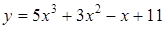 .
.
208) Function  is given. Ñalculate value
is given. Ñalculate value 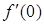 .
.
209) Find a derivative of function 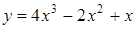 .
.
210) Function 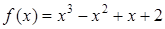 is given. Calculate value
is given. Calculate value 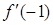 .
.
211) Find a derivative of function 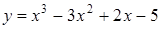 .
.
212) Find a derivative of function 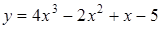 .
.
213) Function 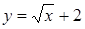 is given. Ñalculate value
is given. Ñalculate value 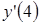 .
.
214) Function 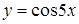 is given. Find
is given. Find 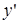 .
.
215) Function 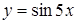 is given. Find
is given. Find 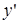 .
.
216) Function 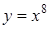 is given. Find
is given. Find  .
.
217) Function  is given. Find
is given. Find  .
.
218) Function 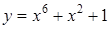 is given. Find
is given. Find  .
.
219) Find the formula of a derivative of product 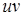 of two functions
of two functions 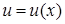 and
and 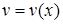 .
.
220) Find the formula of derivative 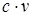 of function
of function 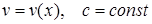 .
.
221) Function  is given. Calculate value
is given. Calculate value 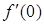 .
.
222) Find a derivative of function 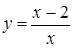 .
.
223) Find a derivative of function  .
.
224) Find differential of function 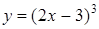 .
.
225) Find a derivative of function 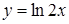 .
.
226) Function 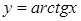 is given. Find a derivative
is given. Find a derivative 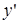 .
.
227) Derivative of function 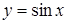 is equal:
is equal:
228) Derivative of function 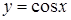 is equal:
is equal:
229) Derivative of function 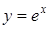 is equal:
is equal:
230) Derivative of function 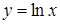 is equal:
is equal:
231) Derivative of function 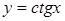 is equal:
is equal:
232) Derivative of function 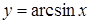 is equal:
is equal:
233) Derivative of function 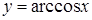 is equal:
is equal:
234) Derivative of function 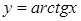 is equal:
is equal:
235) Derivative of function 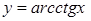 is equal:
is equal:
236) Find a derivative of function 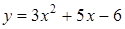 .
.
237) Find a derivative of function  .
.
238) Find a derivative of function  .
.
239) Find a derivative of function 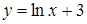 .
.
240) Find a derivative of function 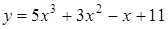 .
.
241) Find a derivative of function 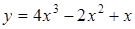 .
.
242) Find a derivative of function 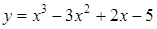 .
.
243) Find a derivative of function 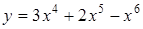 .
.
244) Find a derivative of function 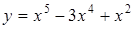 .
.
245) Find a derivative of function 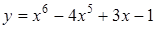 .
.
Theme 7. Investigation of function by means of a derivative
246) Find an interval of decrease of function 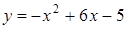 .
.
247) Find an interval of increase of function 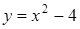 .
.
248) Find an interval of increase of function 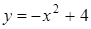 .
.
249) Find an interval of convexity of function  .
.
250) Find an interval of concavity of function  .
.
251) Find an interval of convexity of function 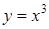 .
.
252) Find an interval of concavity of function 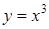 .
.
253) Find a point of a maximum of function  .
.
254) Find a point of a minimum of function 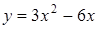 .
.
255) Investigate function 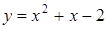 on an extremum.
on an extremum.
256) If the derivative of differentiate function is positive inside of an interval 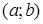 , then function on an interval
, then function on an interval 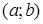 :
:
257) Necessary condition of an extremum of function in a point 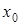 :
:
258) If at transition through a critical point 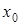 the derivative of function changes the sign from plus on a minus, then the point
the derivative of function changes the sign from plus on a minus, then the point 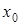 is a point:
is a point:
259) Find interval of increase of function  .
.
260) Find a point of a minimum of function 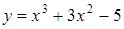 .
.
261) Find a point of a maximum of function 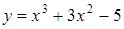 .
.
262) Find interval of decrease of function  .
.
263) Find points of inflection of function 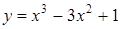 .
.
264) Find points of inflection of a curve  .
.
265) Find an interval of convexity of the graph of function 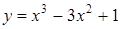 .
.
266) To what of following equality even function satisfies:
267) To what of following equality odd function satisfies:
Theme 8. Functions of several variables
268) Function 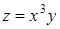 is given. Find a partial derivative
is given. Find a partial derivative 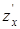 .
.
269) Function 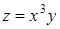 is given. Find a partial derivative
is given. Find a partial derivative 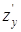 .
.
270) Function 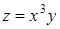 is given. Find a partial derivative
is given. Find a partial derivative 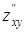 .
.
271) Function 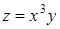 is given. Find a partial derivative
is given. Find a partial derivative 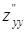 .
.
272) Function 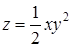 is given. Find a partial derivative
is given. Find a partial derivative 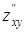 .
.
273) Function 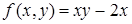 is given. Find
is given. Find 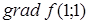 .
.
274) Function  is given. Find
is given. Find 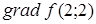 .
.
275) Function 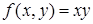 is given. Find
is given. Find 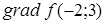 .
.
276) Find a critical point of function 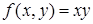 .
.
277) Find a critical point of function 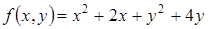 .
.
278) Function  is given. Find a partial derivative
is given. Find a partial derivative 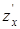 .
.
279) Find the formula of total differential of function  .
.
280) Function 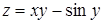 is given. Find a partial derivative
is given. Find a partial derivative 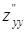 .
.
281) Find a critical point of function 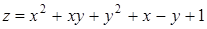 .
.
282) Find a critical point of function 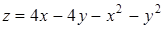 .
.
283) Find a domain of function  .
.
284) Find a domain of function 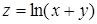 .
.
285) Function  is given. Find a partial derivative
is given. Find a partial derivative 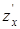 .
.
286) Function 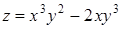 is given. Find a partial derivative
is given. Find a partial derivative 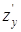 .
.
287) Find total differential of function 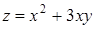 .
.
288) Function 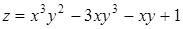 is given. Find a partial derivative
is given. Find a partial derivative 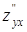 .
.
Theme 9. Antiderivative and indefinite integral
289) Find integral 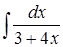 .
.
290) Find integral  .
.
291) Find integral 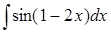 .
.
292) If 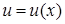 and
and 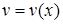 are differentiable functions, then
are differentiable functions, then  is equal:
is equal:
293) Find integral 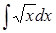 .
.
294) Find integral 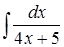 .
.
295) Function  is called antiderivative of function
is called antiderivative of function 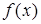 on an interval , if function
on an interval , if function  is differentiable on
is differentiable on  and following equality is executed:
and following equality is executed:
296) Integral 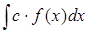 is equal:
is equal:
297) Integral 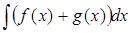 is equal:
is equal:
298) Integral 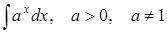 is equal:
is equal:
299) Find expedient substitution for a finding of integral 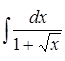 .
.
300) Find integral 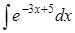 .
.
301) Find integral 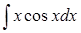 .
.
302) Formula of integration in parts for indefinite integral is given by:
303) Find integral 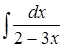 .
.
304) Find integral 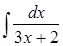 .
.
305) Find integral 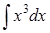 .
.
306) Find integral 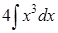 .
.
307) Find integral 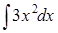 .
.
308) Find integral 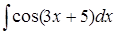 .
.
309) Find integral  .
.
310) Integral 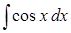 is equal:
is equal:
311) Find integral 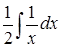 .
.
312) Find definition of indefinite integral.
313) Integral 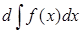 is equal:
is equal:
314) Integral 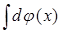 is equal:
is equal:
315) Integral 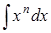 is equal:
is equal:
316) Integral  is equal:
is equal:
317) Integral 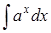 is equal:
is equal:
318) Integral 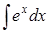 is equal:
is equal:
319) Integral 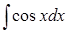 is equal:
is equal:
320) Integral 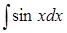 is equal:
is equal:
321) Find integral 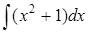 .
.
322) Find integral 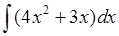 .
.
323) Find integral  .
.
324) Find integral 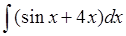 .
.
325) Find integral 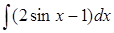 .
.
326) Find integral 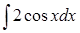 .
.
Theme 10. Definite integral and its applications
327) Calculate integral 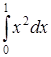 .
.
328) Calculate integral 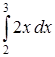 .
.
329) Find geometrical meaning of the definite integral 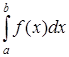 .
.
330) Find the area of the figure, limited by a parabola 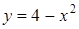 and an axis using definite integral.
and an axis using definite integral.
331) Calculate integral  .
.
332) Calculate integral 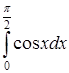 .
.
333) Calculate the area of the figure, limited by lines  ,
, 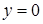 ,
, 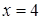 .
.
334) Calculate the area of the figure, limited by lines  ,
,  .
.
335) Calculate the area of the figure, limited by lines 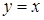 ,
,  ,
, 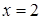 .
.
336) Calculate improper integral 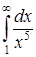 or establish its divergence.
or establish its divergence.
337) Calculate improper integral 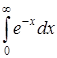 or establish its divergence.
or establish its divergence.
338) Calculate improper integral  or establish its divergence.
or establish its divergence.
339) Calculate improper integral 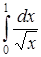 or establish its divergence.
or establish its divergence.
340) Calculate improper integral 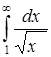 or establish its divergence.
or establish its divergence.
341) Let function 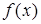 is integrated on a segment
is integrated on a segment 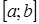 , then function
, then function 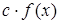 also is integrated on this segment and following equality is executed:
also is integrated on this segment and following equality is executed:
342) Let functions 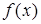 and
and 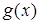 are integrated on a segment
are integrated on a segment 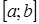 , then function
, then function 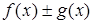 also is integrated on the given segment and following equality is executed:
also is integrated on the given segment and following equality is executed:
343) What of following equality is correct?
344) Formula of Newton – Leibniz is given by:
345) Formula of integration in parts for definite integral is given by:
346) Calculate integral 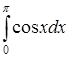 .
.
347) Find value of integral 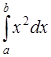 .
.
348) Calculate integral 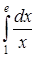 .
.
349) Integral 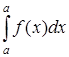 is equal:
is equal:
350) Calculate integral 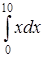 .
.
351) Find value of integral 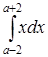 .
.
352) Calculate integral 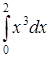 .
.
Theme 11. Differential equations and series
353) Define type of the differential equation in a general view 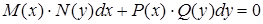 .
.
354) Define type of the differential equation 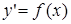 .
. 
355) Define type of the differential equation 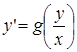 .
.
356) Define type of the differential equation 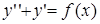 .
.
357) Define type of the differential equation 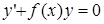 .
.
358) Differential equation 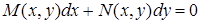 is called homogeneous, if:
is called homogeneous, if:
359) What is order of the differential equation?
360) Linear differential equation of the first order is the equation of a kind:
Theme 3 PROPERTIES AND SOCIAL-ECONOMICAL RELATIONS
1. Property in economical and legal sense
2. Classification of the property
3. Macroeconomical structure of the property
1. Property in economical and legal sense
The property is rather difficult appearance: economical theory analyze the economical content of this appearance, and jurisprudence - legal.
In economical sense the property is a human relations on appropriation and economic usage of the material and non-material benefits. The property in legal understanding demonstrates how real property relations are arranged and fixed in precepts of law and laws which are established by the state in order for all citizens.
Property as economical system. In each economical relation of the property there are two sides: the subject (owner) and object (property). Appropriation relations are spread primarily to the such property on which economic activities directly depend. It includes production factors (both material benefits, and results of intellectual transactions).
Studying of the property allows to give an answer to three principal social and economic problems:
1. Who (what subjects of activities) has an economical power - appropriate the factors and results of production ?
2. What kind of economical relations give an ability on the best usage of the property?
3. Who will take incomes of economical activities?
So, the system of economical relations of the property includes following elements: A) appropriation of factors and results of production; B) economical usage of the material and other means; C) property income (Figure 1).
 Appropriation - economical rela-tions between people which estab-lishes their relation to things as to their own. This relation consist the base of productive process. Because any material benefit production means an appro-priation by people of the material of nature and energy in a purpose of consumption of their needs.
Appropriation - economical rela-tions between people which estab-lishes their relation to things as to their own. This relation consist the base of productive process. Because any material benefit production means an appro-priation by people of the material of nature and energy in a purpose of consumption of their needs.
Estrangement relation is opposite to appropriation. It has appeared, if any part of a society occupied all factors of productions, and other part remains without any livelihood. Or when the goods created by one people, appropriates by other.
Owners of factors of productions are not always engaged in creative activity. They give the chance to other persons to use their property (for example, land, house, the equipment) in the economic purposes under certain conditions. In this case between the owner and entrepreneur appeared relations of economic usage of property. Last has an opportunity to temporarily own and use object by another's property. It can be, rent - hire by one person (or by enterprise) at other person (or enterprise) the property in temporary using on certain period and for a certain price.
The property economically justifies itself if brings an income to its o
Date: 2014-12-28; view: 1061
| <== previous page | | | next page ==> |
| Theme 1. Matrices and determinants | | | Classification of the property |