Teaching the Productive Skills

QUESTIONS TO THINK ABOUT

1. Why do people engage in talking to each other?

2. What do you think “effective communication” is?

3. Do you think that all speaking and writing has a “purpose”?

4. Two students are acting out a dialogue in the classroom. Do you think a teacher can intervene and correct a mistake?

5. While at school, did you like drills (mechanical and not very creative exercises)?

CHAPTER OUTLINE

· The Nature of Communication

· The Information Gap

· Characteristics of Communicative Activities

· Stages in Language Teaching

· Ways of Getting Students to Practice Oral English

CHAPTER GOALS

After completing this chapter, you should be able to

1. explain the nature of communication

2. define the concept of “information gap”

3. name six characteristics of communicative activities

4. describe stages in language teaching

5. give examples of how you can get students to practice oral English

KEY WORDS

communication; information gap; a communicative purpose; variety of language; teacher intervention; materials controls; practice activities; oral drills; personalization and localization

· The Nature of Communication

Communication between humans is an extremely complex and ever-changing phenomenon. There are certain generalizations that we can make about the majority of communicative events. They will have particular relevance for the teaching of languages. When 2 people are engaged in talking to each other we can be fairly sure that they are doing so for good reasons. What are these reasons?

o They want to say something

o They have some communicative purpose. They say things because they want something to happen as a result of what they say.

o They select from their language store. Speakers have a huge capacity to create new sentences. In order to achieve this communicative purpose they will select the language they think is appropriate for this purpose (from the “store” of language they posses).

These three generalizations apply equally to someone having a private conversation and to the politician giving a speech to thousands. They apply to the schoolteacher and the radio announcer, the judge and the shop assistant.

It is important to realize that these generalizations do not only apply to the spoken word: they characterize written communication as well, and although a difference may be that the writer is not in immediate contact with the reader (whereas in a conversation two or more people are together), the same also applies to the example of the radio announcer, and, to some extent, the academic giving a lecture in a hall. We can also make some generalizations about a listener (or reader) of language. By effective communication we mean that there is a desire for the communication to be effective both from the point of view of the speaker and the listener. Of course there are many other characteristics that are necessary for effective communication and there are many possible reasons for breakdown in communication, but once again three points can be made about the listeners:

o They want to listen to “something”. Once again “want” is used in a general way. But in order for someone to understand what they are listening to (or reading) they must have some desire to do so.

o They are interested in the communicative purpose of what is being said. In general people listen to language because they want to find out what the speaker is trying to say – in other words what ideas they are conveying.

o They process a variety of language. Although the listener may have a good idea of what the speaker is going to say next he or she has to be prepared to process a great variety of grammar and vocabulary to understand exactly what is being said.

Once again these comments apply generally to all listeners, and are equally true of readers.

Whenever communication takes place, of course, there is a speaker (and/or writer) and a listener (and/or reader). This is the case even where a writer writes a novels for here the writer assumes that there will be a reader one day and that that reader will be performing a communicative act when reading the book.

Our generalizations about the nature of communication are presented in the Figure below.

The nature of communication

When organizing communicative activities we will try to ensure that these activities share the characteristics we have mentioned here. We will discuss this further in chapters 11 and 12.

· The Information Gap

We have said that speakers normally have a communicative purpose and that listeners are interested in discovering what that purpose is. However, even if listeners have some idea about the purpose, they must listen in order to be sure. We can illustrate this with a simple example. Consider the following example in which a man (A) speaks to a woman (B) at a bus stop:

A: Excurse me.

B: Yes?

A: Do you have a watch?

B: Yes . . . why?

A: I wonder if you could tell me what the time is?

B: Certainly . . . it’s six o’clock.

A: Thank you.

B: You are welcome.

The man who starts the conversation may have many reasons for speaking: he may want to get into conversation with the woman because he thinks she looks interesting, and the question about the time may simply be a pretext for this. On the other hand he may genuinely want to know the time. In both cases there exists an information gap between what A and B know. If the question about the time is a genuine one we can say that B has information that A doesn’t have (the time) and A wants that information. In other words there is a gap between the two in the information they possess, and the conversation helps to close that gap so that now both speakers have the same information. But even if this were not the real purpose of the conversation there is still a gap between the speakers where B does not know what A’s purpose is before he speaks.

In the classroom we will want to create the same kind of information gap if we are to encourage real communication. Many of the activities in the next two chapters will be designed so that there is an information gap between the participants. This insures lifelike communication to some extent.

· Characteristics of Communicative Activities

Having discussed the nature of communication we can now suggest characteristics that are necessary for communicative activities.

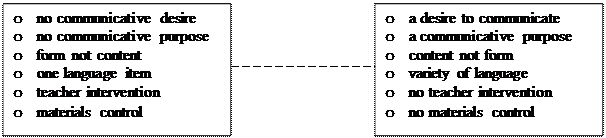
Whatever activity the students are involved in, the students should have a desire to communicate. The students should also have some kind of communicative purpose. If students do have a purpose then their attention should be centered on the content of what is being said or written and not the language form that is being used. The students will have to deal with a variety of language rather than just one grammatical construction, for example. While the students are engaged in the communicative activity the teacher should not intervene. By “intervene” we mean telling students that they are making mistakes, asking for repetition, etc. This would undermine the communicative purpose of the activity. The teacher should not control the materials which students are using and the teacher should not restrict the students’ choice of what to say and how to say it.

We can summarize the points we have made in the following figure:

NON-COMMUNICATIVE COMMUNICATIVE

ACTIVITIES ACTIVITIES

· Stages in Language Teaching

We will divide work on the productive skills into three major stages, introducing new language, practice, and communicative activities.

o Introducing new language

Here the teacher will work with controlled techniques, asking students to repeat and perform in drills. At the same time the teacher will insist on accuracy, correcting where students make mistakes. Although these introduction stages (often called presentation) should be kept short they are nevertheless important in helping the students to understand facts about new language – vocabulary and grammar.

o Practice

Practice activities often have some features of both-communicative and communicative activities. During practice activities the teacher may intervene slightly to point out inaccuracy.

o Communicative activities

Communicative activities are those which exhibit the above mentioned six characteristics. Such activities are vital in a language classroom since here the students can do their best to use the English language as individuals. We will look at activities of this kind in the next chapter.

· Ways of Getting Students to Practice Oral English

We will look at ways of getting students to practice oral English. We will consider oral drills, information gap activities, games and personalization and localization.

o Oral drills

Drills are usually very controlled and therefore they have limited potential. Because they are fairly repetitive and not very creative they should not be used for too long or too frequently. However, they do give students the opportunity for ‘safe’ practice.

Chain drills

Chain drills are ways of practicing a particular structure over and over again in the context of either a game or a personal element.

Students can sit in groups. The teacher chooses the structure and then says (for example):

‘My name’s Olena Petrivna and I’d like to travel round the world.’

The student next to the teacher then has to say:

‘My name’s Pavlo and I would like to learn Chinese.’

‘Her name’s Olena Petrivna and she’d like to travel round the world.

The third student then has to remember the first two speaker’s ambitions and then give his or her own. Chain drills are an amusing way of getting quick and involving practice of a particular structure. If the memory element is added (as in our example here) they can be made into a game.

Drill work is very useful since it provides opportunities for students to practise a new bit of language in the most controlled way. Most drills can be adopted for pairwork and groupwork.

But it is important to remember the limitations of drills and to use them sparingly.

o Information gap activities

With information gap activities different students are given different bits of information. By sharing this information they can complete a task.

Information gap activities, in other words, are drills, but because they have a slightly communicative element built into them they are more involving and motivating than a lot of question and answer practice.

Below we give an example of the activity which is called “Application”.

Application

This information gap activity is designed for intermediate students and shows how such an activity can be used not only for oral practice but also for reading and form-filling.

Students are divided into pairs. They are told not to look at each other’s papers. Then they are told that they must each complete the paper in front of them (the paper is the same application form but with different words in each form blanked out).

The material makes students ask each other a large number of questions in order to complete their task. In order to ask these questions both students have to read their material and work out what questions to ask.

This is a good example of an information gap exercise which integrates reading and speaking skills.

So, information gap tasks provide students with a reason to communicate with each other, and can be designed to practise more or less specific language.

Games

Games are a vital part of a teacher’s equipment, not only for the language practice they provide, but also for the therapeutic effect they have. They can be used at any stage of a class to provide an amusing and challenging respite from other classroom activity, and are especially useful at the end of a long day to send the students away feeling cheerful about their English class. We will look at two well-known examples.

Ø Ask the right question

Students are divided into pairs in which there is A and B. Student A in each pair is given cards such as the following:

Student A then has to ask B questions so that B gives exactly the answer written on A’s card. If B fails to give the exact answer A has to ask the question again until B gets it exactly right.

This game, suitable for all levels is great fun and quite difficult since A has to think of exactly the right question to get exactly the right answer.

Ø Twenty questions

Twenty questions is a team game which originated from a popular BBC radio programme.

Students are divided into teams. Each team must think of a number of objects. The game starts when one person from Team A asks someone from Team B a question which can only be answered with ‘yes’ or ‘no’.

If Team B finds out what the object is after only a maximum of fifteen questions they get two points. If it takes them between sixteen and twenty questions they get one point. They get no points if they do not discover what the object is after asking twenty questions.

There are many varieties of this game. Instead of objects the teams could be thinking of famous people and the questions could start with ‘Is this person a man?’ (notice that ‘Is this person a man or a woman?’ is not acceptable because it is not a ‘yes/no’ question).

o Personalization and localization

Personalization and localization refer to those stages of practice where students use language they have recently learnt to talk about themselves and their lives. Such stages can obviously be very controlled or very free.

Language teaching materials in general sometimes give students a highly grammatical (and not very real) idea of how questions are asked and answered. Students practise questions such as ‘Do you smoke?’ and are expected to answer ‘Yes I do/No I don’t’.

Research has suggested that answers to questions in real life are seldom grammatically parallel to the questions. The answer to a question such as ‘Are you happy?’ is seldom ‘Yes I am/No I am not’. Much more likely are responses such as ‘More or less’, ‘Can’t complain’ or even ‘Why do you ask?’

Teachers should encourage this type of response and a way of doing so is to insist on an additional remark being made. This means that where a student gives a yes/no type answer he or she must then add a comment to it. The following example shows such a remark being prompted:

S2: Do you like swimming?

S1: Yes.

T: Yes . . . and?

S1: Yes . . . I go to the swimming-pool twice a week.

During personalization and localization stages the teacher can prompt the use of additional remarks and follow-up questions in order to encourage realistic communication. We will now look at one example of ‘The hot seat’.

In this activity a student is put in the ‘hot seat’ and subjected to a barrage of questions. Obviously the technique has to be used sensitively by the teacher, but in the right atmosphere and carried out in the right spirit the activity provides enormous opportunity for practice.

A student is selected to be the focus of attention. The idea is to get students to ask him or her as many questions as they know, for example:

T: OK Irina . . . ask Olena about yesterday evening.

S1: What did you do yesterday evening, Olena?

S2: I went to the supermarket.

(Pause)

T: Well Irina . . .

S1: Oh . . . why?

S2: Because I needed some things.

S3: What did you buy?

S2: Eggs . .milk. . . that kind of thing. etc.

Any subject of current interest can be used for such a lesson and it will be suitable for the beginning classes particularly, where it will serve to “warm the class up”.

Date: 2015-02-28; view: 3421