Chapter 3 Statically Determine Beams

The suspension method used for constructing bending moment diagram of the simple beam AB can be employed to construct the bending moment diagram of the segment AB shown in Fig.3.8. Therefore, for a segment of a member, the moment diagram may be constructed as follows.

Firstly, determine the end moments 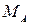at section A and 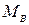at section B of the segment and take the end couples 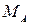and 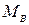as ordinates (indicate on tension side of the segment), draw a straight dashes line which represent the 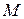diagram.

Secondly, take the dashed line as the base line, superimpose the ordinates ( in the direction perpendicular to AB ) of the diagram, we accomplish the final M diagram of segment AB.

EXAMPLES 3-4

Construct the bending moment diagram for the overhanging beam shown in Fig.3.9 (a).

Solution

It is necessary for constructing bending moment diagram to find reactions.

1. Determination of bending moments of control sections.

The section A, B and D are control sections at which loads vary discontinuously, which divide the beam into two segments AB and BD. By the method of sections we obtain the bending moments.

(tension in the upper fibers)

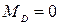
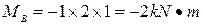(tension in the upper fibers)

2.Consstructing bending moments diagram segment by segment.

Take axial line AD as the abscissa axis; indicate the location of control segment (A,B and D ); lay off the ordinates at points A,B and D on tension side of the beam by the magnitudes of 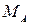, 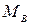and respectively, we obtain points 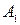, and .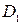

Connect points 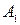, and 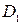with dashes lines, then take the dashed lines as base lines and impose the ordinates of corresponding bending moment diagram 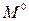(x). The final bending moment diagram is shown as in Fig.3.9 (b).

Note that since a concentrated load of 4kN is applied at the middle of the segment AB, the bending moment diagram 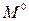(x) in a segment AB should be that of a simple beam with a same span of AB and subjected to the same external load of segment AB (i.e., a simple beam with a span of 5m and subjected to concentrated downward force of 4kN at the middle of the beam). While the bending moment diagram 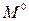(x) is segment BD should be that of a simple beam with the same span of BD and subjected to the same uniformly distributed load of a segment BD (i.e., a simple beam with a span of 2m and subjected to uniformly distributed load of 1kN/m in the whole span of beam).

3.3 The analysis of Simply supported Inclined Beams

Knowing from strength of materials, the bending moment value 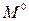at the middle of segment AB will be 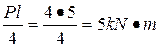, the total value of the bending moment at section C will be

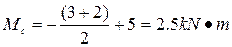(tension in the lower fibers)

The bending moment value 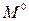at the middle of segment BD will be 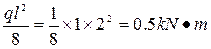, the total value of the bending moment at the middle section E will be

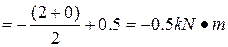(tension in the upper fibers)

The bending moment diagram in the segment BD can be plotted by considering the segment as a cantilever beam and directly drawing the moment diagram with no need of method of superposition as well.

3.3 The Analysis of Simply Supported Inclined Beams

In the civil engineering constructions, inclined beams shown as in Fig.3.10 (b) and (c), are commonly used as the analyzing models of stairs.(Fig.3.10(a)).

The axial line of an inclined beam is straight slope line; its slope angle is denoted by 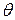. The loads imposed to the inclined beams can be classified into two groups:: (1) vertically distributed loads along the axial lines of inclined beams, such as deadweight loads; (2) vertically distributed loads along the horizontal lines (the projections of axial lines of inclined beams), such as live loads. In order to facilitate the analysis, vertically distributed loads along the axial line of inclined beams are usually altered to vertically distributed loads along the horizontal projections of the beams. The final analyzing results under the action of vertically distributed loads along the horizontal projections of the beams. If the distributed loads are uniformly distributed the alternative relationship of this two kinds loads will be

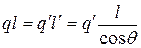
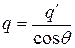
Date: 2015-02-28; view: 785