Coulomb criterion

The part of the Mohr envelop located in the compressive domain (s > 0) is close to a straight line whose equation (or Coulomb criterion) is the following (Figure):

t_c = C + m s_nc

where C is the cohesion of the material, giving the magnitude of the shear stress (t_c) necessary to break the material at zero (atmospheric) pressure ; or magnitude of the binding force to be overcome before rupture. m is the slope of the Coulomb straight line ; it is called the internal friction : it gives the magnitude of the rugosity of the fault surface, or the intensity of the friction experienced by the fault under a given normal stress s_nc ; the angle of this slope (j = tg^-1 m) is called internal friction angle.

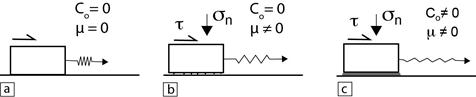
Figure. Illustration of the Coulomb law : t_c = C + m s_nc. a : no friction (on the fault surface), no cohesion : t_c = 0. b : no cohesion, but friction is non zero : t_c will depend on the load (s_n). c : by adding a cohesion, an initial shear stress is necessary to « unglue » the fault-plane before mouvement as in b.

By construction of the Mohr circle, a is the angle between the fracture plane and the maximum compressive stress (s₁). Note that 2a (j + 2a = 90°) (Figure) : meaning that the least friction on the fault plane (j = 0), the closest to 45° is the fault plane (maximum shear stress on the fault plane).

The case of no friction (horizontal Coulomb line) along with a non-zero cohesion corresponds to an ideal clay material. The case of zero cohesion along with a strong internal friction corresponds to an ideal granular material like sand.

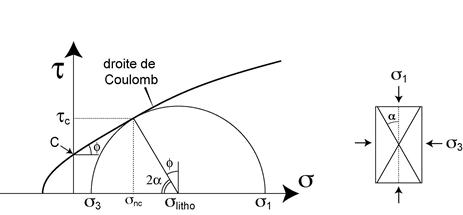
Figure 7.4 : Mohr envelop of a material. The linear part corresponds to the Coulomb behaviour. j : friction angle. a is the angle between s₁ and the fracture plane.

A look at the (experimental) Mohr envelop shows that, in the tensional domain (s < 0), or that of t_c ≤ C, the Coulomb criterion is not adapted to describe the reality of rupture : rupture in tension does not follow the Coulomb law. Also, the Coulomb law is not adapted for large confining pressures (right side of the (t,s) diagram) where the slope of the envelop (friction) decreases. These two aspect are examined in the next paragraphs.

Date: 2014-12-28; view: 1185