II. FRACTURE MODES

Deformation of cylindrical rock specimens subjected to a vertical stress (s₁, using a hydraulic press) tells us that (for an isotropic material and according to the magnitude of the applied pressure) different modes of fractures appear (Figure). If the experiment is performed at the atmospheric pressure (i.e. in absence of a confining pressure, hence at s_litho = 1 bar = 0.1 MPa) the specimen will develop fractures roughly parallel to the imposed load (i.e. vertical). Such an experiment is called « uniaxial » compression : s₁ ≥ s_litho). Note that vertical fractures appear only if there is no friction on sides of the pressed specimen. This fracture mode corresponds to fracture opening perpendicularly to the fracture plane ; it is called the extension mode (or mode I : Fig.a).

If a confining pressure is added by constraining the specimen in a talc, halite … or gaz … medium, in order to transmit a hydrostatic (isotropic) pressure, the experiment becomes pseudo-triaxial (s₁ ≥ s₂ = s₃). By increasing the confining pressure (s_litho) and the vertical stress (s₁) on the same time, rupture takes place through fractures that a inclined with respect to the axis of the cylinder, and that tend to move parallel to themselves. Fracturation tends to a shear mode (modes II or III ; Fig.b).

By increasing the confining pressure, such fractures become abundant and displacement along each fracture decreases. Fractures tend to be symmetrically inclined with respect to the specimen axis (symmetry with respect to s₁). They are called conjugate fractures. Their angle with respect to s₁ never exceeds 45° (Fig.c). Note that these fractures are made of a myriad of minute segments parallel to s₁.

Finally, for large confining pressures, the fracture density increases, and the movement along each fracture does not seem significant. However, total displacement may be important. The resulting deformation appears to be homogeneous (at least to our scale of observation) : it is said « penetrative » (Fig.d). The mechanical behaviour of the specimen looks like ductile but, at the microscopc scale, it remains discontinuous (small displacements along fissures can still be observed).

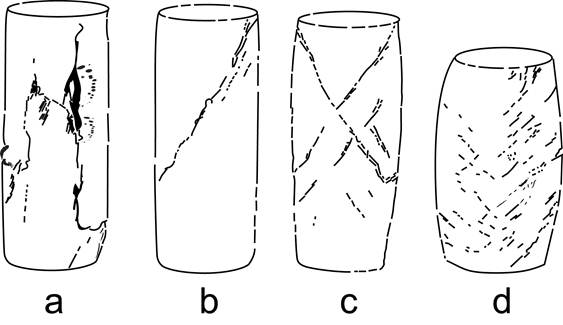
Figure. Expérimental fracturation of a marble at increasing confining pressures. Load applied vertically. a : Extension fracture at 1 atm (0.1 MPa). b : Shear fracture at 3.5 MPa confining pressure. c and d : Conjugate shear fractures at 35 MPa et 100 MPa confining pressures (After Paterson, 1958).

In the strain/stress graph reporting these experiments (Figure) it can be observed that both the elastic threshold and the ductile domain increase with increasing confining pressure.

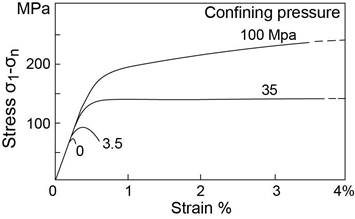
Figure. Applied differential stress versus strain for the experiments described hereabove. Both the elastic limit and the domain of ductile deformation are observed to increase with increasing confining pressure.

These results can be generalized to pure triaxial experiments (s₁ ≥ s₂ ≥ s₃ ; common in nature but difficult to reproduce in laboratory) : the extension fractures contain s₁ and s₂ (or are perpendicular to s₃) and the shear fractures contain s₂, and are oblique with respect to s₁ and s₃ (Figure). This (realistic) geometrical description is called the Anderson’s model (1951).

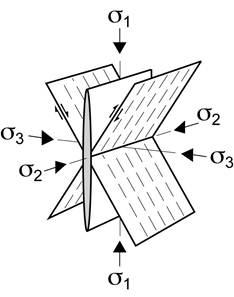
Figure. Orientation relationships between fractures and principal stress components (s₁ ≥ s₂ ≥ s₃). Open fracture: tension fracture; Striated planes: shear fractures.

This Andersons’s model is at the base of graphical determination of the orientations of s₁, s₂ and s₃ using sets of measured fractures in the field (provided that it can be proved that these fractures are contemporaneous, i.e. derive from the same dynamic event).

Date: 2014-12-28; view: 2545