
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Appendix B. Tutorial in Number Theory
This appendix consists of an overview of the number theoretic results used in this book. Most of the proofs are very easy and can be found, for instance, in [Ko].
An integer a divides another integer b, in symbols a | b, iff b = da holds for some integer d. Then a is called a divisor or factor of b. Let a be an integer greater than 1. Then a is prime if its only positive divisors are 1 and a, otherwise a is composite. Every integer n > 1 can be represented uniquely, disregarding the order of factors, as a product of primes. The essential fact from the point of view of cryptography is that no tractable factorization algorithms are known although, on the other hand, no nontrivial lower bounds for the time complexity of factorization have been established. No tractable methods are known even for the simple case, where two primes p and q have to be recovered from their product n = pq.
The greatest common divisor of a and b, in symbols g.c.d. (a, b) or briefly (a, b), is the largest integer dividing both a and b. Equivalently, (a, b) is the only positive integer that divides a and b and is divisible by any integer dividing both a and b. Similarly, the least common multiple l.c.m. (a, b) is the smallest positive integer divisible by both a and b.
The greatest common divisor can be computed by Euclid's algorithm. It consists of the following chain of equations.
a = bqt + r, , 0 < r, < b ,
b - ri <?2 + r2 » 0 < r2 < r, ,
ri = r2<h + r3 » 0 < r3 < r2 ,
rk-2 = rk-1qk + rk, 0<rk<rk-i, rk-l — fklk+l ■
Termination is guaranteed because the remainders rt form a strictly decreasing sequence. It is immediate from the chain that rk is a common divisor of a and b and, moreover, that any common divisor of a and b divides rk. Hence, rk = (a, b).
We estimate now the time complexity of the algorithm. It is easy to see that the ordinary division algorithm runs in quadratic time. We could still have altogether exponential time complexity if we would have only ri+l < rt. Fortunately, it is easy to see that r, + 2 < r,/2 holds for all i. This gives the upper bound 21og2a for the number of equations. Thus, the time complexity is altogether at most cubic.
Reading the chain of equations bottom up we find, altogether in cubic time, integers x and y such that
(a, b) = xa + yb .
Two integers a and b are relatively prime iff (a, b) = 1. The Euler phi-function <p(n), n > 1, is defined to be the number of nonnegative integers a < n such that a and n are relatively prime. It follows that <p( 1) = 1 and <p(pb) = pb — pb~\ where p is prime and b > 1. It is also easy to see that <p(mn) = (p(m)<p(n) if m and n are relatively prime. By these facts <p(n) can be computed for any n. The computation will be easy if the factorization of n is known.
We say that a is congruent to b modulo m, written
a = b (mod m)
iff m divides the difference a — b. The number m is called the modulus. We assume that m > 2. For every integer x, exactly one of the integers 0,1,..., m — 1 is congruent to x modulo m. This particular integer is called the least nonnegative remainder of x modulo m and denoted by
(x, mod m).
This notation appears frequently in this book in different contexts. Denote further by [x] the integer part of x, that is, the greatest integer < x. It follows that
(x, mod m) = x — [x/m] • m .
We have seen that if a and m are relatively prime, then there are integers x and y such that 1 = xa + ym. Hence, xa = 1 (mod m). The integer x is referred to as the inverse of a modulo m and denoted by a-1 (modm). The inverse is unique when congruent integers are considered to be equal. The time complexity of finding the inverse is roughly the same as that of Euclid's algorithm. This implies that also the congruence
az = b (mod m), (a, m) = 1 ,
can be solved in cubic time. To find z, one first computes a"'(modm) and multiplies it by b.
If (a, m) = 1 then, according to Euler's Theorem,
a"(m)= 1 (mod m).
If m is a prime not dividing a, this result takes the form
am~1 = 1 (mod m)
and is referred to as Fermat's Little Theorem.
If the moduli mi are pairwise relatively prime then the system of congruences
x = at (mod mt), i= 1,. . ., k ,
possesses a solution x unique up to congruence modulo M = m,.. . mk. This result, known as the Chinese Remainder Theorem, is established in Section 6.3.
A field F is a set together with the operations of addition and multiplication that satisfy the familiar requirements: associativity, commutativity, distributive
law, existence of an additive identity 0 and a multiplicative identity 1, additive inverses and multiplicative inverses for all elements except 0. Both the rational numbers and the real numbers constitute a field.
Finite fields F(q) with q elements are important in cryptography. It is easy to see that always q = p\ for some prime p and h > 1. A convenient way of representing the elements of F(q) is discussed in Section 3.5.
Denote by F*(q) the set of nonzero elements of F(q). An element g of F*(q) is termed a generator of F*(q) iff, for every a in F*{q), there is an integer x such that gx = a holds in F*(q). There are altogether <p(q — 1) generators g. The integer x is referred to as the discrete logarithm of a to the base g. It is known that the computing of discrete logarithms (when g, a and q are known) is roughly as hard as factorization.
Consider a prime p > 2. If an element a of F*(p) is a square, that is a = x2 for some x, a is called a quadratic residue modulo p. Otherwise, a is called a quadratic nonresidue modulo p. Clearly, a with 1 < a < p — 1 is a quadratic residue modulo p iff the congruence
x2 = a (mod p)
has a solution x. Then necessarily also — x is a solution, that is, a has two square roots modulo p. All quadratic residues are found by computing the squares of the elements 1,. . ., (p — l)/2. Thus, there are (p - l)/2 quadratic residues and non- residues.
The Legendre symbol for an integer a and prime p > 2 is defined by
0 if p divides a ,
1 if a is a quadratic residue modulo p , — 1 if a is a quadratic nonresidue modulo p .
Clearly, a can be replaced by any integer congruent to a (mod p) without changing the value of the Legendre symbol. The basic result concerning the Legendre symbol is
(*) = a(p~1)12 (modp).
\Pj
The Jacobi symbol is a generalization of the Legendre symbol. Consider an integer a and an odd number n > 2. Further, let n = pi'. . .p'kk be the prime factorization of n. Then the Jacobi symbol is defined to be the product of the corresponding Legendre symbols:
©-Gtf-GT
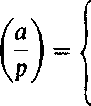
|
Clearly, also now a can be replaced by a number congruent to a (mod n) without changing the Jacobi symbol. The multiplicative property
follows easily from (*). Consequently,
For special values of a the Jacobi symbol can be computed as follows:
0 = (^r) = ("1)<""1,/2' d) = (-i)(n2-,)/8-
Basic reductions in the computation of the Jacobi symbol are carried out using the Law of Quadratic Reciprocity:
n)
where m and n are odd numbers greater than 2. Equivalently, un'ess
m = n = 3 (mod 4),
in which case I — | = — ( — \nj \m
The value of can now be computed, without factoring any numbers (apart
from taking out powers of 2) as follows. If necessary, m is replaced by (m, mod n); a similar replacement is made also at later stages of the procedure. The Law of
Quadratic Reciprocity is applied to reduce the "denominator" in As in case of
Euclid's algorithm, the reduction can be small in one reduction step, however, two consecutive steps reduce the denominator at least by a factor of 5. Altogether this
yields roughly the same time complexity estimate for computing ^ as we have
for Euclid's algorithm. An example of a computation is given in Section 6.5.
If p is prime, the described method constitutes also a fast algorithm for determining whether a is a quadratic residue or nonresidue modulo p. No such fast algorithm is known if, instead of a prime p, we are dealing with an arbitrary n. Let us consider in more detail the cryptographically important case, where n is the product of two odd primes, n = pq.
As we noticed above, half of the numbers 1,. .., p — 1 are quadratic residues modulo p, the other half being nonresidues. Of course the analogous statement holds for q. On the other hand, a number a is a quadratic residue modulo n, that is x2 = a (mod n) holds for some x, iff a is a quadratic residue both modulo p and modulo q. Altogether this means that exactly half of the numbers a with
0 < a < n and (a, n) = 1 satisfy (- j = + 1, and ( - j = — 1 holds for the other half. Moreover, half of the
= + 1 are quadratic residues modulo n, namely, those for

|
+ 1 .
are nonresidues. There seems to be no way of finding out which of the two cases occurs, unless one is able to factor n.
Assume that we know that a, 0 < a < n, is a quadratic residue modulo n. Hence, for some x,
x2 = a (mod n).
Finding x, that is, extracting square roots modulo n is a very important task in cryptography. Let us again consider the case n = pq. By our assumption, a is a quadratic residue both modulo p and modulo q. This implies the existence of numbers y and z such that
( + y)2 = a (mod p) and ( + z)2 = a (mod q).
Moreover, y and z can be found in polynomial time (where the degree of the polynomial is at most 4), provided that p and q are known. The details of such an algorithm are given, for instance, in [Ko]. It is assumed in the algorithm that a nonresidue modulo p is known, as well as a nonresidue modulo q. However, such nonresidues can be found fast by a stochastic algorithm.
From the congruences
x = ± y (mod p) and x = ± z (mod q)
we now get, by the Chinese Remainder Theorem, four square roots x of a modulo n. The square roots can be expressed as + u and + w, where u ^ ± w(mod«). Such u and w are referred to as different square roots. The following two facts are important in cryptography. The knowledge of two different square roots enables one to factor n. In fact
u2 — w2 = (u + w)(u — w) = 0 (mod n).
This means that n divides (u + w)(u — w). However, by the choice of u and w, n divides neither u + w nor u — w. This implies that the greatest common divisor of u + w and n (obtained quickly by Euclid's algorithm) is either p or q.

|
| numbers a satisfying which |
| The other half, namely, those for which |
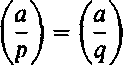
|
| - 1 |
The second important fact is that, whenever p = q = 3 (mod 4), then two different square roots u and w of the same number a modulo n possess different Jacobi symbols:

|
This follows because, as seen above, either
u = w(mod p) and u = — w(mod q)
or else
u = — w (mod p) and u = w (mod q), and by the assumption concerning p and q
1\
P ) \ 1
Problems
1. Encrypt the plaintext
DONOTGOTOSAUNASOONAFTEREATING
using KEYWORD-CAESAR with the keyword SUPERDOG and number 9.
2. The plaintext SAUNA is encrypted as TAKE BACK VAT OR BONDS. Describe the cryptosystem used.
3. The plaintext SAUNAANDLIFE is encrypted as RMEMHCZZT- CEZTZKKDA. Describe the cryptosystem used.
4. Encrypt according to Hill's cryptosystem (see Example 1.2) the plaintext PAYMOREMONEY when the matrix used is
|
| 17 17 5\ 21 18 21 2 2 19 y |
5. The matrix is now

|
| 11 2 19\ 5 23 25 . 20 7 1 , |
Encrypt STOPPAYMENTX.
6. Establish a necessary and sufficient condition for a matrix M to be invertible when arithmetic is carried out modulo 26. (This is required in Hill's cryptosystem.) Find the inverses of a few 2-dimensional matrices.
7. Hill's cryptosystem with a 2-dimensional matrix is used. The most frequent digrams in the cryptotext are RH and NI, whereas they are TH and HE in the plaintext language. What matrix can be computed from this information?
(2 3\
8. To encrypt one uses first the matrix I I and to the resulting text the
matrix ^^ ^ • Construct a single matrix with the same effect.
9. As Problem 8 but now the matrices are (in this order)
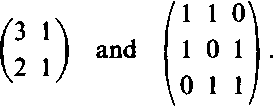
|
10. In general, if the original matrices are m- and n-dimensional, how big a matrix suffices for the combined effect?
11. A cryptosystem is closed under composition iff, for every two encryption keys, there is a single encryption key having the effect of the two keys applied consecutively. Closure under composition means that the consecutive application of two keys does not add security. The preceding problems show that Hill's cryptosystem is closed under composition. Study this property with respect to some cryptosystems discussed in this book.
12. In simple cryptosystems every encryption key can be represented as a composition of a few generator keys. In CAESAR such a generator is £,, the key mapping every letter to the next one. The affine system maps a letter x, 0 < x < 25, into the letter (ax + b, mod 26), where (a, 26) = 1. Show that no single key can be a generator for the affine system, whereas two keys suffice.
13. Decrypt the following cryptotext given to the participants of EUROCRYPT- 88 in Davos:
EXVITL AMSYMX EAKSSI KIRZMS YEKDAV OSINAL PVITHE R R J ML O OIEUSM GPLKSM ADAVOS LULRVK S I XMT A I DAVOS
14. Which city with four letters is in encrypted form BHFLYPBT when the following encryption method is used. First an arbitrary garbage letter is added after each plaintext letter. (Thus, in the resulting word the 2nd, 4th, 6th and 8th letters are insignificant.) Then Hill's system with a 2-dimensional matrix encrypting the wor'd AIDS into the word AIDS is used.
15. The plaintext alphabet is {A, B, C, D}. The monoalphabetic system is used, where the individual letters are encrypted as follows:
A BB , B AAB , C -> BAB , D A .
For instance, the word ABDA is encrypted as BBAABABB. Show that decryption is always unique. Show that it is not unique if the individual letters are encrypted:
A - AB , B BA , C->A, D->C.
16. The complement ~ x of a bit x is defined in the natural way: ~ 0 = 1 and
~ 1 = 0. Prove that if in DES every bit in the plaintext and in the key is replaced by its complement, then also in the cryptotext every bit will change to its complement.
17. Any word over the alphabet {A, B} can appear as plaintext. The first mono- alphabetic encryption key is defined by
A-►CCD, B -> C
and the second by
A-C, B -* DCC .
Which words over {A, B} are encrypted as the same word over {C, D} according to both keys?
18. The most frequent trigrams in the cryptotext are LME, WRI and ZYC, whereas they are THE, AND and THA in the plaintext language. What is the matrix used in Hill's cryptosystem?
19. Each letter x, 0 < x < 25, is encrypted as (/(x), mod 26), where/(x) is a quadratic polynomial. Compute the polynomial when the three most frequent letters in the cryptotext are Z, V, B (in this order), whereas they are E, T, N in the plaintext language.
20. Consider the very weak variant of ONE-TIME PAD discussed at the end of Section 1.3. However, now the basic book is this book. For instance, the key 12345 means the fifth letter of the fourth word in the third paragraph of Section 1.2. Encrypt the plaintext RACCOONDOGANDSAUNA using the key 43333.
21. Both the keyword and plaintext can be read in different ways from the Vigenere and Beaufort squares. Write arithmetical expressions for some of the mappings obtained.
22. A simple cryptosystem can be based on permutations as follows. The plaintext is divided into blocks of n characters each. A fixed permutation on the numbers {1,...,«} is applied to each block. For instance, SAUNA becomes UNSAA if n = 5, the permutation interchanges the first and third as well as the second and fourth letters but leaves the fifth letter unchanged. Show that the same effect can always be reached by a suitable Hill's cryptosystem.
23. A cryptosystem induces a language theoretic mapping from the set of plaintext words to the set of cryptotext words. In general, only little is known about such mappings but, for instance, the mapping induced by CAESAR is easy to characterize. Consider various cryptosystems and answer the question: is the induced mapping length preserving?
24. Give necessary and/or sufficient conditions for a mapping to be realizable by a PLAYFAIR square. The results enable you to construct "meaningful translations" such as the one presented in the text.
25. Explain the differences (apart from different alphabet sizes) between mappings realizable by a PLAYFAIR square and a 3 x 9 PLAYFAIR rectangle.
26. Same as Problem 24 but now for the Jefferson wheel. Observe especially the importance of the distance between the plaintext and cryptotext rows.
27. What is the period obtained from the lug matrix and step figure presented in the text?
28. Construct a lug matrix and a step figure giving rise to the period 17 (resp. 19-21).
29. Construct a lug matrix and a step figure giving rise to the maximal period. ([BeP] may be consulted.)
30. Show that the 10-tuple A' studied in Section 2.1 is injective, that is, there is no a such that the knapsack problem (A', a) would have two solutions.
31. Let A = (a,,. . ., a„) be a knapsack vector, that is, the a,'s are distinct positive integers. A positive integer a is represented by A iff a can be expressed as a sum of the fl,'s, where no a, appears twice. If A is injective, then clearly 2" - 1 integers are represented by A. This is the greatest possible number. What is the least possible number in terms of n?
32. Given a knapsack problem (A, k), you have to find all solutions. Show that this problem is not even in NP.
33. Why is 2047 a bad choice for the modulus in RSA, apart from its being too small?
34. Show that encryption and decryption exponents must coincide if 35 is the modulus in RSA.
35. Some plaintext blocks remain unchanged when encrypted according to RSA. Show that their number is
(1 + (e - l,p - 1))(1 + (<? - 1)(<? - 1)).
36. Construct examples of Shamir's algorithm, where at least two disjoint intervals for u/m are found. Can you say something general about the number of disjoint intervals? Is it possible that an interval reduces to a point?
37. Prove that the vector (/, i — 1, i — 2,. .., i — j), i — j > 1, is super-reachable exactly in case if both j = 2 and i > 4.
38. The vector (7, 3, 2) is ((7,15, 38), 73,84)-super-reachable. Apply the technique of Lemma 3.5 to get a small enough multiplier.
39. Prove that every injective (bl,b2,b3) is permutation-super-reachable.
40. Describe an algorithm for finding the smallest modulus m such that a given super-reachable vector is (A, t, m)-super-reachable.
41. Consider all knapsack vectors whose components are < 4. Prove that exactly the following ones are super-reachable:
(2,4,3), (4,3,2), (1,2,4), (2,4,1), (4,1,2).
42. Prove that (5, 3,4) and (5,4, 3) are the only super-reachable ones among vectors with components 3,4, 5.
43. Represent the elements of F(27) in terms of the root of a polynomial irreducible over F(3). Find a generator and compute the table of logarithms.
44. Study the cryptanalysis of the cryptosystem based on dense knapsacks, when some of the trapdoor items are known. (Here [Cho] should be consulted.)
45. Consider the first illustration (n = 55) in Example 4.1. Send a signed message to a user whose public encryption exponent is 13. (You have e = 7, d = 23.)
46. Show that the number 3215031751 is composite and a strong pseudoprime to each of the bases 2, 3, 5, 7.
47. Consider the general method for key exchange presented at the very end of Chapter 4 in case of some specific function f. Can you improve the ratio m/m2 between the work done by the legal user and the work done by the cryptanalyst?
48. Assume that you have an algorithm for computing one of SQUAREFREE- NESS (n) (see Section 2.2) and <p(n). Can you reduce this to an algorithm for computing the other?
49. The initial value is 3 in .a functional cryptosystem, the functions being /0(x) = 3x and/t(x) = 3x 4- 1. Thus, Oil is encrypted as
3/o/i/i = 85.
What is a very simple way to decrypt a cryptotext written as a decimal number? Which numbers can appear as cryptotexts?
50. Show that the knapsack vector
(2106, 880, 1320,974, 2388,1617, 1568,2523, 48, 897) is super-reachable.
51. Give an example of a knapsack problem (A{i), a(i')) having exactly i solutions. i= 1,2,... .
52. Analogously to Example 3.5, let the publicized items be A = (1, 2, 3,0, 0,4) (A is viewed as a column vector) and m = 7. The secret matrix is
(I 0 1 0 0 l\ H = 0 1 1 1 0 1 .
\l 0 1 1 1 oy
What is the signature for the plaintext 3 (i) by the direct method, (ii) using the randomizing vector (1,0,0,0,1,1)?
53. It is clear that a dual theory can be based on decreasing and super-decreasing vectors, defined in the same way as increasing and super-increasing vectors. In particular, the notion of super-d-reachability refers to super-decreasing vectors. Give examples of injective vectors that are neither super-reachable nor super-J-reachable.
54. Construct a protocol for throwing a dice by telephone. Be not satisfied with the following obvious solution. Flip a coin three times. If the outcome is heads-heads-heads or tails-tails-tails, repeat the procedure until some other outcome is obtained.
55. Assume that the primes p and q in RSA have 100 digits, the first digit being / 0. Estimate the number of possibilities for n.
56. YJCVKUVJGJGCTVQHUCWPC? UVQXG.
57. Prove that the remainders in Euclid's algorithm satisfy the inequality rj + 2 <Tjl2, for all j. Construct a variant of the algorithm, by allowing negative remainders, where a slightly better convergence rJ+2 < rj+ J2 is obtained.
58. Decrypt
KOKOOKOKOONKOKOKOKKOKOKOKOKKOKOKOKOKOKKO and
& ^ Xlj tft
Both are actually statements or conversations in a wellknown natural language. Certainly the plaintext language is of some importance!
59. Consider the plaintext of length 47, discussed in connection with the C-36 encryption. If YES is added to the end of the plaintext, how does the cryptotext continue?
60. Assume that (a, m) = 1. Show that a'"{m>'2 = 1 (modm), provided m is not one of the numbers 1, 2,4, pk and 2pk, where p is an odd prime and k > 1.
61. Prove that (am - 1, a" - 1) = aim-n) - 1. It is assumed that a > 1.
62. There are always in RSA encryption exponents such that every plaintext is encrypted as itself. More explicitly, prove the following assertion. For every choice of p and q, e can be chosen in such a way that we = w(mod n) holds for all w. (The trivial choices e = 1 and e = <p(n) + 1 are not allowed.)
63. The following encryption method is classical and was illustrated in Fig. 2.4. A large prime p is known to all users. Each user chooses and keeps secret encryption and decryption exponents e and d such that ed = l(modp — 1). Thus, A encrypts a plaintext w by
Ea(w) = (we\ mod p) .
First A sends the cryptotext EA{w) = cXoB.B responds by sending EB(c) = ct to A. Finally, A sends DA(c1) to B. Show that B is able to decrypt and discuss the security issues involved.
64. Give necessary and sufficient conditions for p and t to the effect that every element # 0,1 in the field F(p') is (i) a generator, (ii) the square of a generator.
65. Assume that the encryption exponent e in RSA is small. Assume that an oracle always tells you £(x + r), given £(x) and r. (Clearly, no oracle is needed to tell E{xr), given E{x) and r.) How are you able to decrypt?
66. Factor n = 4386607 given <p(n) = 4382136.
67. Consider the modification of RSA, where the modulus n is the product of three large primes p, q and r. Also now ed = 1 (mod cp(n)) holds for encryption and decryption exponents. Discuss the advantages and disadvantages of the modification in comparison with the ordinary RSA.
68. Let /(x) and g(x) be one-way functions. Give a heuristic argument to show that none of the functions /(x) + g(x), f(x)-g(x) and f(g(x)) is necessarily one-way.
69. Show that the following problem is in the intersection of NP and Co-NP for every public-key cryptosystem. Given a cryptotext, you have to decide whether or not SUVI appears as a subword in the corresponding plaintext.
70. Consider the last illustration in Example 4.2., where n = 8137. Compute the table for r(i), ANS(i) and t(i) when x = 20. Read the remarks at the end of the example.
71. In DES each S-box translates a 6-bit input into a 4-bit output. Prove that always changing one input bit results in changing at least two output bits.
72. When you fix two input bits, each S-box defines a mapping of 4-bit sequences into 4-bit sequences. Which bits have to be fixed in order to get a bijection in all eight cases? Give an example of a mapping that is not a bijection.
73. Prove that there are infinitely many pairs of primes (p, q) such that p = q = 3 (mod 4) but p ^ q (mod 8). Use Dirichlet's Theorem to the effect that there are infinitely many primes in the sequence ia + b, i = 1,2,..., provided a and b are positive integers with (a, b) = 1.
74. Consider the knapsack vector A =(u„..., a„), where a, = P/ph i = 1,. . ., n, and pf are distinct primes whose product is P. Give a simple algorithm for solving the knapsack problem (A, a).
| 75. 76. 77. 78. 79. 80. 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. |
Design a cryptosystem of Williams for the basic choice p = 47, q = 59 often discussed in the text. Encrypt 1991. See Section 5.1. Assume that in RSA we have p = 127 and q = 131. How many messages are encrypted into themselves by both of the encryption exponents 29 and 31? Consider the Diffie-Hellman key exchange system (Section 4.6) with q = 4079 and g = 1709 and secret numbers /c, = 2344 and k2 = 3420. What numbers are publicized and what is the common key shared by the users Ax and A2? Find all square roots of 64 modulo 105.
In the El Gamal scheme discussed at the end of Section 4.6 a prime q and a generator g of F*(q) are publicized. What is the effect on encryption and decryption if, in fact, g is not a generator?
The hexadecimal representation of 4-bit sequences 0000, 0001, ...,1111 uses the characters 0, 1, 2,. . ., 9, A, B, C, D, E, F, in the order indicated. Assume that the DES key is 0123456789ABCDEF. Encrypt the plaintexts 516 and 616. Study the cryptographic significance of the initial permutation in DES. List all quadratic residues modulo 29 and those modulo 31. Prove that, for an odd prime p, — 3 is a quadratic residue modulo p iff p = 1 (mod 3). Let n be as in RSA. Prove that the problem of listing all quadratic residues modulo n is not even in NP.
Consider the identification scheme as in Example 6.5 but now n = 2491. P's secret identification consists of the triple
Cj = 143 , c2 = 32 , c3 = 2261 .
Describe one round of the protocol, where the further choices r = 61 and S = {1, 3} are made. Prove Lemma 5.1.
Consider the system based on iterated morphisms, where the underlying morphisms are
h0 : a ac , b -> ba , c -»ca , h1:a-*aa, b->bc, c^cb,
the initial word being c. Show that the legal receiver can decrypt as follows. First the interpretation morphism is applied to the cryptotext to get a word w over the alphabet {a, b, c}. A word u is constructed such that the i-th letter of u is the (2'~1 + l)th letter of w. The word u is read from right to left, and a and b are replaced by 0 and 1, respectively, (u will contain no c's.) Show that finding a trapdoor pair for the cryptosystem based on iterated morphisms is an /VP-complete problem. Consult [Kar3]. Give reasons why decoding is essentially simpler for Goppa codes than for linear codes.
Consider the protocol for playing poker by phone, discussed at the end of Section 6.2. What are the possibilities for cheating if some of the chosen numbers p, and qt are actually not primes. (See the discussion about flipping a coin by telephone.)
Devise a method for sharing a secret, based on some other idea than the Chinese Remainder Theorem.
91. Devise a voting protocol as in Section 6.4 for the case, where there are two superpowers and five ordinary powers.
92. A possesses 8 secrets and wants to transfer exactly one of them to B in such a way that only B knows which of the secrets was transferred. However, B cannot choose which secret he wants. Devise a protocol.
93. Give an explicit numerical example of the 7-step protocol described after Example 6.3. Discuss the possibilities of active cheating in your protocol.
94. Describe explicitly a protocol discussed in Section 6.6 for thirteen voters and two voting Strategies (i) with two agencies C and L, (ii) with only one agency C.
95. Devise a protocol for proving in a zero-knowledge manner that you know a solution to a given knapsack problem. Preferably use the idea of lockable boxes.
96. Consider the travelling salesperson problem in the form that, given a map indicating all the distances and a number k, you have to find a route through all cities on the map with length < k. Devise a zero-knowledge protocol for convincing a verifier that you know a solution.
97. Consider some axiom system for the propositional calculus and a simple theorem whose proof consists of, say, five steps. Devise a zero-knowledge proof for the theorem. Discuss whether or not your ideas carry over to any proof in any formal system.
98. Use RSA to obtain a method for constructing lockable boxes.
99. Consider the wffpc (xt v ~ x2 v x3) a (x2 v x3) a ( ~ x, v x3) a ~ x3. Explain why you get caught if you try to prove in a zero-knowledge manner that you know a satisfiability assignment.
100. Give a numerical example of the second protocol presented in Section 6.9 in its full form where A is a matrix. Consult [Sh5] for generalizations of the protocol and study the security issues involved.
Date: 2015-02-16; view: 1324
| <== previous page | | | next page ==> |
| Appendix A. Tutorial in Complexity Theory | | | Historical and Bibliographical Remarks |