
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Convincing Proofs with No Details
In the next three sections we focus the attention on the following challenging and fascinating problem. Assume that P ("the Prover", Peter) knows some information. It could be a proof of long-standing conjecture (such as Fermat's Last Theorem), the prime factorization of a large integer, a 3-coloring of a graph, a password or an identification number. The essential thing is that P's information is verifiable: there is an effective procedure for checking its validity. In connection with a mathematical theorem this implies that the proof is given in some formal system, where every step of the proof can be validated. P would like to convince V ("the Verifier", Vera), beyond any reasonable doubt, that he is in the possession of this information.
P could simply disclose this information so that V could do the checking herself. If the information consists of the prime factors p and q of a large integer n, P could tell V the numbers p and q, and V could convince herself that n = pq. This is a maximum disclosure proof, where V actually learns the information and can later on show it to someone else and even claim that she factored n herself.
In a minimum disclosure proof P convinces V that he has the information, but this happens in a way that does not reveal a bit of the information and, consequently, does not in any way help V to determine the information. V is almost sure (because the probability of P cheating can be made arbitrarily small) that P has the information, say, the two factors of n. But V has no idea about the factors themselves and cannot tell anything about them to a third party.
A very simple minimum disclosure proof about the knowledge of the factors of n is the following.
Step I: V chooses a random integer x and tells (x4, mod n) to P. Step 2: P tells (x2, mod n) to V.
V obtains no information new to her because she can square x herself. On the other hand, we know that extracting square roots is equivalent to factoring n. In Step 2, P not only has to extract a square root of x4 but the particular one among the four square roots that is a quadratic residue (mod n). Determining quadratic residuosity is also intractable without knowing the factors of n. Of course, the possibility of P succeeding without knowing the factors of n can be made still smaller by iterating the protocol.
Let us repeat our basic requirements. We assume that the information is the proof of a theorem.
(I) The Prover probably cannot cheat the Verifier. If the Prover does not know a proof of the theorem, his chances of convincing the verifier that he knows a proof are negligible.
(II) The Verifier cannot cheat the Prover. She gets not a slightest hint of the proof, apart from the fact that the Prover knows a proof. In particular, the Verifier cannot prove the theorem to anyone else without proving it herself from scratch.
Protocols satisfying (I) and (II) contradict the common belief that one necessarily gains additional insight into a theorem by getting convinced that it holds. Minimum disclosure proofs yield no such insight. Whatever one can learn from the proof, one can learn from the statement of the theorem.
Minimum disclosure proofs are conceivable even if the Prover has no definite proof to start with but only an argument very likely to be true. For instance, P might have found the numbers p and q by one of the primality tests of Section 4.3 and is quite convinced that n = pq is the prime factorization, although it is possible that p or q can be decomposed further. P can transfer his conviction to V in a minimum disclosure manner, which implies that V is unable to convince a third party.
The protocol above was constructed in an ad hoc manner, based on the special interconnection between factoring and extracting square roots. Some general ideas are needed if one wants to construct protocols satisfying (I) and (II) for a large class, such as problems in NP. The crucial idea in the construction will be that of a lockable box. The Verifier cannot open it because the Prover has the key. On the other hand, the Prover has to commit himself to the contents of the box, that is, he cannot change the contents when he opens the box. In fact, the Verifier may watch when the Prover opens the box.
For the moment being we do not discuss how the boxes are constructed but will return later in this section to this issue. Basically, the hardware consisting of boxes can be replaced by public-key cryptography. Locking information in a box means applying a one-way function to it. The Prover knows the inverse function and applies it when opening the box. His commitment to the box can be verified by applying the one-way function to the plaintext information.
Certain assumptions have to be made because public-key cryptography is used. If the boxes are constructed using RSA or discrete logarithms, intractability of factoring or taking discrete logarithms is assumed. In most cases it is possible to change the underlying public-key cryptosystem, so it suffices to assume the existence of a one-way function.
Boxes are used in the following minimum disclosure proof of the 3-colorability of a graph. A 3-coloring of a graph consists of providing the nodes with the colors B (blue), R (red) and W(white) in such a way that no two adjacent (that is, connected by an edge) nodes get the same color. 3-colorability is known to be an NP-complete problem.
P wants to convince V that he knows a 3-coloring of a graph G with t nodes 1,. . ., t. The protocol has k rounds. Each round consists of 4 steps and proceeds as follows.
Step 1: P prepares and presents to Kthe following locked boxes Bt, Bf, 1 < i < 3t, and Bt j, 1 <i <j < It. Each of the boxes Bi contains one of the nodes, and each of the boxes Bf one of the colors in such a way that, for every pair (ij, c), where 1 < ii < t and c = B,R, W, there is an i such that il is in B, and c is in Bf. Moreover, the pairs (/,, c) appear in the pairs of boxes (B„ Bf) in a random order.
Each of the boxes B, j contains either 0 or 1. 1 appears iff both of the following conditions are satisfied. If/j and f appear in the boxes Bt and Bp respectively, then there is an edge between /, and in G. Moreover, in the Prover's 3-coloring, the color assigned to (resp. ) appears in the box Bf (resp. Bj). The boxes B„ Bf and Bf j are referred to as node, color and edge boxes.
Step 2: V flips a coin and tells P the outcome.
Step 3: (a) If the outcome was "heads", P opens all node and edge boxes, (b) If the outcome was "tails", P opens all color boxes and such edge boxes Btthat the nodes contained in Bt and Bj are assigned the same color in P's 3-coloring.
Step 4: (a) V verfies that she got a copy of G and 21 isolated nodes. If so, she accepts, otherwise rejects. The verification is easy because the opened node boxes tell the proper node labels, so no problem concerning graph isomorphism has to be settled, (b) V verifies that all of the opened 3t(t — l)/2 edge boxes contain 0 and that each color appears t times in the color boxes. If so, she accepts, otherwise rejects.
The following facts are now obvious. The boxes have to be reconstructed for each round of the protocol. Otherwise, V learns everything in two rounds by choosing (a)- and (b)-lines. If the boxes are always reconstructed, V learns nothing about the coloring. If (a)-line is followed, she gets just a copy of G. If (b)-line is followed, she learns only that in P's 3-coloring of G no two adjacent nodes get the same color and, consequently, P's 3-coloring is a correct one. P always passes the test if he knows a 3-coloring of G. Otherwise, he may try to cheat in two ways, (i) He does not lock in the boxes a description of G but rather of some other graph whose 3-coloring he knows. Then he gets caught if (a)-line is followed, (ii) P uses a false 3-coloring. Then he gets caught if (b)-line is followed. Thus, the probability of a false prover passing k rounds is 2~\ and we have established the following result.
Theorem 6.2. The given protocol for 3-coloring satisfies conditions (I) and (II). As regards (I), the probability of the Prover cheating is 2~\ where k is the number of rounds in the protocol.
| 2 ,B |
| 4 ,R |
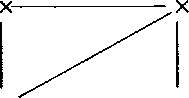
Example 6.4. Assume that t = 4, the graph G being depicted below. P knows the following 3-coloring.
1 ,W
|
| x- |
| x |
3 ,W
P prepares the following node and color boxes.
J5, : 2 Bi : W
B2 : 1 Bc2 : R
B3 : 1 B% : W
| B4 : | 4 | B% : | B |
| Bs : | 2 | Bc5: | R |
| B6 : | 4 | B% : | W |
| B7 : | 3 | Bj : | B |
| Bs : | 3 | Bca : | R |
| Bg : | 4 | B% : | R |
| B io: | B io: | B | |
| Bn: | B\ i: | B | |
| B12: | BI2. | W |
Moreover, P prepares 66 edge boxes B:,j such that the 5 boxes 11' B3g, Bgii, Bg l2, B Uil2
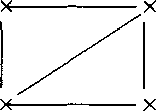
contain 1, and the remaining 61 boxes contain 0. If (a)-line is followed, V gets the graph
3 11 1 2 4 5
 9 12
9 12
|
where we use the indices of the node boxes as labels. The opened node boxes tell V that the labels 3, 11, 12, 9 are, in this order 1, 2, 3, 4. So V gets the original G without colors and 8 isolated nodes.
If (b)-line is followed, the 18 edge boxes opened for V are:
| Bi, 3' | Bu | 6' | B1. 12' | B2,5> B2 8, B2 9, |
| B3,6> | b3. | 12' | B4. 7' | •®4, 10' ^4, 11' B 5g, |
| B5,9' | Be, | 12' | B~if 10' | B7,ii' Bs g, Bio n |
All of these boxes contain 0, as they should. □
The following protocol is different in the sense that lockable boxes are not used, although they are present implicitly. P wants to convince V that he knows an isomorphism g between two given graphs G, and G2. (By definition, an isomorphism between G, and G2 is a 1-to-l mapping n of the nodes of Gl onto the nodes of G2 that is also edge-invariant: any nodes x and y are adjacent in G, iff rr(x) and n(y) are adjacent in G2.) The protocol consists of k rounds of the following three steps.
Step 1: P generates and tells V a random isomorphic copy G, of G,.
Step 2: V asks P to tell her an isomorphism between G„ and G^, where she has chosen /? from the indices 1 and 2.
Step 3: P acts as requested.
If P knows an isomorphism between Gl and G2, Step 3 will always be easy for him because he knows also the inverse of the isomorphism of G, onto Ga. Otherwise, P is in trouble if (I = 2. One might think that the Verifier learns something if, for instance, Ga = G2 and p = 1. The point is that Kdoes not get any information she could not have obtained without the Prover: she could have hit such a fortunate random copy Ga herself!
The problem of graph non-isomorphism is in Co-NP but it is not known whether it is in NP. Of course, it is in P-SPACE. Using the following simple protocol, P can convince V that he knows that the graphs G0 and G, are not isomorphic.
Step 1: V generates a random sequences of bits i,,..., ik and random graphs Hh,..., Hik such that always Htj is isomorphic to Gir V tells P the sequence of graphs Htj.
Step 2: P tells V the sequence of bits i,, . . . ,ik.
Clearly, P has no way of knowing the sequence of bits if the original graphs G0 and G, are isomorphic. In this case, the probability of P getting caught in Step 2 equals 1 — 2~k. If G0 and G{ are not isomorphic and P has enough computing power to settle the problem of graph isomorphism, V will be convinced.
According to a very recent result of A. Shamir, P-SPACE is the collection of problems possessing such an interactive proof. More specifically, P has unlimited computing power but V works in polynomial time and has to become convinced with arbitrarily high probability. The result is particularly interesting because a proposed solution for a problem in P-SPACE cannot necessarily be checked in polynomial time. Thus, interaction constitutes here the missing link.
Let us now discuss a possible way of constructing lockable boxes. It is no loss of generality to assume that each box contains only one bit. If it is originally supposed to contain more information, it can be replaced by several boxes that are opened simultaneously. The method described below is based on the assumption that the computation of discrete logarithms (mod p) is intractable.
First a large prime p and a generator g of F*(p) are publicized. This means either that P and V agree about p and g or, more generally, that p and g can be used by all parties wishing to engage in minimum disclosure proofs. If there is any doubt of p and g actually being a prime and a generator, we may assume that also the factorization of p — 1 is known, whence the facts concerning p and g can be immediately verified.
At the beginning V chooses and tells P a random number r, 1 < r < p — 1. P cannot compute the discrete logarithm of r (mod p), that is, an integer e such that g' = r (mod p). This follows by our assumption concerning the intractability of
computing discrete logarithms (which is not essentially simpler even if the factorization of p — 1 is known).
In order to lock a bit b into a box, P chooses a number y randomly and secretly and tells Kthe "box": x = (rbg", mod p). Clearly, any element of F *(p) is of the form (ig", mod p), as well as of the form (rgy, mod p). This implies that x does not reveal anything of the locked bit b. When P wants to open the box for V, he tells V the "key", that is, y. This does not help V in any way to open other boxes.
On the other hand, this method forces P to commit himself to the bit b. He cannot open the box both as 0 and 1. Suppose the contrary: P can choose two numbers y and y' such that
(,gy, mod p) = (rgy, mod p),
and then later announce y or / as the key to the box, depending on whether he wants 0 or 1 to appear in the box. But now
r = g" (mod p)
and, consequently, P is able to compute the discrete logarithm of r, which contradicts our assumption. This means that, when locking the bit b into the box, P has committed himself to b and cannot later change b.
Date: 2015-02-16; view: 1361
| <== previous page | | | next page ==> |
| Applications: Banking and Ballots | | | Zero-Knowledge Proofs |