Oblivious Transfer

We now consider another variant of confidential communication. A party A pos­sessing a secret wants to transfer the secret to another party B in such a way that, after the protocol, A does not know whether B got the secret but B knows it. The probability for such an oblivious transfer being successful could be, for instance, 50%.

A modified version of oblivious transfer is that A possesses several secrets. She wants to transfer one of them to B in such a way that only B knows which of the secrets was transferred.

There are numerous situations where the need for such oblivious transfers might occur. A could be a seller of secrets who has listed a number of questions and offers to sell the answer to any of them at a huge price which we assume to be the same for each of the secrets. The secrets could be of political importance, for instance, concerning the whereabouts of a sought-after person. B wants to buy a secret but does not want to disclose which one. For instance, B might be an agent of a superpower. Disclosing the ignorance of the superpower concerning a specific matter might be delicate or even dangerous.

It should be emphasized that all constraints involved in partial disclosure of secrets and oblivious transfer can be easily met with the help of an additional party, namely, a trusted referee. All information is given to the referee who distributes it to the communicating parties according to the constraints. The importance of the protocols lies in the fact that the trusted referee becomes unnecessary. This is the basic issue why protocols based on public-key cryptography open new vistas for communication. In many cases it is impossible to find a referee trusted by all parties. Who would be a referee trusted by the superpowers?

Consider first the case where A wants to transfer obliviously a secret to B. We assume that the secret is the factorization of the product n of two large primes. In fact, this is no loss of generality because the secret can be anything encrypted using an RSA cryptosystem. Then the knowledge of the factorization opens the secret.

The following protocol is rather simple and is based on the fact met before (for instance, in Section 6.2) that the knowledge of two different square roots (mod n) of the same number enables one to factor n.

Step 1: B chooses a number x and tells the number (x², mod n) to A.

Step 2: A (who knows the factorization n = pq) computes the four square roots + x, + y of x² (mod n) and tells one of them to B. (Observe that A knows only the square and, thus, she has no way of knowing which of the square roots is x.)

Step 3: B checks whether the square root he got in Step 2 is congruent to + x (mod n). If this is the case, B got no new information. Otherwise, B has two different square roots of the same number (mod n) and, hence, is able to factor n. A has no way of knowing whether or not this is the case.

Obviously, the probability of A hitting a square root correct from B's point of view equals 1/2.

We now present another protocol for oblivious transfer. The setup is more general than before. A has two secrets s₀ and S;. She transfers one of them to B but does not know which one B got. The previous setup is obtained by letting be a triviality. Moreover, the new protocol is non-interactive: B sends nothing to A.

The transfer can be carried out between any two users A and B of some system. All users of the system know some large prime p, a generator g of F*{p) and a number c but nobody knows the discrete logarithm of c. In general, we assume that computing discrete logarithms is intractable: one cannot compute (g^xy, mod p) from (g^x, mod p) and (g^y, mod p). Since in the following discussion arithmetic is carried out modulo p, we write, for instance, g^x rather than (g^x, mod p).

A user, say B, computes his public encryption and secret decryption keys as follows. B picks randomly a bit i and a number x, 0 < x < p — 2, and computes

= and /?!_, = c(g^x)~' .

His public encryption key is now (/5₀, /?and his secret decryption key (i, x).

Since the discrete logarithm of c is unknown, B cannot know the discrete logarithms of both /J₀ and /?,. Moreover, the public encryption key does not reveal which of the two discrete logarithms B knows. Before sending B anything, A checks that his public encryption key is correctly formed: the equation /?₀^ = c should hold.

For bit sequences s, and s₂ of equal length, ^XORsj is the sequence obtained from s i and s₂ by bitwise addition (without carry). By adding O's to the beginning of the shorter sequence, the lengths of two bit sequences can always be made equal. XOR refers to exclusive or: bitwise addition amounts to exclusive disjunction when 0 and 1 are interpreted as truth values.

We are now ready for the non-interactive oblivious transfer of either s₀ or s,, assumed to be binary integers.

Step 1: A picks randomly y₀ and y_t from the interval [0, p — 2] and computes, for

j = 0, 1,

= 9^y\ yj = P]^J, rj = _SjXOR y;

She sends a₀, ar₀ and r_l to B.

Step 2: Using his secret decryption key, B computes

«f = 9^xyi = W = 7„ s, = y_fXOR r,.

We have met earlier passive and active eavesdroppers. In formal definitions and proofs concerning the security of protocols it is necessary to distinguish between passive and active cheaters. The former follow the protocol but try to obtain more information than actually intended. A typical example of a passive cheater is the poker player described in Section 6.1 who uses the fact that aces are quadratic residues. An active cheater may do anything and not follow the protocol at all. An example is a person using a false age in the age protocol. It is intuitively clear that there can be very little security in a protocol if most of the parties are active cheaters. On the other hand, a good protocol should exclude the possibility of passive cheating.

Let us now go back to oblivious transfers and investigate how A who possesses several secrets can transfer one of them to B in such a way that only B knows which of the secrets was transferred. Assume that we have to take care of passive cheating only.

Assume that s,,.. ., s_k are 4's secrets, where each s is a sequence of bits. Thus, A has publicized the secrets, for instance, as a list of questions, and the sequences s_} provide the answers. The protocol now runs as follows.

Step 1: A tells B a one-way function / but keeps f~¹ to herself.

Step 2: B has decided to buy the secret s,. He chooses k random values x_lt... ,x_k from /'s domain and tells A the fc-tuple (y_l5 . . . ,y_k), where

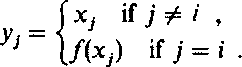
Step 3: A computes z_i = f ^l(y_J),j = 1,... ,k, and tells B the numbers ZyXORs,,

Step 4: B knows z, = /"¹ (/(*,-)) = x, and, hence, is able to compute s_f.

Observe that B has no information about Zj, for j # i, and consequently is not able to compute any Sj,j ^ i. A has no way of distinguishing the exceptional value y_t. This concerns passive cheating. Of course, if B is an active cheater and deviates from the protocol, he can learn more secrets by presenting several of the numbers yj in the form f(xj).

The above protocol uses an abstract one-way function f. Instead, we may assume that the secrets are encrypted using RSA, each secret by a different

RSA-system. Thus, disclosing a secret amounts to factoring the corresponding modulus. The protocol is based on the same idea as the poker protocol discussed in Section 6.2. Thus, A has publicized in advance a list telling what the k secrets are all about.

Step 1: A constructs k RSA-systems such that in each system the two primes Pj and qj are congruent to 3 (mod 4). (This guarantees that two different square roots modulo rij = p_}qj of the same number have different Jacobi symbols.) She tells B the encryption keys (e_p rij), j = 1,.. ., k, as well as the secrets in the encrypted form

(sJ^J, mod rij), j = 1,. . . , k .

Numerical encoding and eventual block division of the secrets have been agreed upon in advance.

Step 2: B chooses k numbers x_1;..., x_k, computes the Jacobi symbols ^ and

the squares (xf, mod nj),j=l,...,k.He tells A the squares and the correspond­ing Jacobi symbols, with the following exception. If B has chosen to buy the secret

s,-, he tells A the square (xf, mod n,) and the Jacobi symbol —

Step 3: In all k cases, A computes the square roots and tells B the square root whose Jacobi symbol she received in Step 2.

Step 4: B has now two different square roots of xf (mod n_;) and, consequently, is able to factor n„ find the decryption exponent d_t and the secret s_t. For indices j ^ i, B received no new information in Step 3 because he only got back the square root he already had.

A has no way of distinguishing the specific index i. Under the assumption of RSA being secure, the above remarks concerning passive cheaters are applicable also now. B can cheat actively in Step 2 by choosing several exceptional indices i.

Example 6.3. We refer to Example 4.1. Assume that A wants to transfer obliviously the factorization of n = 2773. Suppose B tells A the number 2562 in Step 1 of the protocol. A then computes the four square roots as follows. Since A knows the factors 47 and 59 of 2773, she computes the numbers

(2562, mod 47) = 24 and (2562, mod 59) = 25 .

The square roots of 24 modulo 47 are + 27. The square roots of 25 modulo 59 are + 5. Since the inverse of 59 (mod 47) equals 4 and the inverse of 47 (mod 59) equals 54, the Chinese Remainder Theorem yields ± 27 • 59 • 4 + 5 • 47 • 54 as the four square roots, or 349,772,2001 and 2424 after reduction (mod 2773). If B originally had 2001, he gets in Step 2 decisive new information if A returns 349 or 2424, whereas B gets nothing new if A returns 772 or 2001.

Assume next that A sells secrets, encrypted using RSA systems in the way explained in the last protocol above. Assume further that the modulus used in the encryption of some secret s is n = 2773 and that B has chosen in Step 2 the number 2001 and computed the square 2562. B is able to compute the Jacobi symbol without factoring:

/2001 \ _ /2773\ _ / T72 \ _ /_193\ _ /200l\ _ /J71_\ V2773/ ~ \ 2001 / ~ V²⁰⁰¹ / ~ V²⁰⁰¹ / V ¹⁹³ / \¹⁹³/

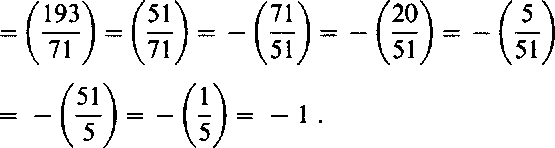
If B wants to buy s, he tells A the pair (2562,1) and gets back either 349 or 2424 in Step 3. Since 47 (but not 59) divides both 349 + 2001 and 2424 - 2001, B is able to factor n. If B does not want to buy s, he tells A the pair (2562, — 1) and obtains no new information in Step 3.

The following observation concerns the very simple RSA system with the modulus n = 55, discussed at the beginning of Example 4.1. Assume that B has chosen in Step 2 the number 2, for which (2/55) = 1. If B wants to buy the corresponding secret, he tells A the pair (4, — 1). He might then get back in Step 3 the number 53 which is nothing new for him. On the other hand, he might not want to buy the secret and tells A the pair (4,1) and still gets back in Step 3 the number 13 which enables him to factor n. The reason for these confusions is that one of the factors of n is not congruent to 3 modulo 4, as it should be according to the protocol. □

Let us go back to the secret selling of secrets, where we now assume that also active cheating is possible. Clearly, the situation cannot be under control if both A and B are active cheaters. (In all protocols like this one, it is customary to assume that at most half of the parties are active cheaters.) We assume that B is the eventual active cheater. To prevent active cheating, the protocol is basically modified as follows. B has to commit himself to a specific action, that is to specify which particular one of the secrets he wants to buy. The commitment may be "locked in a box" using a one-way function, but in the course of the protocol B has to convince A that he is acting according to the commitment. This he should do without disclosing any information about the action itself-a typical case of a minimum disclosure or zero-knowledge proof. The latter will be discussed in Sections 6.7 and 6.8. We now give the protocol in a very much simpler form that still makes active cheating highly improbable. We use the notion of flipping a number in the same sense as in Section 6.2. As before, s_t,. .., s_k are A's secrets.

Step 1: A flips to B k numbers x_t,... ,x_k. The number of bits in the x's has been agreed upon in advance. It may be assumed to coincide with the numbers of bits in the s's.

Step 2: A tells B a one-way function / but keeps the inverse / ¹ to herself.

Step 3: If B has decided to buy the secret s_t, he computes/(x,). Some bits in/(x,) coincide with the corresponding bits in x,. Let they be the bits in positions «,, . . . , u,, counted from the beginning.

Step 4: B tells A the bit in x_a in position u^, for all 1 < a < k and 1 < < t. He does this in such a way that A can verify the information. For instance, if the first coin flipping protocol from Section 6.2 has been followed, B tells in each case his original square root.

Step 5: B tells A the /c-tuple (y,, . . ., y_k), where

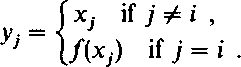
A verifies that the information is in accordance with Step 4.

Step 6: A tells B the number/"'(y^XOR s_p j = 1,. . ., k.

The above protocol is based on the fact that the number t in Step 3 is approximately half of the number of bits in x,. (It is assumed that / has a reason­ably random behavior.) If B would choose two exceptional y/s in Step 5, the number of "stable" bits would be too small because B has committed himself to the x's produced in Step 1 and also has to validate the commitment later on.

A may cheat by computing, for each j, the positions of the bits for which y_; and f~¹ (>j) coincide. For j = i, the positions are the ones communicated to A in Step 4, whereas for j # i the positions are different with an overwhelming probability.

A simple way to overcome this difficulty is to consider two buyers B and C. As before, A has the secrets s,,. .., s_k. The parties A, B, C do not form coalitions.

Step 1: A tells B and C individually one-way functions / and g but keeps the inverses to herself.

Step 2: B tells C (resp. C tells B) k random numbers x_t,. . ., x_k (resp. x\,..., x'_k). The numbers need not be flipped, and they have as many bits as the s's.

Step 3: B (resp. C) computes f(x'_b) (resp. <?(x_c)) for his chosen index b (resp c). The function and argument values are compared with respect to "fixed points", that is, bits remaining invariant in the transition from xj, to f{x'_h) (resp. from x_c to g(x_c)).

Step 4: B tells C (resp. C tells B) the indices of the fixed points. Call these indices stable for B (resp. for C).

Step 5: B (resp. C) tells A the numbers y_x,. .., y_k (resp. y\,.. ., y'_k), where the y's result from the x's by changing every bit, whose index is not stable for C (resp. for B), to its complement.

Step 6: A tells to B (resp. to C) the numbers

/"¹ (j>j)XOR _Sj (resp. g'¹ (^)XOR _Sj), j = 1,.. ., k .

Clearly, B and C learn the secret they want. This follows because y'_b = f(x'_b) and y_c = g(x_c). A does not learn anything about the choices, and neither do B and C learn anything about each other's choices, since they know only their own one-way function. Attempts to choose more than one secret fail with an over­whelming probability because of Step 5, provided the number of bits in the s's is not very small.

In another simple protocol for secret selling of secrets A and B both use an own cryptosystem. The systems may be classical but they should be chosen from a collection, where the individual encryptions and decryptions commute.

Step 1: B gives A random bit sequences y_l, . . .,y_k (of the same length as the secrets s₍).

Step 2: A gives B the bit sequences z_} = E_A(SjXORyj), j = 1, . . . , k.

Step 3: B, having chosen the i-th secret and knowing the order of the z's, gives A the bit sequence x = £_B(z,).

Step 4: A gives B the bit sequence D_A(x).

Step 5: B computes D_BD_A(x) = s,XORy„ from which he, knowing y_it learns s,.

A possible way of cheating for B is to choose some combination of z's instead of Zj in Step 3 and, thus, to try to learn something about several secrets. The possibilities of success depend on the encryption method E_A.

The following is a further modification of oblivious transfer, often referred to as combined oblivious transfer. A and B possess secrets a and b, respectively, and g is any previously chosen function. During the protocol, B computes g(a, b), while A has no idea what B has computed. In other words, A obliviously transfers a prescribed combination of her and B's secret to B.

Date: 2015-02-16; view: 797