
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Legal World
The most widely used and tested public-key cryptosystem was originally introduced by Rivest, Shamir and Adleman, and is now referred to as the RSA system. It is based on an amazingly simple number-theoretical (one could even say arithmetical) idea, and yet it has been able to resist all cryptanalytic attacks. The idea is a clever use of the fact that, while it is easy to multiply two large primes, it is extremely difficult to factorize their product. Thus, the product can be publicized and used as the encryption key. The primes themselves cannot be recovered from the product. On the other hand, the primes are needed for decryption. Thus, we have an excellent framework for a public-key cryptosystem. Moreover, the details can be explained very fast - that's why we called the system "amazingly simple".
This section deals with RSA from the point of view of legal users. We discuss system design, as well as encryption and decryption. Both aspects of usage, privacy and authentication, will also be presented. Section 4.2 is about some simple facts and precautionary measures one should be aware of in system design. The next two sections are concerned with the interconnection between RSA and factorization. Section 4.3 presents, for instance, primality tests. Section 4.4 discusses cryptanalysis without factorization, that is, breaking RSA via some information other than the primes p and q. In Section 4.5 we'll come to the role of partial information: if we are able to find out certain facts about the plaintext, we are able to break the whole RSA. This means that RSA is as secure as some of its parts. In some sense, all of Sections 4.2-4.5 focus on the interplay between legal and illegal worlds, that is, between the cryptosystem designer and the cryptanalyst. The final Section 4.6 presents some systems related to RSA - the presentation will continue in Chapter 5.
It should be emphasized already at this point that there is no formal proof whatsoever (i) that factorization is intractable or is intractable in the special case needed for RSA, and (ii) that factorization is needed for the cryptanalysis of RSA, that is, there is no cryptanalytic method avoiding factorization. There is lots of empirical evidence for both (i) and (ii).
We now present the details of RSA. Let p and q be two distinct large random primes (typically, having about 100 digits in their decimal representation). Denote
n = pq and (p(n) = (p- 1 )(q - 1)
(Here q> is the Euler function mentioned also in Section 3.5.) Choose a large random number d > 1 such that (d, <p(n)) = 1 and compute the number e, 1 < e < (p(n), satisfying the congruence
ed = 1 (mod cp(n)) .
The numbers n, e and d are referred to as the modulus, encryption and decryption exponents, respectively. The numbers n and e constitute the public encryption key, whereas the remaining items p, q, cp(n) and d form the secret trapdoor. Clearly, the trapdoor information does not consist of four independent items. For instance, the knowledge of p immediately reveals the remaining three items.
To encrypt, one raises the plaintext to the power e and reduces modulo n. To decrypt, one raises the cryptotext to the power d and reduces modulo n.
More specifically, we assume that the plaintext is encoded as a decimal number. (We can equally well use binary representation if we like.) The number is divided into blocks of suitable size. The blocks are encrypted separately. A suitable size of the blocks is the unique integer i satisfying the inequalities 101"1 < n < 10'. In some cases one may choose i — 1 as the block size or make sure that each block is less than n if uniqueness of decryption is important. For instance, in Example 4.1 below n = 2773, implying that the block size equals 4. The numbers 1000 + 2773j are encrypted as the same number, for 7 = 0, 1,2, 3. However, only the value j = 0 leads to a possible plaintext in Example 4.1.
If w is a plaintext block and c the corresponding cryptotext block, then encryption can be expressed in terms of the following equation
c = (vvc, mod/i).
We now show that decryption works as intended.
Lemma 4.1. For w and c defined as above, (*) w = cd (mod n) .
Hence, if decryption is unique, w = (cd, mod n).
Proof. By the choice of d, there is a positive integer j such that ed = j<p(n) + 1. Assume first that neither p nor q divides w. By Euler's Theorem (see Appendix B), _ j (mo(j„)? yielding wed~l = 1 (modn). Hence,
c4 = (we)d = w (mod n).
If exactly one of p and q, say p, divides w, then 1 = 1 (modq), yielding in succession
= 1 (mod q), w}v(n) = 1 (mod q), wed = w (mod q).
Since the last congruence is clearly valid also modulo p, we obtain (*) also in this case. If both p and q divide w, we clearly have wed = w (modn), from which (*) follows as before. □
Consider again n = 2773. If we choose the block size 4, it may happen that decryption does not lead back to the original plaintext w, for instance, when w = 3773.
We now discuss the cryptosystem design, that is, how the different items are generated. In general, when we say that a random number is chosen or that we select something randomly, then we are using a random number generator, for instance, a computer program generating a sequence of digits that possesses as many statistical properties of a random sequence as possible. We do not discuss here any details concerning random number generators. To select the two large random primes p and q, one chooses randomly an odd integer r of appropriate size (say 100 digits) and tests it for primality. Primality tests are described in Section 4.3. In case of a negative answer, r + 2 is tested, and so forth. By the prime number theorem, there are approximately
10loo/ln 10100 - 10"/ln 10"
100-digit primes. (Here In refers to the natural logarithm.) When this number is compared with the number (10100 - 10")/2 of all 100-digit odd integers, we see that the probability of success for an individual test is approximately .00868.
Once p and q have been chosen, candidates for d are tested by Euclid's algorithm. When d satisfies (d,q>(n)) = 1, the chain of equations obtained from Euclid's algorithm gives immediately also e.
An operation needed for both encryption and decryption is modular exponentiation, that is, computing (ar,mod«). This can be done much faster than by repeatedly multiplying a by itself. The method we are referring to is squaring. After each squaring reduction modulo n takes place. In this way numbers greater than n1 are never encountered.
More specifically, we consider the binary representation of r,
r=JdxJ2i, Xj = 0, 1; k = [log2 r] -I- 1 .
j = o
Provided we know all numbers
(*) (a2J,modn), 0 < j < k ,
(ar, mod n) can be computed by forming at most k — 1 products and reducing each product modulo n. Thus, it suffices to compute the numbers (*), which involves k modular squarings, and in addition at most k — 1 modular products. This means computing at most 2k — 1 products with both factors less than n and reducing the products modulo n. If r is large and cp(n) is known then r may be first reduced modulo cp(n).
For instance, to compute (783, mod 61), we note that 760 = 1 (mod 61). Hence, we may compute (72\ mod 61) as well.
By successive squarings, we obtain the powers of 7 where the exponent is a power of 2:
| j | 0 1 | |||
| I2' | 7 49 |
Since 23 = 10111, we obtain the desired result
(723, mod 61) = (16(22(49-7)), mod 61)= 17 .
Sometimes one is lucky and finds the result even much faster. This is significant especially if the available computing power is low. For instance, in computing (191239, mod 323) one observes first that
1914 = 1 (mod 323), yielding 191236 = 1 (mod 323).
Since (1913, mod 323) = 115, one concludes that 115 is the answer also to the original question.
We have already considered the modulus n = 2773, and will still return to it in Example 4.1. To compute (192017, mod 2773), we consider first the powers of 2 as exponents:
0 1
19202J 1920 1083 2683 2554 820 We conclude that
(192017, mod2773) = (1920-820, mod2773) = 2109 . Since 17"1 = 157 (mod 2668), we may still verify the result by computing similarly (2109157, mod 2773) = 1920.
Observe that 2773 = 47-59 and <p(2773) = 2668.
When we still present a fast stochastic algorithm for primality in Section 4.3, we may conclude that all computations needed in cryptosystem design, as well as in encryption and legal decryption, can be carried out in low polynomial time. Still, the legal operations are roughly 1000 times faster in DES than in RSA.
Example 4.1. We consider three illustrations with the modulus growing in size. All of them should be readable, although even the largest one is unrealistic for practical security.
Take first p = 5, q = 11, n = 55, q>(n) = 40, e = 7, d = 23. Now plaintexts are numbers in the closed interval [1, 54], Moreover, we want to exclude numbers whose greatest common divisor with 55 exceeds 1, that is, numbers divisible by 5 or 11. In general, if (w, n) > 1 for some plaintext w, then we could factorize n by computing the greatest common divisor of n and the encrypted version of w. Of course, in this example we can factorize n anyway. In general the probability of a plaintext having a common nontrivial factor with n is less than 1/p + \jq. So the probability is negligible for large p and q.
In the example at hand it is easy enough to write down a complete encryption table.
| Plaintext | Cryptotext | Plaintext | Cryptotext |
| table can be rearranged to form a complete decryption table. | |||
| Cryptotext | Plaintext | Cryptotext | Plaintext |
Cryptotext Plaintext Cryptotext Plaintext
| 18 19 21 24 26 27 |
| 26 18 2 39 21 12 19 31 48 |
| 41 38 42 4 46 28 47 54 |
The following important fact is clearly visible from this example. Public-key cryptography never works for small plaintext spaces. A cryptanalyst can construct already at the preprocessing stage a complete decryption table simply by encrypting all possible plaintexts and rearranging the resulting cryptotexts in a convenient alphabetic order.
As a second illustration, consider p = 47, q = 59, n = 2773, (p(n) = 2668, e = 17, d = 157. Now the plaintext, encoded as a sequence of decimal digits, is divided into blocks of four digits. As we saw above, this might lead to a small ambiguity in the decryption process. However, no ambiguities will arise if the original plaintext is written using the 26 letters of the English alphabet, in which case the largest 4-digit number will be 2626.
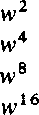
|
Let us make use of the additional dimension of security of a plaintext written in Finnish and encrypt the text SAUNOIN TAAS (I took a sauna bath again). The numerical encoding with the space getting the value 00 is as follows:
Plaintext block SA UN OI N- TA AS
Encoding 1901 2114 1509 1400 2001 0119
The modular exponentiations needed for encryption are carried out by squaring, as seen from the next table.
Plaintext w 1901 2114 1509 1400 2001 0119
582 1693 448 2262 2562 296
418 1740 1048 459 153 1653
25 2257 196 2706 1225 1004
| Cryptotext w |
625 48 2367 1716 432 1417
17 1281 1644 179 982 2029 2243
The result can be checked by raising similarly the cryptotext c to the power 157. For instance if c = 1644, we obtain
c2 = 1834, c4 = 2680, c8 = 330, c16 = 753, c32 = 1317, c64 = 1364, c128 = 2586, c144 = 612, c152 = 2304, c156 = 2022, c157 = 2114 .
For our final illustration, we consider the subsequent numbers. p = 3336670033 , q = 9876543211 , n = 32954765761773295963 , <p(n) = 32954765748560082720 , e = 1031 ,
d = 31963885304131991 .
The plaintext blocks will now consist of 20 digits. No ambiguities will be present if the plaintext blocks are obtained from English text by numerical encoding, which implies that all blocks begin with 0, 1 or 2.
Let us encrypt the following plaintext. "Sauna stoves are either preheated or continuously heated. Preheated means that the stove is not heated during the actual bathing. A smoke sauna is a special type of a preheated sauna. There is no chimney but smoke goes out through holes in the walls and roof."
Neither punctuation nor lower case letters are present in the encryption on the following page. We indicate also the block division and numerical encoding in the usual fashion.
After completing Example 4.1, we still return to some general matters. Also RSA can be viewed according to the general principles behind the construction of public-key cryptosystems, presented in Section 2.2. The setup is here not so clear as, for instance, in connection with knapsack-based cryptosystems. For a difficult problem P one may choose the factorization of n when n is known to be the product of two primes. An easy subproblem Peasy is P with the additional knowledge of <p(n). The shuffled version of Peasy is simply P itself. Or one may choose as the difficult problem P the solving of the congruence
xe = c (mod n)
when the triple (<?, c, n) consisting of RSA items is known. Peasy is in this case P with the additional knowledge of one of the items <p(n), d, p, q.
Both of the following points (i) and (ii) are rather obvious but have caused many misunderstandings, (i) There is no contradiction between the fact that the com- positeness of a given number n can be found out and the fact that n cannot be facorized. The former fact is needed in RSA system design, whereas the factorization of n would break the cryptosystem. Indeed, there are many results of the form "if n is prime then condition C(n) holds." Hence, if we observe that C(n) does not
| s | A | U | N | A | S | T | O | V | |||||||||||||||||||||
| E | S | A | R | E | E | I | T | ||||||||||||||||||||||
| H | E | R | P | R | E | H | E | A | |||||||||||||||||||||
| T | E | D | O | R | C | O | N | ||||||||||||||||||||||
| T | I | N | U | O | U | S | L | Y | |||||||||||||||||||||
| H | E | A | T | E | D | P | R | E | |||||||||||||||||||||
| H | E | A | T | E | D | M | E | A | |||||||||||||||||||||
| N | S | T | H | A | T | T | H | ||||||||||||||||||||||
| E | S | T | O | V | E | I | S | ||||||||||||||||||||||
| N | O | T | H | E | A | T | E | ||||||||||||||||||||||
| D | D | U | R | I | N | G | T | ||||||||||||||||||||||
| H | E | A | C | T | U | A | L | ||||||||||||||||||||||
| B | A | T | H | I | N | G | A | ||||||||||||||||||||||
| S | M | O | K | E | S | A | U | N | |||||||||||||||||||||
| A | I | S | A | S | P | E | |||||||||||||||||||||||
| C | I | A | L | T | Y | P | E | ||||||||||||||||||||||
| O | F | P | R | E | H | E | A | T | |||||||||||||||||||||
| E | D | S | A | U | N | A | T | ||||||||||||||||||||||
| H | E | R | E | I | S | N | O | ||||||||||||||||||||||
| C | H | I | M | N | E | Y | B | ||||||||||||||||||||||
| U | T | S | M | O | K | E | G | ||||||||||||||||||||||
| o | E | S | O | u | T | T | H | ||||||||||||||||||||||
| R | O | u | G | H | H | O | L | E | |||||||||||||||||||||
| S | I | N | T | H | E | W | |||||||||||||||||||||||
| A | L | L | S | A | N | D | R | ||||||||||||||||||||||
| O | O | F |
| Plaintext |
| Numerical Encoding |
| Cryptotext |
hold, we may conclude that n is composite but still cannot factorize n. (ii) For real-valued functions of real numbers, there is no difference, from the point of view of complexity, between exponentiation and computation of logarithms. In the discrete case modular exponentiation is easy, whereas logarithms constitute an intractable problem. This problem will be dealt with also in Section 4.6.
The problems of authentication and digital signatures were discussed already in Section 2.3. In what follows the subscripts indicate the user. Thus, eA, dA, nA are the encryption and decryption exponents and the modulus used by A. Assume first that only signature but not secrecy is needed in the transmission of messages. Then A sends the pair (w, DA(w)), where
Da(w) = (w\ modnj .
The receiver can verify the signature by applying /I's public encryption exponent eA. Since only A is in possession of dA, no other person could have signed the message w.
However, a forger can choose a number c, compute Ea{c) = (c'\ modnj
and claim successfully that c is the signature by A to the message Ea(c). This method of attack can be used for finding signatures to unpredictable messages only: only A can sign a prechosen message. Such unpredictable messages are not likely to be meaningful if, for instance, the plaintexts are obtained by numerical encoding from some natural language. Then the redundancy in the messages is high, and only a very small portion of blocks of a certain size are numerical encodings of parts of meaningful plaintext.
In addition to the amount of redundancy also the type of redundancy of plaintexts is important. In particular, neither the inverse of a meaningful message nor the product of two meaningful messages should be meaningful. Otherwise, a forger knowing /I's signatures s, to messages wt, i = 1,2, can sign, with the correct /4's signature, the messages (w, w2, mod nA) and (w i" 1, mod nA) using (s t s2, mod nA) and (si-1, modn^,).
Consider the first illustration in Example 4.1. The signatures for the messages 12 and 29 are 23 and 24, respectively. Clearly,
(12 • 29, mod 55) = 18 and (29"mod 55) = 19
can then be signed using
(23 • 24, mod 55) = 2 and (24" \ mod 55) = 39 .
Only nA and the signatures for w, are needed to construct the new signatures. This method of forging applies to products of more than two factors as well. Since apparently dA is always odd, we can sign also (— w,, mod nA) using (— s,, mod nA).
Assume, secondly, that both signature and secure transmission are requied. To send a signed message to B, A first signs it using (dA,nA) and then encrypts the result using (eB, nB). B first decrypts using the decryption exponent dB, after which the original message can be obtained using the public encyption key eA. The presence of dA in the message guarantees that it was sent by A. As before, one has to be cautious because of the possibility of forging signatures to unpredictable messages.
There is also another difficulty caused by the fact that A and B are using different moduli. Assume that nA > nB. Then DA(w) is not necessarily in the interval [1, riB — 1], and reduction modulo nB would certainly make the legal decryption more difficult. There are two ways to overcome this difficulty, (i) All users agree upon a common threshold t. Each user A chooses two RSA keys, one for signatures and the other for encryption. The items involved are denoted by superscripts s and e, respectively. Each user A takes care of that nsA < t < nA. The difficulty described above does not arise if A sends the message w to B in the form
EeB(DA(w)).
(ii) Also the threshold number can be avoided if messages from A to B are sent in the form EB(DA{w)) or DA(EB(w)), depending on whether nA < nB or nB < nA.
Date: 2015-02-16; view: 767
| <== previous page | | | next page ==> |
| Dense Knapsacks | | | Attack and Defense |