Structure of matter. Thermometry. Hooke’s law. Stress and Strain.

Young’s modulus. Force-separation and energy-separation curves.

Data: Young’s modulus for steel = 2.0 × 10¹¹ Pa; Young’s modulus for rubber = 5.0 × 10⁸ Pa

Acceleration due to free fall = 9.8 m s^-2; 1 atmosphere = 1.013 × 10⁵ Pa

density of water = 1000 kg m^-3

1) Explain briefly how liquids and gases differ in terms of their atoms and structure. (4 Marks)

2) Explain briefly in terms of atoms and with the help of a diagram(s) why solids expand when they are heated. (Your answer should not occupy more than half an A4 page). (8 Marks)

3) The interaction energy, U, between nearest neighbouring atoms in a long-chain molecule is given by:

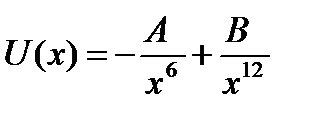
where A= 1.4 × 10^-77 J m⁶ and B = 1.0 × 10^-135 J m¹²

a) State, giving a reason, the resultant force between the two particles at their equilibrium separation. (2 Marks)

b) What is the equilibrium separation? (2 Marks)

4) A child throws a coin into the deep end of a swimming pool. The pool is 4 m deep. He then dives into the pool to retrieve the coin. Derive an equation for pressure as a function of depth, and plot P against depth to show what pressure is exerted on the boy as he swims downwards. Include the contribution of atmospheric pressure, whose average value at sea level is 1 atmosphere. (5 Marks)

5) Two open-ended barrels both have a radius of 25 cm. Three liquids have different densities: for A, ρ = 0.84 × 10³kg m^-3; for B, ρ = 0.92 × 10³kg m^-3and for C, ρ = 1.00 × 10³kg m^-3. Into the first barrel is poured 50 L of A, 50 L of B and 30 L of C. Into the second barrel is poured 40 L of A, 40 L of B and 50 L of C. Include atmospheric pressure in your calculations.

a) Explain briefly what happens to the different liquids after they have been poured into the barrels (note – the liquids are immiscible). (2 Marks)

b) What is the pressure at 35 cm above the bottom of the first barrel (3 Marks)

c) The content of the second barrel is poured into the first barrel. Whatnow is the pressure 35 cm above its bottom? (3 Marks)

6) The pressures recorded with a constant volume gas thermometer are 1.10 × 10⁵,

8.00 × 10⁴ and 8.51 × 10⁴ Pa at 100ºC, 0ºC and room temperature, respectively. What is the temperature at room temperature, in ºC and Kelvin? (3 Marks)

7) What force must be applied to a steel wire 6 m long, and diameter 1.6 mm to produce an extension of 1 mm? (3 Marks)

8). A muscle exerciser consists of two steel ropes attached to the end of a strong spring contained in a telescopic tube (see figure below). When the ropes are pulled sideways in opposite directions, the spring is compressed. The spring has an uncompressed length of 0.80 m. The force F required to compresses the spring to a length x is calculated from the equation F = 500(0.80-x) where F and x are measured in N and m respectively.

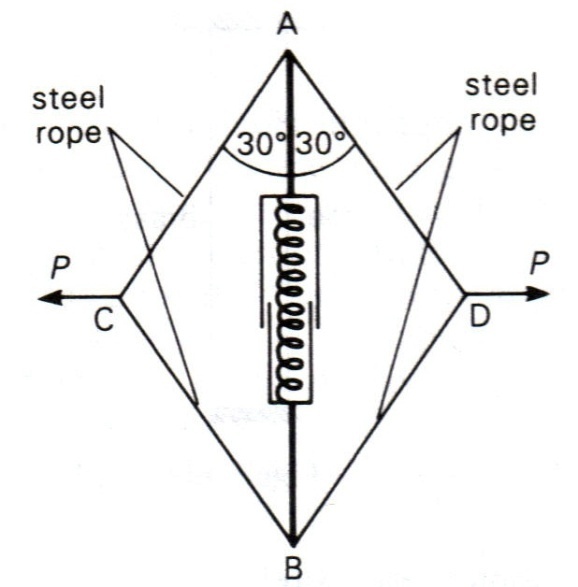
The ropes are pulled with equal and opposite forces, P, so that the spring is compressed to a length of 0.60 m and the ropes make an angle of 30º with the length of the spring.

Calculate:

a) the force, F (2 Marks)

b) the work done in compressing the spring (2 Marks)

c) the tension in each rope (2 Marks)

d) the force, P. (2 Marks)

9) a) Explain with words: stress, strain, Young modulus and elastic limit. (8 Marks)

b) Derive an expression in terms of the tensile force and extension for the energy stored in a stretched rubber cord which obeys Hooke’s law. (2 Marks)

c) The rubber cord of a catapult has a cross-sectional area of 1.0 mm² and a total unstretched length 10.0 cm. It is stretched to 12.0 cm and then released to project a missile of mass 5.0 g. Calculate the velocity of projection and state any assumptions that you have made. (4 Marks)

10) A nylon climbing rope is 10 mm in diameter and 30 m long. When it supports a climber of mass 80 kg, it gets 1.0 m longer.

a) What is the Young modulus of nylon? (2 Marks)

b) Imagine a situation in which the climber falls the full length of rope. Discuss what would happen if the rope were made of materials with a Young modulusi) one-tenth that of nylon, and ii) ten times that of nylon (assuming other dimensions are unchanged).

(6 Marks)

11) Sketch stress-strain curves on the same axes for copper, steel, glass and rubber. List the four materials in increasing order of a) stiffness, b) brittleness. (8 Marks)

12) The graph below displays a load against extension plot for a metal wire of diameter 1.5 mm and original length 1.0 m. When the load reached the value at A the wire broke.

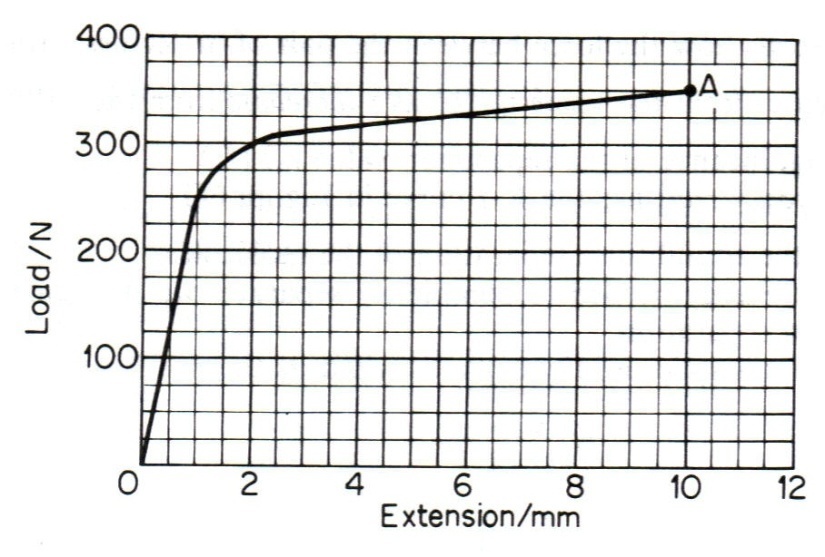
Using the graph, deduce values of:

a) the stress in the wire when it broke (2 Marks)

b) the work done in breaking the wire (2 Marks)

c) Young modulus for the metal of the wire. (2 Marks)

13) The figure shows a simplified view of a suspension bridge.

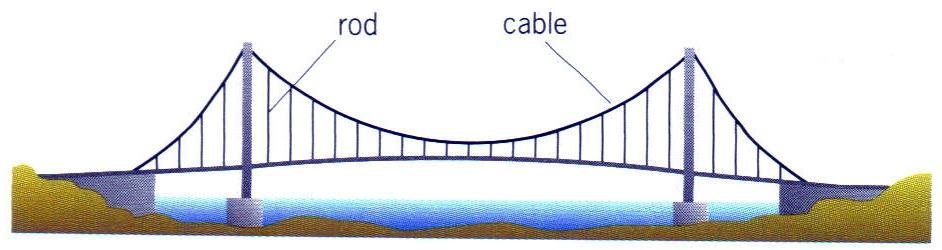
The road is supported by cylindrical steel rods attached to the suspension cables. There are two identical cables and sets of road on each side of the roadway. Each pair of rods effectively supports 5.0 m of road which has a mass perunit length of 2.0 × 10³ kg m^-1. The longest rods are 55 m long and have a cross-sectional area of 5.0 × 10^-3 m².

Assuming that the limit of proportionality is not exceeded, calculate:

i) the tension in each rod (2 Marks)

ii) the tensile stress in the longest rods, (2 Marks)

iii) the tensile strain in the longest rods, (2 Marks)

Date: 2015-02-03; view: 2394