
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
CHAPTER 9. Contracts 131 2 page
At the most basic level, this kind of decision problem can be modeled as a coordination game. Suppose that there are two choices of currency: gold or silver. At the beginning of a period, each person must decide which currency to carry (we assume that carrying both is too costly). During the period, each person meets various other people in the society at random, and they can trade only if they are both carrying the same currency. Thus the decision problem at the beginning of the period is to choose the currency that one thinks will be chosen by a majority of the others.
Schematically, we can model this situation as follows. Let p1 be the proportion in the population choosing gold at time I, and let 1 — p1 be the proportion choosing silver. In period t + 1, some people reconsider what they are doing (or they die and are replaced by people who must make a new decision). For the sake of simplicity, suppose that exactly one person, drawn at random from the general population, reconsiders during each period. Assume that the properties of gold and silver make them equally desirable as currencies. (We shall relax this assumption in a moment.) Then our decisionmaker chooses gold if p1 > .5 and chooses silver if p' < .5. if pi _ ä we can assume that the decisionmaker continues to do whatever he was previously doing because of inertia."' All of this happens with high probability, say, 1 -e. But with probability ñ > 0 a person chooses gold or silver at random, that is, for reasons external to the model.
Qualitatively, this process evolves in the following manner. After an 'nitial shakeout, the process converges quite rapidly to a situation in w 'ch most people are carrying the same currency—say, gold. This norm will very likely stay in place for a considerable period of time.
Eventually, however, an accumulation of random shocks will "tip" the process into the silver norm. These tipping incidents are infrequent compared to the periods in which one or the other norm is in place (assuming e is small). Moreover, once a tipping incident occurs, the process will tend to adjust quite rapidly to the new norm. This pattern—long periods of stasis punctuated by sudden changes of regime—is known in biology as the punctuated equilibrium effect. The evolutionary model we have described above predicts that a similar phenomenon characterizes shifts in economic and social norms. Figure 1.4 illustrates this phenomenon for the currency game when the two currencies have equal payoffs.
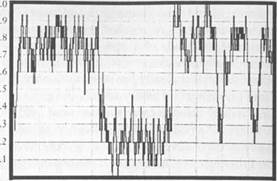
|
| Proportion Playing Gold |
| Time |
| Figure 1.4. The currency game with equal payoffs, population size 10, and e = .5. |
Now let us ask what happens when one currency is inherently a little better than the other. Suppose that gold is somewhat preferred because it does not tarnish as easily as silver. Then the decision problem at the individual level is to choose gold if p' > y, and to choose silver if p1 < y, where ó is some fraction less than .5 but larger than 0. Now the process follows a path that looks like Figure 1.5. Over the long run, there is a bias toward gold; that is, at any given time, the society is more likely to have adopted the gold standard than to have adopted the silver standard. This is not surprising. What is perhaps surprising is that the bias becomes larger the smaller the random perturbations are. Figures 1.6 and 1.7 show characteristic sample paths for s = .10 and e — .05. It is clear that the smaller the value of e, the more likely it is that the process is in a gold standard phase, and the longer are the
periods between shifts of regime. This can be verified analytically by computing the long-run distribution explicitly as a function of e, y, and the population size, as we show in Section 4.5.
A similar argument can be applied to a variety of other phenomena. Consider, for example, a competition between new technologies that have a networking effect. A contemporary example is personal computers: if most people own IBMs, it is advantageous to own an IBM; if most people own Macs, it is more desirable to own a Mac. The reason is that the more popular a given model is, the more software will be created for it, and the easier it will be to share programs with others.6
 Time
Figure 1.5. The currency game with asymmetric payoffs (gold = 3, silver = 2), population size 10, and e — .5.
Time
Figure 1.5. The currency game with asymmetric payoffs (gold = 3, silver = 2), population size 10, and e — .5.
|
| Proportion Playing Gold |
This situation can be modeled dynamically as follows. Imagine that there are m potential customers for two competing technologies. For the sake of concreteness, we shall stick with the case of personal computers. In each period, one person decides to buy a new computer. In the start-up phase, he may be a first-time buyer; in later phases, he will be replacing a computer he already owns. Suppose first that IBMs and Macs are equally desirable from the standpoint of operation and cost; the only thing that differentiates them is their current popularity. As in the currency game, there is a high probability that the customer will choose the more popular computer and a low probability that he will oose the other. Or, to be more realistic, we can suppose that the customer samples from the current population of users in order to estimate e one that is most popular, and then makes her choice. (This "par-
 30,000
Time
Figure 1.6. The currency game with asymmetric payoffs, population size 10, and r = .10.
30,000
Time
Figure 1.6. The currency game with asymmetric payoffs, population size 10, and r = .10.
|
tial information" model has long-run properties very similar to those of the full information model, as we shall show in later chapters.) Just as in the currency game, the process oscillates between periods in which first one technology and then the other is dominant. However, if one technology is better (even a little better) than the other, the model predicts that over the long run the process will find its way to the superior technology, which will tend to stay in place for longer periods of time than will the inferior one. In our terminology, the superior technology is stochastically stable.
This result must be interpreted with some caution, however, because the long run in such a model can be very long indeed compared to the rate of technological change. By the time the process finds its way to the superior technology, the nature of the two technologies may have changed entirely. As Arthur (1989) has argued, what matters from a practical standpoint is who seizes the largest share of the market initially, for this confers an advantage on the leader that can be very difficult to overcome in the short or intermediate run. To put it another way, if an inherently inferior technology gets a head start on an inherently superior one as a result of chance events, and if there are strong networking effects, then the inferior technology is likely to hold onto its lead for a long period of time before stochastic forces displace it in favor of the superior technology/

| Figure 1.7. The currency game with asymmetric payoffs, population size 10, and f = .05. |
| 60,000 |
| Time |
| 1.0 .9 .8 proportion Playing .6 Gold 5 .4 .3 .2 .1 0 |
Thus, from a short-run perspective, a key property of the system is its inertia, that is, the expected waiting time until the process tips from the less favorable to the more favorable regime. While this depends in part on the comparative superiority of one technology over the other, it also depends on (i) the size of the customer base, (ii) the amount of information on which customers base their decisions, (iii) the magnitude of the stochastic perturbations, and (iv) the extent to which customers gather information locally or globally. When people have a large information base and they interact globally, the inertia can be enormous: once an inferior technology gets a jump on a superior one, it can take almost forever for evolutionary forces to dislodge it. On the other hand, when people base their decisions on relatively little information, and they interact mainly with small groups of neighbors, the process can find its way to the optimum technology relatively quickly. Note, however, that low inertia is a two-edged sword: while it reduces the waiting time to get to the optimum outcome, the optimum does not remain in place as long before it risks being displaced (by further shocks) in favor of a suboptimal outcome.
This discussion raises an important issue in evolutionary models, namely, the time scale in which events unfold. In the processes we
tinct ^tUdy'time is measured in discrete periods that correspond to dis- events. For example, each interaction between a pair of individuals
might mark the beginning of a new period. When the population is large and people interact often, thousands or even millions of such events might be compressed within a short period of real time, such as an hour or a day. It is therefore not meaningful to make statements about short- versus long-run phenomena without a metric for translating event time into real time.
An implicit assumption in these models is that some parameters are changing much more slowly than others, so that the former can be viewed as fixed compared to the latter. When we model strategic behavior in a game, for example, we usually assume that the payoff structure remains fixed while the expectations of the players change. This assumption makes more sense in some cases than in others. In the competition between computer technologies, for example, payoffs may be changing so quickly that they need to be viewed as a dynamic element of the system. In other situations, the game may evolve very slowly. Consider the problem of which side of the road to drive on. At the micro level, this can be viewed as a game between two oncoming vehicles: both drivers want to coordinate on the same convention—left side or right side—in order to avoid an accident. Whether the game is played between horse-drawn carriages or high-speed automobiles, it is essentially a coordination game whose payoff structure does not change much over time. (Of course, the absolute payoffs change—the disutility of an accident increases as vehicles become faster—but all that matters is that the two competing conventions have equal payoffs.)
Rules of the road would therefore seem to be a good vehicle for studying the long-run properties of convention formation. Moreover, the history of left-right driving conventions in Europe exhibits the qualitative patterns that an evolutionary model would predict.8 In the early stages, when there was relatively little traffic on the roads and its range was limited, conventions grew up locally: a city or province would have one convention, while a few miles down the road another jurisdiction would have the opposite one. As use of the roads increased and people traveled further afield, these local rules tended to congeal first into regional and then into national norms, though for the most part these norms were not codified as traffic laws until well into the nineteenth century. In areas with highly fragmented jurisdictions, the congealing process took longer, as an evolutionary model would predict. Italy, for example, was characterized by highly localized left-right driving rules until well into the twentieth century.
Once conventions become established at the national level, the interactions are between countries, who are influenced by their neighbors: if enough of them follow the same convention, it pays to follow suit. Over time, we would expect a single convention to sweep across the board. While this intuition is essentially correct, it ignores the effect of idiosyncratic shocks, which can displace one convention in favor of another. Remarkably, just such a shock occurred in the history of European driving: the French Revolution. Up to that time, it was customary for carriages in France as well as in many other parts of Europe to keep to the left when passing. This meant that pedestrians often walked on the right to face the oncoming traffic. Keeping to the left was therefore associated with the privileged classes, while keeping to the right was considered more "democratic." Following the French Revolution, the convention was changed for symbolic reasons. Subsequently Napoleon adopted the new custom for his armies, and it spread to some of the countries he occupied.
From this point forward, one can see a gradual but steady shift— moving more or less from west to east—in favor of the right-hand rule. For example, Portugal, whose only border was with right-driving Spain, converted after World War I. Austria switched province by province, beginning with Vorarlberg and Tyrol in the west and ending with Vienna in the east, which held out until the Anschluss with Germany in 1938. Hungary and Czechoslovakia also converted under duress at about this time. The last continental European country to change from left to right was Sweden in 1967. Thus we see a dynamic response to an exogenous shock (the French Revolution) that played out over the course of almost two hundred years.
Of course, whether people drive on the left or the right is not particularly consequential in terms of social welfare. What matters is that society have an established convention in which expectations and behaviors are in equilibrium. It should be borne in mind, however, that some equilibria may be quite undesirable from the standpoint of social welfare. Indeed, some games are perverse in the sense that everyone does poorly in equilibrium. (Prisoner's dilemma is a prominent example.) Evolutionary arguments do not negate this problem; they
«n explain how bad equilibria come about, but they do not eliminate them.
Consider, for example, a situation in which two individuals cooperate to produce a joint product. They can either work hard or shirk. If both work, their output is high; if both shirk, their output is low. If one works and the other shirks, the output is the same as if both had shirked, but the one who worked put in more effort (in vain) and hence is less well off than the one who shirked.4 Assuming equal division of the spoils, we have a game with the following payoff structure (the specific numbers are unimportant):
| 10,10 | 0,7 |
| 7,0 | 7,7 |
| Work Shirk |
| Work Shirk |
If you expect your partner to work, it pays to work too; if you expect your partner to shirk, it is better to shirk. Thus two different norms can emerge: work or shirk. It turns out that in an evolutionary model of the type described above, shirking is stochastically stable: it is more likely to be the norm at any given time than working. The intuitive reason is that there is always some random variation in people's strategies, and hence some uncertainty about what one's partner will do. In such an environment, shirking is a safer strategy than working. Suppose, for example, that one believes that there is a greater than 30 percent chance that one's partner will shirk. Then it is best to shirk, too. On the other hand, one must believe that there is a greater than 70 percent chance that one's partner will work to make one want to work. In the terminology of Harsanyi and Selten (1988) the shirk norm is risk dominant.
But why would one believe that there is a 30 percent chance that one's partner is going to shirk when almost everyone is currently working? The answer has to do with variability in the population. Even if most people currently work hard, there will almost always be a few people who for some reason or other choose to shirk. Now suppose that someone outside this group of shirkers happens to interact with them for several periods. (This is particularly likely to happen if the shirkers are concentrated in some neighborhood.) This person will come to believe (given his or her limited information) that a sizable fraction of people shirk, which will induce him or her to shirk, too. This action will then be noticed by other people, which will further reinforce the idea that people are shirking. Shirking spreads by contagion. Of course, the process can also go in the reverse direction, whereby the work norm spreads by contagion. The point about the 30 percent-70 percent comparison is that it takes longer for accumulated variations to reach the 70 percent
I Id than to reach the 30 percent threshold, so the waiting time to ' ffrom shirk to work is longer than the other way around.
general, the inertia of the system—the waiting time needed to tip from one norm to another—depends in a fairly complex way on the Ï of the population, the extent to which people interact with their ^ • ,hbors or with those far away, the amount of the information they "ather, and so forth. This issue is explored in more detail in Chapters 4- 6 where we show that under a wide variety of conditions, the risk- dominant norm in a 2 x 2 game is stochastically stable. Over the long run, it has the evolutionary advantage whether or not the outcome is socially optimal. However, while stochastic stability and risk dominance usually coincide in 2 x 2 interactions, they are not the same thing in general, as we show in Chapter 7.
Stochastic evolutionary models are able to make quantitative predictions about the evolution of norms and institutions (sometimes surprisingly sharp ones), but their greatest significance lies in their qualitative properties. They have a different "look" and "feel" than equilibrium models. These qualitative features are sufficiently distinctive, in fact, that there is a reasonable prospect that they could be tested against empirical data. Although this task is well beyond the scope of the present book, we can suggest several features that, in principle, are testable.
To illustrate, consider a collection of distinct societies whose members do not interact with one another. Over time, each will develop distinctive institutions to cope with various types of economic and social coordination (forms of contracts, work norms, conventions of social behavior, and the like). We can think of these institutions as particular equilibrium outcomes in a game that has many (potential) equilibria. At any given time, a given society is likely to be "near equilibrium" in the sense that almost everybody follows the behavioral pattern that is expected of them and almost everybody wants to follow this behavior given the behavior they expect of others. Note that we say almost instead of all: there will inevitably be some misfits and nonconformists who do not follow established patterns. Moreover, according to the eory, these mutant types play a crucial role in promoting long-run c ange: occasionally they become numerous enough to tip society from one near-equilibrium to another. In particular, different societies may be hisT d'fferent eclu''ibria at any given point in time due to the vagaries of s ory. This fact has two general implications. On the one hand, it says iors T° Pe°ple in similar roles are more likely to exhibit similar behav- rS they corne from the same society than if they come from different societies, assuming all other explanatory variables are held constant. This is the local conformity effect. On the other hand, because the same process of adaptation is operating simultaneously in all of the societies, the frequency distribution of institutional forms will be fairly stable and predictable over the long run. In particular, the theory predicts that some institutions are inherently more stable or durable than others in the presence of stochastic shocks. Once established, they tend to persist for longer periods of time. Over the long run, these institutions will occur with higher frequency among the various villages. When the stochastic shocks are small, the mode of this frequency distribution will tend to be close to the stochastically stable institutions predicted by theory.
These two effects can in principle be identified from cross-sectional data. A third qualitative prediction, however, concerns the look of the evolutionary path and will only be revealed by time series data. The process will tend to exhibit long periods of stasis in which it is close to some equilibrium, punctuated by relatively brief periods in which the equilibrium shifts in response to stochastic shocks. We call this the punctuated equilibrium effect.10 It is a well-known feature of residential segregation patterns, but also occurs in other contexts and on different time scales. The spread of right-side driving in continental Europe appears to be one example where the tipping process took two centuries to run its course. Residential patterns, by contrast, often tip in a few years.
Organization of the Book
The book's argument is organized as follows. Chapter 2 discusses various models of adaptive behavior at the individual level. These include replicator dynamics, reinforcement models from psychology, imitation, and best-reply dynamics. For the sake of expositional clarity, we choose to focus on best-reply models, although a similar analysis could be carried out for other classes of adaptive rules. This choice is also governed by the fact that best-reply models have a firm foundation in the theory of individual choice. We can therefore address a variety of issues that are beyond the scope of the other frameworks, including the effects of risk aversion and amount of information on the evolutionary selection process.
The adaptive model is an elaboration of the feedback loop described above. Players develop expectations about others' behavior based on
eclent___ on information about what other people have done in the
ðÃåà This information is typically fragmentary and incomplete, be- PaSt i ^jven person will generally know only a small proportion of ^^relevant precedents, which he learns through his social network. Furthermore memory is bounded: players do not know (or perhaps do not care) about things that happened long ago; only recent events matter On the basis of her information, a player forms a simple statistical model of how others are likely to behave. Usually she chooses a best re ply given these expectations, but sometimes she makes arbitrary or unexplained choices. This simple model of adaptive behavior forms the basis of all the subsequent analysis.
In Chapter 3 we develop a conceptual framework for studying stochastic models of learning and adaptation more generally. The chapter opens with a discussion of asymptotic stability in deterministic dynamical systems, which is the standard concept in much of the evolutionary games literature. It is argued that this concept is not satisfactory as a predictor of long-run behavior when the system is subjected to persistent stochastic shocks (as almost all such systems are). The key concept of stochastic stability is introduced (Foster and Young, 1990). Loosely speaking, the stochastically stable states of an ergodic stochastic process are those states that occur with nonnegligible probability when the size of the stochastic perturbations is arbitrarily small. We develop a general framework for computing the stochastically stable states of any process that is Markovian, has stationary transition probabilities, and operates on a finite state space. The approach is illustrated with the neighborhood segregation model.
Chapter 4 applies this technique to the study of two-person coordination games in which each player has just two strategies. In this case, the stochastically stable outcome coincides with Harsanyi and Selten's concept of risk dominance. We explore the implications of this result for a variety of examples, including the currency game, the work-shirk game, and games of social etiquette. We then show how to compute the long-run distribution explicitly as a function of the population size and the error rate. This analysis shows that the selective bias in favor of e nsk-dominant equilibrium is quite marked even when the stochastic Perturbations are large, provided the population of players is also large.
n Chapter 5 we consider various refinements and embellishments of le^s learnin§ model- First, we examine the effects of having more or baS . ÎÃòà^ÎÏ/ *hat is, whether having a large or a small information Se ,s ad vantageous in the long run. It turns out that the answer is complex, and that having more information is an advantage in some kinds of games, but not in others. Then we show how to analyze situations where the populations are heterogeneous with respect to the individual payoff functions and the amount of information the players have. Next, we investigate the sensitivity of the selection results to different ways of modeling stochastic perturbations. In particular, we consider the case where players deviate from best reply at different rates. We also consider the possibility that they choose a nonbest reply with a probability that decreases as the prospective loss of payoff increases (Blume, 1993). Under either modification, the stochastically stable outcome in a symmetric 2x2 coordination game remains the risk-dominant equilibrium, just as in the case of uniform random errors.
Finally, we examine the situation where memory is not bounded, and players attach equal importance to all precedents no matter how dated they are. This process exhibits substantially different long-run behavior than does the process with bounded memory. In particular it is not ergodic: the process converges to an equilibrium (or near-equilibrium) regime with a probability that depends on the initial state. We argue, however, that this result is of mainly theoretical interest, since in practice past actions do not carry the same weight as recent ones.
Chapter 6 analyzes situations where players are located in a geographic or social space, and interact only with their "neighbors."11 We posit a perturbed best-reply process in which each player chooses an action with a probability that decreases exponentially the lower its expected payoff is, given what his neighbors are doing. This formulation allows us to represent the long-run probability of different states as a Gibbs distribution. Once again, we find that the stochastically stable outcome in a symmetric 2x2 game occurs when everyone plays the risk-dominant equilibrium. This framework is also convenient for studying the inertia of the system—how long it takes (in expectation) for the process to reach the stochastically stable outcome from an arbitrary initial state. Extending previous work of Ellison (1993), we show that the inertia of a local interaction system can be dramatically lower than the inertia of a system in which everyone interacts with everyone else. In particular, if everyone interacts with a sufficiently small, close-knit group, the inertia of the process is bounded above independently of the total population size.
In Chapter 7, we extend the analysis to arbitrary finite í-person games. Here the key concept for studying the long-run selection process is sets of strategies that are closed under best replies. Specifically, a curb set
Cartesian product set of strategies that includes all best replies to 1 ssjble probability mixtures over strategies in the set (Basu and yVeibull 1991)- A minimal curb set is one that contains no smaller curb j Building on work of Hurkens (1995), we show that in a generic Ü£ erson game, adaptive learning selects a minimal curb set; that is, in almost all è-person games there is a unique minimal curb set whose strategies are stochastically stable. We describe the general method for computing this set. In some classes of games the minimal curb sets correspond one to one with the strict Nash equilibria, in which case the learning model yields a theory of equilibrium selection. Moreover, there are important cases where theequilibria selected in these low-rationality environments are the same as those that emerge in the high-rationality world of classical theory.
Chapter 8 considers one such example, the Nash bargaining solution. In the traditional noncooperative model of bargaining, two players take turns making offers about how to divide a pie between themselves (Stahl, 1972; Rubinstein, 1982). If a player refuses an offer, the other player makes a counteroffer. If a player accepts an offer, the game ends. Assuming there is a small probability that the bargaining will "break down" after each refusal, the subgame perfect equilibrium outcome of this game is close to the division that maximizes the product of the players' utilities (the Nash bargaining solution). Note that this argument relies on the assumption that both players understand the structure of the game, that their utility functions are common knowledge, and that their rationality is common knowledge.
Date: 2016-04-22; view: 914
| <== previous page | | | next page ==> |
| CHAPTER 9. Contracts 131 1 page | | | CHAPTER 9. Contracts 131 4 page |