
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Using formula (4), we obtain
y¢õ=5u4 ·(–sin x).
Coming back to our "old" variable, we obtain y¢õ=-5 cos4x sinx.
Table of Principal Derived Functions



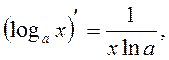
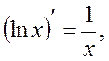
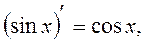
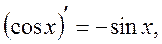
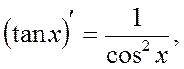
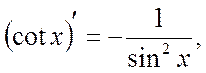
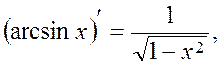


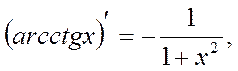
Differentiation of the Function Given Parametrically
Suppose that there is function y(õ) given parametrically:
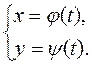
Suppose that functions j(t) and y(t) are differentiable in parameter t and j¢t¹0, there is also the inverse function t=t-1(x). Then the derivative of function can be obtained by the formula:
 . (6)
. (6)
Examples. 1. Find the derivative:

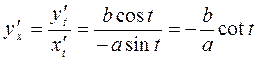 .
.
2. Find the derivative:

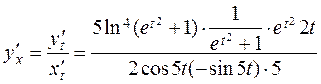 .
.
Method of Logarithmic Differentiation
The conception of this method is the following: beforehand, we obtain the logarithm of the assigned function, and only then differentiate the result.
In applications more often we encounter with two cases with the logarithmic differentiation.
1. Find the derivative of the product of several functions
y=u1(õ.)· u2.(õ)· u3.(õ)· …·un(õ).
Let us obtain the logarithm of both parts, using the property of the logarithm of product
ln y = ln u1.+ ln u2 + ln u3 +…+ ln un.
Differentiate both parts, the left one - as the implicit function
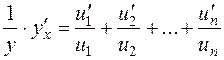 .
.
Multiplying both parts by ó and substituting it by the function itself, we obtain
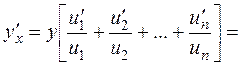 u1(õ). u2.(õ) ….un(õ)
u1(õ). u2.(õ) ….un(õ)  .
.
Example 1. Find the variable
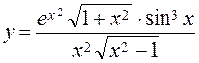 .
.
Find the logarithm of both parts
 .
.
Differentiate both parts
 .
.
Then, we obtain the required derivative
 .
.
Then out of this, we obtain the required derivative
 .
.
2. Consider the function
y=u(x)v(x),
here the base u(x) and v(x) the power are functions; thus, the function is called a power-exponential function.
Obtain the derivative of this function. By the analogy with the first case, obtain the logarithm and use the property of the logarithm of power
ln y = v(x). ln u(x).
Differentiate both parts
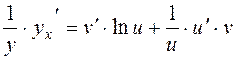 ,
,
multiplying both parts by ó and substituting by the power-exponential function; thus, we obtain the derivative
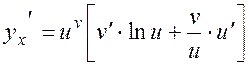 . (7)
. (7)
Example 2. Find the derivative
y=xx , ln y = x.ln x,
 .
.
Thus, the required derivtive is
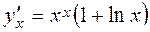 .
.
Differential of Function
Suppose that there is the differentiable function y=f(x) on the interval [a;b]. It follows that
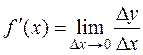 .
.
Acodrding to the principal theorem on limits, we have
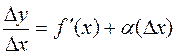 ,
, 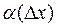 ®0 as Dõ®0 .
®0 as Dõ®0 .
Find the increment
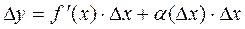 . (*)
. (*)
Definition. The principal part of the increment of function (*) is called a differential of function and is denoted by
 .
.
Find the differential of function ó=õ by definition
 or
or 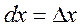 ,
,
i.e., the differential of the independent variable equals the increment of this variable. Substituting increment Dõ by dõ in the ratio, we obtain
 . (8)
. (8)
The differential of function equals the derivative of this function, multiplied by the differential of argument.
For example, y = cos2x, dy = –2 cos x·sin x·dx.
As the differential is the derivative multiplied by the differential of argument, then the differential of function has absolutely all properties, which the derivatives have, i.e.,
d(u±v) = du±dv,
d(u·v) = vdu+udv,
 .
.
Higher Derivatives
Suppose that there is the differentiable function y=f(x), i.e., there is the derivative y¢=f¢(x), which is denoted by f1(x) .
Definition. The derivative of the derivative of function is called the second derivative; the derivative of the second derivative of function is called the derivative of the third order respectively and is denoted by
 ,
,
 ,
,
. . . . . . .
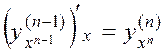
etc.
Notations:
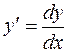 ,
,  , etc.,
, etc., 
are read, for example, the third derivative – d three y with respect to the third power of dx.
Date: 2015-01-02; view: 3279