
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Fundamental Theorems on Limits
Theorem I. The limit of the algebraic sum of finitely many functions equals the sum of the limits of these functions:
 .
.
Theorem II. The limit of the product of two functions equals the product of the limits of these functions:
 .
.
Theorem III. The limit of the ratio of two functions equals the quotient of the limits of the numerator and the denominator:
 .
.
Computations of limits. Examples.
I. Limits as x.
(1) 
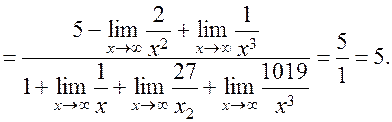
The limits in the numerator and the denominator equal zero.
To find the limit of a linear-fractional function, we must divide the numerator and the denominator by õ to the maximum power among the powers of x in the numerator and the denominator.
(2) 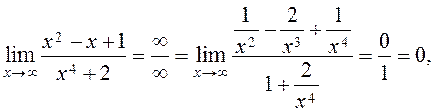
because õ4 is the maximum power of x in the numerator and the denominator.
(3) 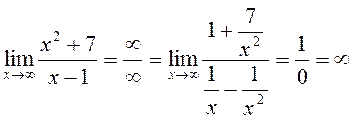 (divide by õ2).
(divide by õ2).
A simple method for finding limits of linear-fractional functions as õ is to leave the term containing the maximum power of õ in the numerator and the denominator:
4) 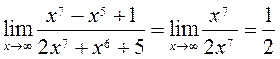 ,
,
5)  ,
,
6) 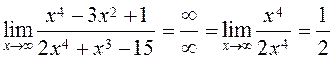 .
.
Let us find limits (1), (2), (3) by the simple method:
 ,
,
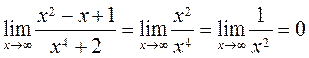 ,
,
 .
.
Deleting the terms containing lower powers of x from the numerator and the denominator is only possible because, after division by õ to the maximum power, the limits of all such terms vanish.
II. Limits as õà. Looking for a limit, first, substitute 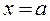 in the function. If we obtain a number, then this number is the limit of the function. If we obtain one of the indeterminacies
in the function. If we obtain a number, then this number is the limit of the function. If we obtain one of the indeterminacies 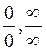 ,1, and
,1, and  , then we must eliminate it by transforming the function and then to pass to the limit.
, then we must eliminate it by transforming the function and then to pass to the limit.
(1)  ,
,
(2)  ,
,
(3) 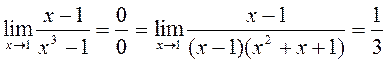 ,
,
The First Remarkable Limit and Its Generalization
The following limit exists and equals 1:
 .
.
Example:
(1)  ,
,
2) 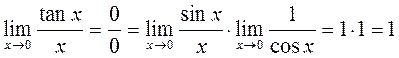 .
.
The first generalized remarkable limit. The first remarkable limit can be generalized, namely, written in the more general form
 (4)
(4)
In this formula, (õ) is an infinitesimal; it is very important that the argument of the sine and the denominator must be absolutely identical.
Examples.
(1) 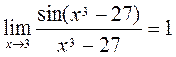 ,
,
(2) 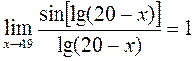 .
.
The Second Remarkable Limit
Consider the limit
 . (5)
. (5)
The number å satisfies the inequalities 2<e<3, e is an abbreviation for exponentials, i.e., «outer»; it is sometimes denoted by e=exp and approximately equals e2,71828. y=ex is the exponential function.
Examples. Find the following limits by using the second remarkable limit:
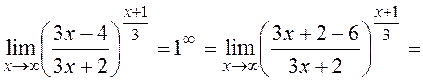
 .
.
The Second Generalized Remarkable Limit
The second remarkable limit (*) and its modification (**) can be generalized, i.e., written in the more general forms
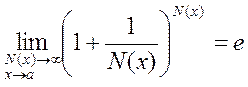
and
 . (6)
. (6)
In these formulas, (õ) is an infinitesimal and N(x) is an infinitude. It is very important that in these formulas, N(x) and (õ) are absolutely identical in the denominators and exponents.
For example,
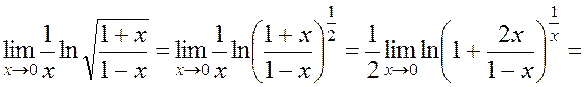

Other Remarkable Limits
Consider the following limits of functions often encountered in applications:
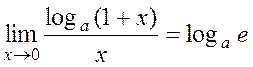 , (7)
, (7)
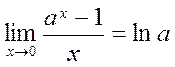 for a=e,
for a=e,  . (8)
. (8)
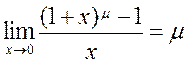 . (9)
. (9)
Date: 2015-01-02; view: 4723