Vector Product and Its Properties

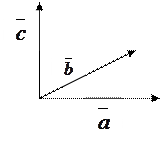Consider two vectors 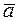and :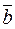

Definition. The vector product of two vectors 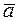and 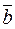is a vector , satisfying the following conditions:

(1) the absolute value of equals the product of the absolute values of the two given vectors and the sine of the angle between them:

; (*)

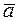(2) the vector is perpendicular to both vectors and :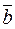

;

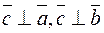(3) the three vectors 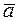, 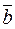and constitute a right triple of vectors (that is, looking from the tail of, we see that the shorter rotation from 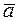to 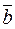is carried out anticlockwise). The vector product of 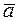and 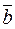is denoted by

.

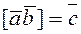1.The absolute value of the vector product of two vectors is equal to the area of the parallelogram spanned by these vectors:

.

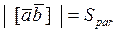2. The vector product is anticommutative, i.e.,

.

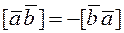3. To multiply a vector product by a number l, it is suffices to multiply one of the vectors by this number (without proof):

.

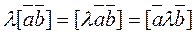4. Vector product is associative:

.

5. The vector product of collinear vectors is equal to zero, and vice versa, if the vector product of two vectors is zero, then these vectors are collinear.

Date: 2015-01-02; view: 882