The direction of a vector. Let us find the angle between two vectors and .

Consider the inner product

.

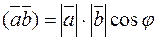We have

. (*)

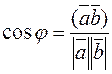Writing the product and absolute values in coordinates, we obtain

. (**)

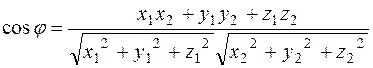Example 3. Find an angle between vectors 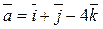and 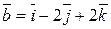. By using formula (**), we find

,

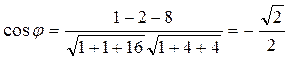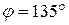
Let us determine a condition for vectors to be perpendicular. Suppose that vectors 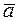and 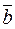are perpendicular, i.e., 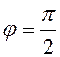; then 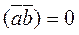, and

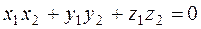. (7)

This is the condition for vectors to be perpendicular.

z

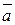
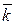
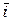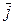0 y

x

Consider the angles between a vector 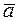and the unit vectors 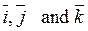. We denote these angles by

; ; .

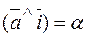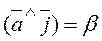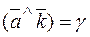Take the product of 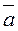and any unit vector, say, =

.

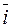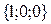
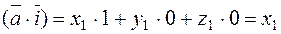By formula (*), the cosine of the angle a from it is

.

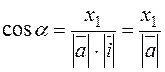Similarly the cosines of the other angles are

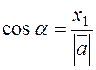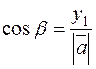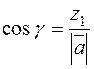, , . (8)

These cosines are called the directional cosines of the vector .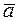

The sum of the squared directional cosines equals one:

.

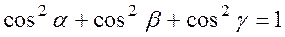To prove this, it sufficies to square the cosines by formula (8) and sum them:

.

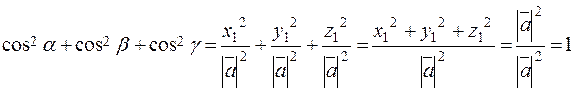Example 5. For what a are the vectors

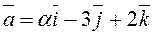and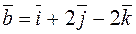

perpendicular?

We use the perpendicularity condition (7) and write the inner product of the given vectors in coordinates:

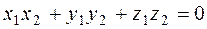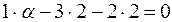; , a=10.

Date: 2015-01-02; view: 1636