VIII. RUPTURE IN PRESENCE OF FLUIDS

1. Effective pressure

Imagine a porous material made of grains, and (partly) bathed in a fluid (water for example). The fluid fraction may represent a few percents of the rock, up to more tha, 20% in sand. Excepted for the contacts between grains, which are responsible for the mechanical strength of the rock, at least in compression, all the grains are supposed to be wet such that the liquid forms a continuous phase thoughout the medium.

Such a wetted porous material is now subjected to a lithostatic pressure P_litho and the wetting fluid is subjected to a different pressure (usually P_fluid < P_litho ; Figure). These two pressures are isotropic. This situation is rather frequent in porous and permeable rocks since the rock density is larger than the density of the fluid (P_litho = r_rock gh, P_fluid = r_fluid gh , with r_rock > r_fluid ).

Contacts between grains transmit the lithostatic load to the material. However, since each grain is subjected to P_fluid , each grain, hence the whole material, is subjected to P_litho - P_fluid = P_eff, called effective pressure.

P_effective = P_litho – P_fluide

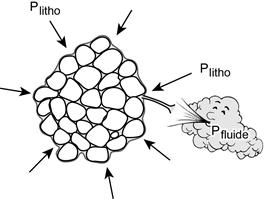
Figure. Fiction showing a porous medium subjected to both a lithostatic pressure and a fluid pressure. Viewed from the inside, each grain of the material is subjected to an effective pressure P_effectiv = P_litho – P_fluid.

Since s_{1 effective} = s₁ - P_fluid , and s_{3 effective} = s₃ - P_fluid , the consequence is: (s_{1 effective} + s_{3 effective}) / 2 = (s₁ + s₃) / 2 - P_fluid …

Therfore, after introduction of a fluid pressure, the centre of the Mohr circle is translated to the left-hand side by a magnitude P_fluid (Figure). We have just demonstrated that s_n is sensitive to the fluid pressure. Please demonstrate that the shear stress in independent of the fluid pressure. The Mohr circle (although translated° and keeps its initial diametre. This result has important consequences, particularly in civil ingeneering (dams …).

Note that in the « real life » it must be taken into account (at least at high confining pressures) of the incompressibility modules of the fluid fraction (K) and of the solid squeleton (K_s) under the form of the so-called Biot coefficient (b = 1- K/K_s) which tends to diminish the role of P_fluid since b <1 (K ≥ K_s). The effective pressure is not the exact difference between the solid and the fluid pressures.

Date: 2014-12-28; view: 1457