VII. THE GRIFFITH APPROACH

Alan Arnold Griffith (1893 -1963) was an English engineer, who, among many other contributions, is best known for his work on stress and fracture in metals that is now known as metal fatigue, as well as being one of the first to develop a strong theoretical basis for the jet engine !!.

1. Rupture in traction.

Griffith understood that rupture in tension is due to the catastrophic propagation of micro-defects that accumulate progressiveley in a material.

This approach stipulates that a number of randomly oriented defects (micro-fissures) already exist in a material (like for dislocations in a crystal …). Griffith analysed the stress distribution pattern around an elliptical defect (easier to model, with has b and l (b < l) as semi-axes) contained in an elastic and isotropic material (Figure) … and subjected to a maximum principal stress s₁ (horizontal in the figure for the sake of simplicity) and a vertical minimum stress (s₃).

Figure. Stress concentration at a fissure front.

At distance from the defect, the material is subjected to a differential stress (far stress-field) s = (s₁ - s₃). When approaching the defect, a stress concentration appears. At the tip of the defect (x = 0), the near stress-field is as follows (Figure):

s_max = s (1 + 2 l/b)

…. and decreases rapidly at distance from the defect (Figure).

In conclusion, the mechanism that tends to open the micro-defects is the tensile stress that accumulates at the tips (and very close to it). For a circular defect (l = b) s_max will be 3 times the applied differential stress. s_max will increase according to the inverse of the radius of curvature (r = b²/l) :

s_max / s = 1 + 2 (l/r)^1/2

The more acute is the defect (small radius of curvature) the higer s_max will be.

This explains why ancien people had a greater facility to built up Roman churches that Gothic ones ….

A fracture will appear after multiplication of such stress-induced fissures and their catastrophic propagation.

This approach allowed Griffith to calculate the relation between the shear stress and the normal stress in the tension domain (s_nc < 0) :

t_c² – 4Ts_nc- 4T² = 0

…. which is the equation of a parabola having the s_n axis as its axis of symmetry. The tangent of this parabola is parallel to the t axis at T (rupture in pure traction). The parabola intersects the t axis at C₀. It is indeed observed experimentally that (for materials whose elastic behaviour is directly related to the atomin bonds) C₀ ~ 2T (s_nc = 0 in the equation).

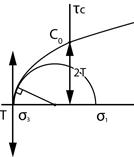
Figure. The Mohr envelop in traction (s_nc < 0) : the minimum principal stress is close to -T (2a ~ 0).

2. Rupture at high confinement environment

At low confining pressure the slope of the rupture envelop is rather high (it never exceeds 45°), indicating that, when the confining pressure (s_n) increases, the shear stress must increase accordingly … since the confining pressure tends to close the defects.

Beyond a certain magnitude of the confining pressure (hence a certain temperature … on Earth), the dislocations in the crystals tend to become active .. and the material becomes more able to deform plastically than to break. The friction decreases accordingly and the intrinsic curve flattens. Rupture may take place in the material after some plastic deformation … this is typical of the brittle-ductile transition.

In conclusion, the intrinsic curve of a material is hybrid, made of the Griffith parabola in the traction domain, the straight line of Coulomb in the low-pressure compressive domain, and made of a flat curve in the high-pressure compressive domain … leading to rupture planes tending to be at 45° with the maximum principal stress direction (2a 90°).

Date: 2014-12-28; view: 1313