
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Partial Information on RSA
The general question about partial information is very important in cryptography. Is it possible for the cryptanalyst to obtain some partial information about the plaintext, such as the last bit of the plaintext, although it might be intractable to get the whole plaintext? Sometimes such partial information might be crucially important.
There are many results for RSA to the effect that certain parts are as hard as the whole. In general, such results are of the following form. Suppose that we have an algorithm for obtaining about RSA certain partial cryptanalytic information, such as the last bit of the plaintext corresponding to an intercepted cryptotext. The algorithm is supposed to work in every instance of RSA cryptotexts. Then this algorithm can be converted, without too much increase in computational complexity, into a cryptanalytic algorithm that breaks RSA.
What this means is that, whenever RSA leaks such partial information, then the security can be entirely broken. If we trust that RSA cannot be broken, we can also be confident that no partial information of the kind dealt with in the results can be obtained. Of course, some partial information is always easily obtainable. For instance, if the last decimal digit of n is 3, then the last decimal digits of p and q are 1 and 3, or 7 and 9. Such partial information is not likely to disclose anything about the plaintext.
Are such results to the effect that certain parts are as hard as the whole a token of cryptographic strength or weakness? One can argue in both ways. If one has confidence in the system, security of the parts certainly adds to the confidence. When in doubt, the possibility of breaking the system by partial cryptanalysis makes the situation even more doubtful.
A convenient way to present results, where the existence of an algorithm is presupposed without giving any details of the algorithm, is to use an oracle. The
 Fig. 4.1
Fig. 4.1
|
oracle gives an answer to any question that the presupposed algorithm is able to settle, for instance, tells the last bit of a plaintext. The algorithm to be constructed, for instance, an algorithm for finding the whole plaintext, may during the computation ask questions of the proper form from the oracle. Such questions may be asked without any cost, that is, they do not affect the complexity. Thus, the complexity of the new algorithm depends on the "additional" steps only, and not of the complexity of the presupposed algorithm. If the latter is known, it is easy to estimate the complexity of the new algorithm, where the oracle is replaced by steps of the presupposed algorithm. The use of oracles is depicted in Fig. 4.1.
We begin with a simple illustration showing how an algorithm telling whether or not a plaintext x is less than n/2 can be used to obtain more information about x. Thus, we have at our disposal the following oracle 0 (size):
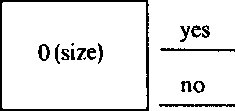 Fig. 4.2
Fig. 4.2
|
| if x < n/2, ifx > n/2. |
e, n, (xe, mod n)
This means that, given an input consisting of a public encryption key and the encrypted version of x, O(size) tells whether or not x < n/2.
We now construct an algorithm A telling in which of the intervals (/'n/8, {j + l)n/8) 0 <j <7, the plaintext x lies. Given the input consisting of e, n and (xe, mod n), the algorithm only has to compute the numbers
(*) (2exe, modn) and (4exe, modn),
and ask three questions from the oracle. Hence, the increase in complexity from any algorithm doing the job of O(size) to the algorithm A is negligible.
The three questions asked from the oracle are the one depicted in Fig. 4.2, and the questions where x6 is replaced by (2x)e and (4x)e. The latter two questions can be asked because the algorithm A has computed the numbers (*). The position of x depends on the answers to the three questions, posed in the order mentioned, according to the following table.
| Answers | Interval |
| yes, yes, yes | 0 < x < n/8 |
| yes, yes, no | n/8 < x < n/4 |
| yes, no, yes | n/4 < x < 3n/8 |
| yes, no, no | 3 n/8 < x < n/2 |
| no, yes, yes | n/2 < x < 5n/8 |
| no, yes, no | 5 n/8 < x < 3 n/4 |
| no, no, yes | 3 n/4 < x < 7 n/8 |
| no, no, no | 7n/8 < x < n |
It is easy to verify the results. For instance, assume that O(size) has given the information
x > n/2, (2x, mod n) < n/2, (4x, mod n) < n/2 ,
that is, the sequence of answers "no, yes, yes". The first two inequalities tell us that n/2 < x < 3n/4, because if x > 3n/4, then (2x, mod n) > n/2 and we would have "no" as the second answer. Combining this information with the last inequality, we obtain n/2 < x < 5n/8, because again 5n/8 < x < 3n/4 would imply (4x, modn) >'n/2.
This procedure can be carried out until the intervals become so small that x is uniquely determined by the interval to which it belongs. We will now present the details explicitly.
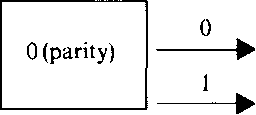
|
| if x is even, if x is odd. |
| Fig. 4.3 |
It will be convenient to use also the oracle O(parity) that will tell the parity of x. If we work with binary notation, O(parity) is naturally depicted as follows.
n, e, fx', mod n)
Thus, the oracle tells the last bit of x. We will now show how, using O(parity), x can be constructed bit by bit from the right.
Denote by N the number of bits in n (where 1 is the leading bit). Thus, N = [log2n] + 1. We also use the operators B and M producing from a number > 0 the corresponding binary sequence, and vice versa. For instance, B(91) = 1011011 and M(lOUOll) = 91. B(x) always begins with 1. The operators B and M are sometimes needed to avoid confusion.
For two sequences of bits, t and u, we denote by tu the sequence of bits obtained by writing t and u one after the other. The sequence tu is referred to as the catenation of t and u. As usual, we denote by |t| the length of the sequence t. If M(t)>M(u), we denote by LAST(f — u) the last |u| bits in the sequence B(M{t) - M(u)), where 0's are added to the beginning if\B(M{t) - M(u))\<\u\. In general, if LAST(/ - u) = v then | v | = | u | and, for some w, B(M(t) - M(u)) is a suffix of wv. For instance,
LAST(1011011 - 1010111) = 0000100 ,
LAST(1011011 - 111)= 100.
In the first case w is empty and, in the second case, w = 1010. The condition M(t) > M(u) guarantees that LAST(t - u) is always defined.
Let K be the inverse of 2e (mod n), that is,
2eK = 1 (modn)
The number K is found rapidly by Euclid's algorithm. Given (xe, mod n), we now define inductively r(i) and ANS(i'), for 1 <i<N.
By definition, r(I) = (xe, mod n) and ANS(l) is the answer given by O(parity) to the input x'. (We express the input in this short form because the items n and e remain unaltered during the discussion.) Assume that r(i — 1) and ANS(i — 1) have already been defined, for some i > 2. Then
. f (r(i — 1)K, mod n) if ANS(i - 1) = 0 , r(l) ~ j ((n - r(i - \))K, mod n) if ANS (» - 1) = 1 ,
and ANS(/) is the oracle's answer to the input /-(/')• Observe that it follows from the definition that r(i) is of the form (ye, mod «), for some y.
Secondly, we define t(i), N> i> 1, by descending induction. First,
t(N) = ANS(AT).
Assume that t(i), i > 2, has already been defined. Then
t(/)0 if ANS(i — 1) = 0 ,
| f(i- 1): |
LAST(B(n) - t(i)0) if ANS(; - 1) = 1 and M{t{i)0) < n LAST(t(i)0 - B(n)) if ANS(i - 1) = 1 and M(t(i)0) > n
Here the separation of ANS(i — 1) into two subcases is needed to guarantee that LAST is defined. In fact, the latter subcase occurs iff i = 2 and M(t(2)) > n/2. For instance, n = 21, B{n) = 10101 and t(2) = 1101.
As an example, take the first illustration in Example 4.1. We have n = 55, e = 7, N = 6 and B(n) = 110111. Euclid's algorithm gives K = 52. Assume that = 49. (We write instead of (xc, modn) for simplicity.) We obtain first
r(l) = 49 , ANS(l) = 0 ,
r(2) = 49-52 = 18, ANS(2) = 0 ,
r(3)= 18-52=1 , ANS(3) = 1 ,
r(4) = 54 • 52 = 3 , ANS(4) = 1 ,
r(5) = 52 • 52 = 9 , ANS(5) = 0 ,
r{6) = 9-52 = 28 , ANS(6) = 1 .
Of course, the values ANS(i) are not computed but obtained from the oracle. In this simple case they can be seen from the table given in Example 4.1.
Let us now compute the values t(i). The values t(6) = 1 and t(5) = 10 are immediate by the definition. Since ANS(4) = 1, we obtain
f(4) = LAST(110111 - 100) = 011 .
Similarly,
t(3) = LAST(110111 -0110) = 0001 .
The remaining values are again obtained by direct catenation: t(2) = 00010 and f(l) = 000100. It can now be immediately verified that r(l) is the binary representa
tion of x in N bits:
47 s 49 (mod 55).
This is true also in general.
Theorem 4.3. In the notation defined above,
M(t( 1)) = x .
Before proving Theorem 4.3, we observe that the oracle has to be consulted N times in order to find x. In addition, one application of Euclid's algorithm, as well as at most N - 1 modular multiplications and at most 2N subtractions are needed. Thus, the cryptanalytic algorithm for finding x is very fast if the oracle may be consulted without cost. In this sense a method for finding the last bit of the plaintext yields a method for finding the entire plaintext.
Proof of Theorem 4.3. For 1 < i < N, we denote by u(i) the number satisfying
u(i)e = r(i) (modn), 0 < u(i) < n .
Such numbers u(i) exist by the definition of r(i). More specifically, the relation 2er(i) = ± r(i - 1) (modn) shows how the numbers u(i) can be constructed successively. We denote also
v(i) = 0JB(u(i)),
where j = N — |B(u(i))l- Then j > 0 because u(i) < n. Thus, v{i) is always a binary sequence of length N.
We now claim that, for N > i > 1, there is a w(i'), possibly empty, such that
(*) v(i) = w(i)t(i).
Theorem 4.3 follows from (*) where we substitute i= 1. Observe first that |r(l)| = N because |f(N)| = 1 and the length increases by one in every transition from t(i) to t(i - 1). Since |u(l)| = N, (*) implies that w(l) must be empty and that u(l) and f(l) are the same binary sequence. On the other hand, M(y(l)) = x and, consequently, M(t(\)) = x.
Our claim (*) is established by descending induction on i. For i = N,{*) holds true because by definition the last bit of v(N) equals the last bit of B(u(N)) which, in turn, equals ANS(JV) = t(N). The inductive hypothesis is that (*) holds for the value /. Consider the value i — 1.
Assume first that ANS(i — 1) = 0. Then
r(i) = (r(i - 1 )K, modn)
and, consequently,
r(i - 1) = 2er(i) = (2u(i))e (modn),
which implies that «(/'- 1) = (2w(/), mod n). If B(u(i- 1)) = B{u{i))0 we obtain, by the inductive hypothesis and the definition of /(/'- 1),
v(i - 1) = w(i - l)f(i)0 = w(i - l)t(i - 1) and, therefore, (*) holds for the value i — 1 where w(i — 1) is obtained from w(i) by
omitting one 0 from the beginning. On the other hand, B(u(i — 1)) ^ B(u(i))0 implies that u(i — 1) = 2u{i) — n. (Clearly, 2u(i) < 2n.) Hence, u(i — 1) is odd, which contradicts the assumption ANS(i — 1) = 0. This shows that B(u{i - 1)) = B(u(i)) 0.
Assume, secondly, that ANS(i — 1) = 1. In this case
r(i - 1) = - 2er(i) = - 2eu(i)e = ( —2w(i))e (modn) .
Here the last congruence follows because e is odd. This implies that u(i — 1) = (— 2«(/'), modn). If n > 2u(i), then
v(i - 1) = w(i - l)LAST(B(n) - t(i)0) = w(i - l)t(i - 1).
If n < 2u(i), then
v(i - 1) = w(i - l)LAST(f(/)0 - B(n)) = w(» - l)t(i - 1).
The two alternatives correspond to the separation of ANS(/ — 1) = 1 into two subcases in the definition of t(i — 1).
This completes the inductive step and, consequently, (*) holds. □
The following Example 4.2 illustrates further various points in the above construction.
Example 4.2. Let us see first how u(i) and v(i) look like in the illustration given just before Theorem 4.3. Here again the table in Example 4.1 is useful. We obtain
u(6) — 7, v(6) = 000111 ,
u(5) = 14, y(5) = 001110 ,
u(4) = 27, y(4) = 011011 ,
k(3) = 1, i>(3) = 000001 ,
u(2) = 2, v(2) = 000010 ,
«(1) = 4, v(l) = 000100 .
Comparing the values v(i) and the previously computed values l(i), we infer that w(l) is empty and
w(2) = 0, w(3) = 00, w(4) = 011, w(5) = 0011, w(6) = 00011 .
As a second illustration, consider n = 57, e = 5, (xe, modn) = 48. We obtain first N = 6, B(n) = 111001, K = 41, and then the following values.
1 2 3 4 5 6
48 27 24 15 12 21
10 0 111
100001 01100 0110 011 11 1
33 12 6 3 27 15
| r(i) ANS(i) t(i) u(i) v(i) |
100001 001100 000110 000011 011011 001111
The next illustration is somewhat bigger. Consider n = 8137, e = 5X1, (xe, modn) = 5611. In this case we have N = 13, B{n) = 1111111001001,
25i7 = 2*12.32 = 6905-32 = 1261 (mod 8137),
whence K = 342. The resulting values of r(i), ANS(i) and t(i) are as follows.
| i | r(i) | ANS(i') | t(i) |
Consequently, x = A/(t(l)) = 16. The table can be filled in fast if the oracle can actually be consulted. However, because we do not have any oracle available, the values in the table have to be computed by some other method. Such a method cannot be tractable computationally or, otherwise, we are able to break RSA! In the computations above x = 16 was known a priori. Then the t- and ANS-columns can be computed top down. Once the ANS-column is known, the computation of the r-column is immediate. In this particular example we have
(p(n) = 7956 and d = 277 . □
Stronger results can be obtained for probabilistic algorithms. Given (xe, mod n), we are always able to guess the last bit of x with probability j- Suppose, however, that we have a slight advantage in guessing, that is, there is a positive e such that we are always able to guess the last bit of x with probability \ + e. Then we are able to break RSA. More explicitly, the following result is shown in [SchA]. Suppose the oracle 0(parity, e) tells the last bit of x with probability > \ + after receiving the input consisting of n, e and (xe, modn). If the oracle can be consulted without cost, there is a probabilistic polynomial time algorithm for computing x from the input mentioned. The algorithm is of Las Vegas type because the output can be checked by modular exponentiation.
We have considered an oracle telling the last bit of x. The result can be extended to concern oracles informing some other bit of x as well. In particular, the technique of Theorem 4.3 is almost directly applicable to the case, where the oracle tells the j'th bit from the end in B(x), and the binary representation of n ends with at least j I's. In Theorem 4.3 we have 7=1.
Instead of 0 (parity), we may as well use the oracle O(size) in considerations connected with Theorem 4.3. Indeed, for all z with 0 < z < n, we have z < «/2 iff (2z, mod n) is even. Because of this fact, each of the two oracles simulates the other.
Date: 2015-02-16; view: 834
| <== previous page | | | next page ==> |
| Primality | | | Discrete Logarithms and Key Exchange |