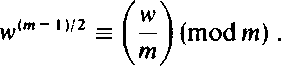Primality

This section presents some basic facts concerning primality and factoring, espe­cially from the point of view of RSA. For a more detailed discussion, the reader is referred to [Ko] and to the further references mentioned therein.

The problem PRIMALITY(n) was mentioned already in Section 2.2. An effi­cient algorithm for this problem is essential for RSA cryptosystem design. It is not known whether the problem is in P. However, this is not an essential drawback from the point of view of RSA because we have to construct primes of a certain size only and, moreover, stochastic algorithms with a low probability of failure are quite acceptable.

Such a stochastic algorithm works in most cases as follows. We consider a compositeness test C(m). If an integer m passes the test, it is definitely composite. If m fails the test, m may be a prime. The likelihood for m being prime increases with the number of compositeness tests it fails. Even if m passes a compositeness test, we still face the very difficult problem of factorizing m. As we have already emphasized, the security of RSA is based on the assumption that it is much easier to find two large primes p and q than it is to recover them if only their product n is known. This assumption is based on empirical evidence only; no theorem of this nature has been proved.

Since an RSA cryptosystem designer has to face the very unlikely possibility that the number p he has constructed is actually composite, let us investigate what such an error might actually mean. If p = p_i p₂, where p_t,p₂ as well as q are primes, then the designer works with a false (p_l(n) = (p — \)(q — 1), whereas the correct cp(n) = (p_l — 1 )(p₂ — l)(g — 1). Let u be the least common multiple of Pi ~ P2 ~ ' ^ancl 1 ~~ 1- Assume also that (w, n) = 1. Then the congruences

w"< ~¹ = 1 (mod p,), w^P2_1 = 1 (modp₂), w"'¹ = 1 (modq)

hold by Euler's Theorem and, consequently, w" = 1 is valid for all three moduli. This implies that

w" = 1 (mod n).

Clearly, u divides <p{n). If u divides also <p,(n), then

w^vM+1 = w(modn),

which means that encryption and decryption work as if p were prime. This happens, for instance, if the cryptosystem designer chooses p = 91, q = 41. Now

n = 3731, <p,(n) = 3600, q> (n) = 2880.

The least common multiple u of 6, 12 and 40 equals 120, a number dividing (p, («) = 3600. From this condition it also follows that whenever (d, cp _t («)) = 1, then also {d, (p(n)) = 1. Thus, one may compute e using the false (p_l without affecting the validity of D(E(w)) = w. Also no additional safety risks are introduced except that the least common multiple is considerably smaller than <p(n).

However, if u does not divide <p,(u), then in most cases D(E(w)) w, a fact likely to be noticed also by the cryptosystem designer. Assume that the numbers p = 391 and q = 281 are chosen without noticing that 391 = 17 - 23. Now the cryptosystem designer works with

n = 109871 and ^(w) = 109200 ,

whereas actually cp{n) = 98560. In this case u = 6160. Indeed, each of the numbers 16,22, 280 divides 6160. However, u does not divide (p_l(n), this being due to the fact that 11 divides u but does not divide </>,(")■ The cryptosystem designer might now choose d = 45979 and compute e = 19. For the plaintext w = 8 one obtains

_wed-I _{= 8}873600 = ₆₆g_{?9 (m0(}j _109871)

For the computation it is useful to observe that 8^{! 1} =70 (mod n) and keep in mind that 8⁶¹⁶⁰ = 1 (mod n).

Assume that m is an odd integer and (w, m) = 1. If m is prime then, by Euler's Theorem (also called in this case Fermat's Little Theorem),

(») w""-¹ = 1 (modm).

If m is not prime, it is possible but not likely that (*) holds. In such a case m is referred to as a pseudoprime to the base w.

This gives immediately the following compositeness test: m passes the test C(m) iff

(*)' w""¹ il(modm),

for some w with (w, m) = 1. If m fails the test C(m) for w, that is, (*) holds then m might still be composite.

Take the number m = 91 considered above. Then 2⁹⁰ = 2⁶⁴-2¹⁶-2⁸-2² = 16 • 16 • 74 • 4 = 64 (mod 91), which shows that 91 is composite. On the other hand, 3⁹⁰ = 1 (mod 91), which shows that 91 is a pseudoprime to the base 3. One can prove similarly that 341 is a pseudoprime to the base 2 and 217 is a pseudoprime to the base 5. In fact, one can also prove rather easily that the three numbers 341, 91 and 217 are the smallest pseudoprimes to the bases 2, 3 and 5, respectively.

Let us call an integer w with (w, m) - 1 and satisfying the congruence (*) a witness for the primality of m. As we have seen, there are also "false witnesses", to which m is a pseudoprime only. A method of showing with high probability that m is prime consists of gathering many witnesses for the primality of m. The next result provides some theoretical background.

Lemma 4.2. Either all or at most half of the integers w with 1 < w < m and (w, m) = 1 are witnesses for the primality of m.

Proof. Assume that w is not a witness (implying that (*)' holds). Let w_f, 1 < i < t, be all the witnesses. Then the numbers

Uj = (vvWj, mod m), 1 < i < t,

are all distinct and satisfy the conditions 1 < u_f < m and («,-, m) = 1. No number u_f can be a witness because

1 =u'i~^x=w^{m l}wf ¹ = w^m '(modm)

would contradict (*)'. There are as many numbers u_f as there are witnesses

altogether.

The probabilistic algorithm works as follows. Given m, choose a random w with 1 <w<m. The greatest common divisor (w, m) is found by Euclid's algorithm. If (w, m) > 1, we conclude that m is composite. Otherwise, we compute u = (w^m~ \ mod m) by repeated squaring. If u # 1, we conclude that m is composite. If u = 1, w is a witness for the primality of m, and we have some evidence that m could be prime. The more witnesses we find, the stronger the evidence will be. When we have found k witnesses, by Lemma 4.2 the probability of m being composite is at most 2~^k, except in the unfortunate case that all numbers w (with (w, m) = 1 and w < m) are witnesses. If m is prime then all numbers are witnesses, and the evidence obtained points toward the right conclusion. However, all numbers can be witnesses without m being prime. Such numbers m are referred to as Carmichael numbers. Thus, by definition, an odd composite number m is a Carmichael number iff (*) holds for all w with (w, m) = 1.

It is easy to prove that a Carmichael number is always square-free, and that an odd composite square-free number m is Carmichael number iff, whenever p is a prime dividing m, then also p — 1 divides m — 1. An immediate consequence of these facts is that a Carmichael number must be the product of at least three distinct primes. For instance, for m = 561 =3-11-17, each of the three numbers 3 — 1, 11 — 1 and 17—1 divides 561 — 1 and, consequently, 561 is a Carmichael number. In fact, it is the smallest Carmichael number.

Also 1729, 294409 and 56052361 are Carmichael numbers. They are all of the form (6i + 1) (12i + 1) (18i + 1), where the three factors are primes. (The three numbers are obtained for the values i = 1, 6, 35.) All numbers of this form, where the three factors are primes, are Carmichael numbers. There are also Carmichael numbers not of this form, for instance 2465 and 172081. It is not known whether there are infinitely many Carmichael numbers. The probability estimate 2~^k for the algorithm described above is not valid if the number m to be tested happens to be a Carmichael number. By this algorithm, our only chance to find out that m is composite is to hit a number w with (w, m) > 1 in our random choice of numbers w.

We now describe a test, referred to as the Solovay-Strassen primality test. It is very similar to the test described above, except that instead of(*) another condition (**) is used. No analogues of Carmichael number exist in connection with the latter condition. Thus, by finding more witnesses we always increase the probability that the tested number is a prime. The reader is referred to Appendix 5 for the definition

of the Legendre and Jacobi symbols

Lemma 4.3. If m is an odd prime then, for all w,

Proof. Clearly, (**) holds if m divides w. Otherwise, by Fermat's Little Theorem, (w^m~\ modm)= 1, yielding (w^<m_1)/2, modm) = ± 1 .

Let g be a generator of F*(m) (see Section 3.5), and let w = gK Then [ — ) = 1 iff

W

j is even iff (w^{(m 1)/2}, modm) = 1. Thus, both sides of (**) are congruent to +1, and are congruent to + 1 iff j is even. □

Odd composite numbers m satisfying (**), for some w with (w, m) = 1, are called Euler pseudoprimes to the base w. Because (**) implies (*), an Euler pseudoprime to the base w is also a pseudoprime to the base w. The converse is not true: 91 is a pseudoprime but not an Euler pseudoprime to the base 3 because (*) is satisfied but 3⁴⁵ = 27 (mod91), implying that (**) is not satisfied. 91 is an Euler pseudoprime to the base 10. The following lemma is analogous to Lemma 4.2 but deals with (**) instead of (*).

Lemma 4.4. If m is an odd composite number, then at most half of the integers w with 1 < w < m and (w, m) = 1 satisfy (**).

Proof. We first construct a w' such that (**) is not satisfied (for w = w'). Assume that the square p² of a prime p divides m. Then we choose w' = 1 + m/p. Now w'\

— =1 but the left side of (**) is not congruent to 1 (modm), since p does not m)

divide (m — l)/2.

Assume, secondly, that m is a product of distinct primes and p is one of them. Choose any quadratic nonresidue s modulo p and let w', 1 < w' < m, satisfy the congruences

w' = s (mod p), w' = 1 (mod m/p).

Such a w' is found by the Chinese Remainder Theorem. Then I — ) = — 1 but

\mj

_(w/)(m-i)/2 = j (_mod_m/p), yielding (w')^<m~^1)/2 # - 1 (modm) .

Having constructed a w' such that (**) is not satisfied, we let w_t, 1 < / < t, be all the integers satisfying (**) (as well as the usual conditions 1 < w_; < t, (w_t, m) = 1). Again the numbers

u_f = (w'w_f, mod m), 1 < i < t,

are all distinct and satisfy 1 < «, < m and (u_h m) = 1. If some u, satisfies (**), we obtain

_(H,')(m-i)/2 _wf-i_V2 _ (modm).

Since w, satisfies (**), we deduce further

(_w')<»-n/2 _ (modm),

contradicting the fact that w' does not satisfy (**). Hence, none of the numbers u_; satisfies (**). There are as many of them as there are numbers w_t. □

The Solovay-Strassen primality test uses (**) exactly in the same way as our earlier algorithm uses (*). To test the primality of m, we first choose a random number w < m. If (w, m) > 1, m is composite. Otherwise, we test the validity of(**).

fw\

This is easy from the point of view of complexity because the value of I — 1 can be

computed fast by the law of quadratic reciprocity. If (**) is not valid, m is composite. Otherwise, we regard w as a witness for the primality of m, choose another random number < m and repeat the procedure. After finding k witnesses, we may conclude by Lemmas 4.3 and 4.4 that the probability of m being composite is at most 2~*. The result is stronger than the one obtained for our previous algorithm because Lemma 4.4 shows that there are no analogues of Carmichael numbers when one works with (**). However, the estimate in Lemma 4.4 cannot be improved. There are numbers m which are Euler pseudoprimes to exactly half of all possible bases. Examples are the earlier mentioned Carmichael numbers 1729 and 56052361.

There is still another modification of the primality test, where the estimate in a lemma corresponding to Lemma 4.4 actually can be improved: at most 25% of the possible numbers are (false) witnesses for a composite number m to be prime. We now describe this test, known as the Miller-Rabin primality test. Some number- theoretic facts will be given without proofs-an interested reader is referred to [Ko]. The proofs are somewhat more complicated than in connection with the preceding tests.

Assume that m is a pseudoprime to the base w, that is, (*) holds. The idea is to extract successive square roots of the congruence (*) and check whether the first number # j _on the right side of the congruences thus obtained is actually equal to — 1. If m is prime, the first such number must equal to — 1 because then ± 1 are the only square roots modulo m. Thus we obtain another compositeness test. If m fails this test, that is, the first number different from 1 equals — 1, but m is composite, then m is referred to as a strong pseudoprime to the base w.

We now present the formal details. Assume that m is an odd composite number. Let 2^s be the highest power of 2 dividing m — 1, that is,

m — 1 = 2^sr, where r is odd .

Choose a number w with 1 < w < m and (w, m) = 1. Then m is a strong pseudoprime to the base w iff the following condition is satisfied:

(***) either w^r = 1 (modm) or w²'^r = — 1 (modm),

for some s' with 0 < s' < s.

Observe that the formal definition specifies the idea of extracting square roots of the congruence

w""¹ = w²'^r = 1 (modm) .

No further square roots can be extracted if w^r is reached on the left side.

It can be shown that a strong pseudoprime m to the base w is also an Euler pseudoprime to the base w. If m = 3 (mod 4) then also the converse holds true: in this case an Euler pseudoprime m to the base w is also a strong pseudoprime to the base w.

In the Miller-Rabin primality test we first compute m — 1 = 2^sr, where m is the given odd integer and r is odd. The random number w is chosen as before and the validity of (***) is tested. If the test fails, then m is composite. Otherwise, we regard w as a witness for the primality of m (in this case m is prime or a strong pseudoprime to the base w) and repeat the procedure for another w. Having found k witnesses for the primality of m, we may conclude that the probability of m being composite is at most 4~*. This is a consequence of the following lemma.

Lemma 4.5. If m is an odd composite integer, then m is a strong pseudoprime to the base w for at most 25% of all w's satisfying 1 < w < m.

It is not necessary to check through a large number of bases w in order to be almost sure that m is a prime if it is a strong pseudoprime to each of these bases. For instance, consider the four bases 2, 3, 5, 7. Only one composite number m < 2.5 • lO¹⁰, namely m = 3215031751, is a strong pseudoprime to each of these four bases.

Even a more general statement can be made, assuming that the "Generalized Riemann Hypothesis" is true. Under this assumption, if m is an odd composite integer then (***) fails to be true for at least one w < 2(lnm)². Thus it suffices to test numbers w up to this bound only. In this way the Miller-Rabin primality test is transformed into a deterministic algorithm that works in polynomial time. (The usual Riemann Hypothesis is the assertion that all complex zeros of the Riemann zeta-function, which lie on the "critical strip" (where the real part is between 0 and 1) actually lie on the "critical line" (where the real part equals i). The Generalized Riemann Hypothesis is the same assertion for generalizations of the zeta-function referred to as Dirichlet L-series.)

Assume that n is the modulus of RSA. If one is able to find a w such that n is a pseudoprime but not a strong pseudoprime to the base w then one is able to factorize n. This follows because in such a case one has found a number u # ± 1 (mod n) such that u² = 1 (mod n), which implies that (u + 1, n) is a nontrivial factor of n. A way to guard against this in the cryptosystem design is to make sure that p — 1 and q — 1 do not have a large common divisor.

We shall still return to matters dealing with (***) in Section 4.4.

Only the oldest and slowest primality test, the sieve of Eratosthenes, actually produces a prime factor of m at the same time it tells that m is composite. The sieve consists of testing the divisibility of m by prime numbers < sjm. All faster primality tests usually only tell that m is composite without saying anything about the factors.

Many factorization methods are known. We do not discuss them here, since none of them is feasible for the standard RSA with n having approximately 200 digits. So far the asymptotically fastest factorization algorithms are conjectured to run in time

where the constant a = 1 + s for s arbitrarily small. At the time of this writing, factorization of 100-digit numbers is computationally feasible.

4.4 Cryptanalysis and Factoring

We have already emphasized that there are no formal results to the effect that factoring n is actually needed in the cryptanalysis of RSA. It is conceivable that cryptanalysis can be carried out by entirely different means. However, if such other means disclose some of the secret trapdoor items, then they also lead to fast factoring of n. This will now be shown. The first result is very simple.

Lemma 4.6. Any algorithm for computing (p(n) is applicable, without increase in complexity, for factoring n.

Proof. The factor p can be immediately computed from the equations p + q = n - <p(n) + 1 and p - q = .J(p + q)² - 4n. □

Assume next that we have a method to compute the decryption exponent d. We want to show how this method can be used to factor n. The matter is not so straightforward as in Lemma 4.6. Moreover, the resulting factorization algorithm will be probabilistic. The probability of failure can be made arbitrarily small. The complexity of the new algorithm is not essentially higher than that of the algorithm for computing d. Of course the complexity of the new algorithm depends on the fixed probability but, for any probability, the new algorithm runs in polynomial time, provided the algorithm for computing d does so.

Theorem 4.1. An algorithm for computing d can be converted into a probabilistic algorithm for factoring n.

Proof. The proof is based on similar ideas as the discussion on pseudoprimes and strong pseudoprimes in Section 4.3. We present a proof independent of the latter discussion because of two reasons. Instead of a general m, we are dealing here with the special case of an RSA modulus n and, secondly, a reader might want to study Theorem 4.1 without going into primality tests.

In the proof we are using numbers w satisfying the conditions 1 < w < n and (w, n) = 1. These conditions are not repeated but should be kept in mind. It is clear that if a random choice of w < n satisfies (w, n) > 1 then we are immediately able to factor n. This holds true also if we have found a nontrivial square root of 1 (mod n), that is, a number u with the properties.

+ 1 (modn) and u² = 1 (modn).

Then (u + 1) (u — 1) is divisible by n but the factors are not and, consequently, (u + 1, n) equals either p or q. (This was observed already in Section 4.3.)

Since the given algorithm computes d, we can immediately obtain ed — 1 in the form

ed - 1 = 2^s r, s>l,rodd. Since ed — 1 is a multiple of <p(n), we obtain the congruence

w²'^r = 1 (modn)

for an arbitrary w. (Recall the additional conditions for w.) Consequently, for some s' with 0 < s' < s, s' is the smallest number such that the congruence

w²"^r = 1 (mod n)

is valid. If now

(*) s' > 0 and w²' '^r # - 1 (mod n),

we have found a nontrivial square root of 1 (mod n) and, therefore, completed the proof.

Assume that (*) is not satisfied, that is,

(*)' w^r = 1 (mod n) or w²'^r = — 1 (mod n), for some t, 0 < t < s .

Here the first congruence says that we have been able to reduce s' to 0 without encountering anything incongruent to 1 and, the second, that the value s' — 1 = t actually produces something congruent to —1.

We now determine an upper bound for the numbers w satisfying (*)'. Such numbers w are unwanted from the point of view of factorization whereas, as we already observed, numbers w satisfying (*) are wanted. Think of p — 1 and q — 1 written in the form

p — 1 = 2^la, q — 1 = 2^Jb, where a and b are odd .

We assume i < j without loss of generality. Since 2^sr is a multiple of (p(n), also r is a multiple of ab. Hence, if t > i then 2'r is a multiple of p — 1 and, consequently,

w²'^r = 1 (mod p).

From this we obtain further

w²'^r ^ — 1 (mod p), yielding w²'^r ^ — 1 (mod n).

This means that (*)' is never satisfied for t > i. Since clearly i < s, we may write (*)' in the equivalent form

(*)" w^r = 1 (modn) or w²'^r = — 1 (modn), for some t,0<t<i.

We now estimate the number of w's satisfying the first congruence in (*)". Let g be a generator of F*(p) and assume that w = g" (mod p). (It should be emphasized that in this proof we talk about numbers we are actually unable to compute. Such numbers are used only to justify the algorithm and do not appear in the execution.) Clearly, each of the congruences

w^r = 1 (mod p) and ur = 0 (mod p — 1)

implies the other. Hence, the congruences have the same number of solutions for the unknown w and u. The number of solutions for the latter congruence equals (r,p— 1) = a. Therefore, a is also the number of solutions for the former congruence.

Exactly in the same way we see that b is the number of solutions for the congruence w^r = 1 (mod q). This implies that ab is the number of solutions for the congruence w^r = 1 (mod n). (Note that every pair of solutions for the p- and ^-congruences yields a solution for the n-congruence by the Chinese Remainder Theorem. There are altogether ab such pairs.)

We estimate, secondly, the number of w's satisfying the second condition in (*)". Arguing exactly as before, we infer that the number of solutions w for the congruence

w²"'^r = 1 (modp) (resp. w²'^r = 1 (modp))

equals (2'⁺¹r,p - 1) = 2^{,+ l}a (resp. (2'r, p - 1) = 2'a). This follows because t + 1 < i. Consequently, the number of solutions for the congruence

w²'^r = — 1 (mod p)

is at most 2^{,+ i}a- 2'a = 2'a.

In the same way we conclude that the number of solutions for the congruence

w²'^r = — 1 (mod q)

is at most 2'b. (Here the inequality i < j is needed: t + 1 < i < j.) This implies that the number of solutions w for the congruence

w²'^r = — 1 (modn)

is at most 2'a-2'b = 2²'ab.

We are now ready to give an upper bound for the number of unwanted w's, that is, w's satisfying (*)' or, equivalently, (*)". Such an upper bound is obtained by adding the numbers of solutions for the first and second congruence in (*)", the latter number being the sum over the possible values of t:

ab + abY 2²' = ab(^l + 4'^ = ab(^\ +

= ab^2^i+J-¹ + ^(2 — 2^i+J~¹)^ < ab'2^i+J~^l = <p(n)/2 .

(Here the fact 1 <i<j has been used.) Since (p(n) is the number of all possible w's, at most 50% of all w's are unwanted. This means that, after testing k w's, the probability of not finding a wanted w is at most 2"*, converging rapidly to 0. □

In the argument above, we may consider also w's with (w, n) > 1 as wanted. Hence, the number of all possible w's is n - 1, of which <p(n)/2 is less than 50%. However, this improvement of the estimate is negligible, since w's with (w, n) > 1 are very rare exceptions. Assuming the generalized Riemann Hypothesis, one can show that there are very small wanted w's. This implies that Theorem 4.1 can be expressed, for instance, in the form: any deterministic polynomial-time algorithm for computing d can be converted into a deterministic polynomial-time algorithm for factoring n.

RSA is applicable also to an environment, where the moduli, as well as encryption and decryption exponents, are distributed by an agency which all parties involved trust. Assume that the agency publicizes a modulus n common to everybody, as well as the encryption exponents e_A, e_B,. . . of the users A, B,.... In addition, the agency distributes to the users individually the secret decryption exponents d_A,d_B,.... The primes p and q are known to the agency only. This setup is vulnerable in the sense of the following theorem. The method is similar to that of Theorem 4.1. The result can be viewed as an example of cryptanalysis without factoring n.

Theorem 4.2. In the setup described above any user is able to find in deterministic cubic time another user's secret decryption exponent (withoutfactoring n).

Proof. We show how B can find d_A. For some k,

e_Bd_B ~ 1 = k(p(n) .

B does not know k but knows e_B, d_B, e_A and n. Let t be some number dividing e_gd_B - 1 and satisfying

a = (e_Bd_B - 1 )/t, where (a, e_A) = 1 .

We cannot choose t = (e_Bd_B — 1, e_A) because, for instance, the square of a factor of e_A may divide e_Bd_B— 1. There is, however, a simple deterministic algorithm, running in cubic time, for computing / and a. In fact, denote

e_B^dB - 1 = 0o> (9o, e_A) = h₀ and define inductively, for i > 1,

9i = Qi-i/hi-u (g_i,e_A) = h_i.

For h = 1, we may choose t = h_ih₂... h.md a=g.. For h. > 2, we have ,</_i+ , <gJ 2. This means that h. = 1 is found in a linear number of steps. At each step, Euclid's algorithm is called, yielding altogether the cubic time estimate. B now computes by Euclid's algorithm a and b such that

aa. + be_A = 1 ,

where b is chosen to be positive. Observe that q>(n) divides a because a = k<p(n)/t, where k/t is an integer because (t, cp(n)) = 1. The latter equation follows because {e_A, q>{n)) = 1 and, hence, t is a product of numbers, none of which has a nontrivial factor common with <p(n). The observation implies the congruence

be_A = 1 (mod cp(n)),

and hence b (reduced modulo n) can be used as d_A. □

Although in Theorem 4.2 B constructs d_A without factoring n, Theorem 4.1 can then be used to factor n.

Date: 2015-02-16; view: 708