Work Done on a System by an External Force

In Chapter 7, we defined work as being energy transferred to or from an object by means of a force acting on the object. We can now extend that definition to an external force acting on a system of objects.

Work is energy transferred to or from a system by means of an external force acting on that system.

Figure 8-1 la represents positive work (a transfer of energy to a system), and Fig. 8-1 lb represents negative work (a transfer of energy from a system). When more than one force acts on a system, their net work is the energy transferred to or from the system.

These transfers are like transfers of money to and from a bank account. If a system consists of a single particle or particle-like object, as in Chapter 7, the work done on the system by a force can change only the kinetic energy of the system. The energy statement for such transfers is the work-kinetic energy theorem of Eq. 7-10 ( 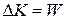); that is, a single particle has only one energy account, called kinetic energy. External forces can transfer energy into or out of that account. If a system is more complicated, however, an external force can change other forms of energy (such as potential energy); that is, a more complicated system can have multiple energy accounts.

Let us find energy statements for such systems by examining two basic situa­tions, one that does not involve friction and one that does.

No Friction Involved

To compete in a bowling-ball hurling contest, you first squat and cup your hands under the ball on the floor. Then you rapidly straighten up while also pulling your hands up sharply, launching the ball upward at about face level. During your upward motion, your applied force on the ball obviously does work; that is, it is an external force that transfers energy, but to what system?

To answer, we check to see which energies change. There is a change 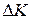in the ball's kinetic energy and, because the ball and Earth become more separated, there is a change in the gravitational potential energy of the ball-Earth system. To include both changes, we need to consider the ball-Earth system. Then your force is an external force doing work on that system, and the work is

, (8-23)

Or 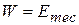(work done on system, no friction involved), (8-24)

where 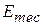is the change in the mechanical energy of the system. These two equations, which are represented in Fig. 8-12, are equivalent energy statements for work done on a system by an external force when friction is not involved.

Date: 2015-01-12; view: 1770