
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Work and Kinetic EnergyFinding an Expression for Work Let us find an expression for work by considering a bead that can slide along a frictionless wire, which is stretched along a horizontal where
Solving this equation for The first term on the left side of the equation is the kinetic energy
If we know values for To calculate the work done on an object by a force during a displacement, we use only the force component along the object's displacement. The force component perpendicular to the displacement does zero work. From Fig. 7-2, we see that we can write
This equation is useful for calculating the work if we know values for
(You may wish to review the discussion of scalar products in Section 3-7.) Equation 7-8 is especially useful for calculating the work when Cautions: There are two restrictions to using Eqs. 7-6 through 7-8 to calculate work done on an object by a force. First, the force must be a constant force; that is, it must not change in magnitude or direction as the object moves. (Later, we shall discuss what to do with a variable force that changes in magnitude.) Second, the object must be particle-like. This means that the object must be rigid; all parts of the object must move together, in the same direction. In this chapter we consider only particle-like objects, such as the bed and its rider being pushed in Fig. 7-3.
Fig. 7-5 A contestant in a bed race. We can approximate the bed and its rider as being a particle for the purpose of calculating the work done on them by the force applied by the student. Signs for work. The work done on an object by a force can be either positive work or negative work. For example, if the angle A force does positive work when it has a vector component in the same direction as the displacement, and it does negative work when it has a vector component in the opposite direction. It does zero work when it has no such vector component. Units for work. Work has the SI unit of the joule, the same as kinetic energy. However, from Eqs. 7-6 and 7-7 we can see that an equivalent unit is the newton-meter (N • m). The corresponding unit in the British system is the foot-pound (ft • lb). Extending Eq. 7-2, we have 1 J = kg • m2/s2 = 1 N • m = 0.738 ft • lb.(7-9) Net work done by several forces. When two or more forces act on an object, the net work done on the object is the sum of the works done by the individual forces. We can calculate the net work in two ways. (1) We can find the work done by each force and then sum those works. (2) Alternatively, we can first find the net force Work-Kinetic Energy Theorem Equation 7-5 relates the change in kinetic energy of the bead (from an initial
which says that
which says that
These statements are known traditionally as the work-kinetic energy theorem for particles. They hold for both positive and negative work: If the net work done on a particle is positive, then the particle's kinetic energy increases by the amount of the work. If the net work done is negative, then the particle's kinetic energy decreases by the amount of the work. For example, if the kinetic energy is initially 5 J and there is a net transfer of 2 J to the particle (positive net work), then the final kinetic energy is 7 J. If, instead, there is a net transfer of 2 J from the particle (negative net work), then the final kinetic energy is 3 J.
Fig. 7-6 A particle-like tomato of mass m thrown upward slows from velocity 70 to velocity ~v during displacement d because the gravitational force Fg acts on it. A kinetic energy gauge indicates the resulting change in the kinetic energy of the object, from ËÃ, (= {mv§) to Kf{= \mv2).
Date: 2015-01-12; view: 1437
|
 axis (Fig. 7-2). A constant force
axis (Fig. 7-2). A constant force  , directed at an angle
, directed at an angle 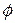 to the wire, accelerates the bead along the wire. We can relate the force and the acceleration with Newton's second law, written for components along the
to the wire, accelerates the bead along the wire. We can relate the force and the acceleration with Newton's second law, written for components along the 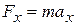 (7-3)
(7-3)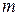 is the bead's mass. As the bead moves through a displacement
is the bead's mass. As the bead moves through a displacement 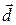 , the force changes the bead's velocity from an initial value
, the force changes the bead's velocity from an initial value 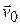 to another value
to another value 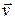 . Because the force is constant, we know that the acceleration is also constant. Thus, we can use Eq. 2-16 (one of the basic constant-acceleration equations of Chapter 2) to write, for components along the
. Because the force is constant, we know that the acceleration is also constant. Thus, we can use Eq. 2-16 (one of the basic constant-acceleration equations of Chapter 2) to write, for components along the 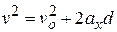 (7-4)
(7-4)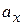 , substituting into Eq. 7-3, and rearranging then give us
, substituting into Eq. 7-3, and rearranging then give us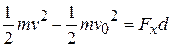 (7-5)
(7-5)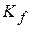 of the bead at the end of the displacement
of the bead at the end of the displacement  , and the second term is the kinetic energy
, and the second term is the kinetic energy 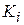 of the bead at the start of the displacement. Thus, the left side of Eq. 7-5 tells us the kinetic energy has been changed by the force, and the right side tells us the change is equal to
of the bead at the start of the displacement. Thus, the left side of Eq. 7-5 tells us the kinetic energy has been changed by the force, and the right side tells us the change is equal to  . Therefore, the work
. Therefore, the work 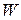 done on the bead by the force (the energy transfer due to the force) is
done on the bead by the force (the energy transfer due to the force) is . (7-6)
. (7-6)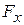 and
and 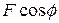 , where
, where 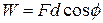 (work done by a constant force) (7-7)
(work done by a constant force) (7-7)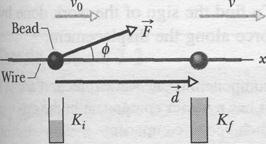 Fig. 7-2 A constant force F directed at angle ô to the displacement d of a bead on a wire accelerates the bead along the wire, changing the velocity of the bead from ~v0 to 7. A "kinetic energy gauge" indicates the resulting change in the kinetic energy of the bead, from the value Kt to Kf.
Fig. 7-2 A constant force F directed at angle ô to the displacement d of a bead on a wire accelerates the bead along the wire, changing the velocity of the bead from ~v0 to 7. A "kinetic energy gauge" indicates the resulting change in the kinetic energy of the bead, from the value Kt to Kf.
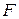 ,
,  , we can also write
, we can also write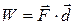 done by a constant force). (7-8)
done by a constant force). (7-8)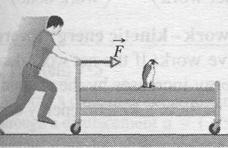
 is positive and thus so is the work. If
is positive and thus so is the work. If 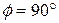 ?) These results lead to a simple rule. To find the sign of the work done by a force, consider the vector component of the force along the displacement:
?) These results lead to a simple rule. To find the sign of the work done by a force, consider the vector component of the force along the displacement: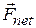 of those forces. Then we can use Eq. 7-7, substituting the magnitude
of those forces. Then we can use Eq. 7-7, substituting the magnitude 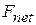 for
for 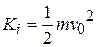 to a later
to a later 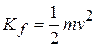 ) to the work
) to the work 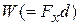 done on the bead. For such particle-like objects, we can generalize that equation. Let
done on the bead. For such particle-like objects, we can generalize that equation. Let 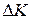 be the change in the kinetic energy of the object, and
be the change in the kinetic energy of the object, and 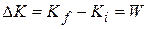 (7-10)
(7-10)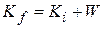 (7-11)
(7-11)