| Velocity and Coordinate by IntegrationWhen  varies with time, we can use the relation varies with time, we can use the relation 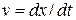 to find the velocity to find the velocity 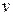 as a function of time if the position as a function of time if the position  is a given function of time. Similarly, we can use is a given function of time. Similarly, we can use 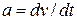 to find the acceleration to find the acceleration 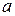 as a function of time if the velocity as a function of time if the velocity 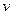 is a given function of time. is a given function of time.
We can also reverse this process. Suppose 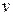 is known as a function of time; how can we find is known as a function of time; how can we find  as a function of time? To answer this question, we first as a function of time? To answer this question, we first
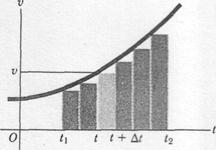 Fig.3 The area under a velocity-time graph equals the displacement
Fig.3 The area under a velocity-time graph equals the displacement
| consider a graphical approach. Figure 3 shows a velocity-versus-time curve for a situation where the acceleration (the slope of the curve) is not constant but increases with time. Considering the motion during the interval between times 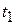 and and 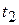 , we divide this total interval into many smaller intervals, calling a typical one , we divide this total interval into many smaller intervals, calling a typical one 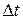 . Let the velocity during that interval be . Let the velocity during that interval be 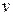 . Of course, the velocity changes during . Of course, the velocity changes during 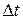 , but if the interval is very small, the change will also be very small. This displacement during that interval, neglecting the variation of , but if the interval is very small, the change will also be very small. This displacement during that interval, neglecting the variation of 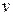 , is given by , is given by
 . .
This corresponds graphically to the area of the shaded strip with height 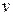 and width and width 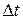 , that is, the area under the curve corresponding to the interval , that is, the area under the curve corresponding to the interval 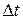 . Since the total displacement in any interval (say, . Since the total displacement in any interval (say, 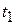 to to 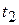 ) is the sum of the displacements in the small subintervals, the total displacement is given graphically by the total area under the curve between the vertical lines ) is the sum of the displacements in the small subintervals, the total displacement is given graphically by the total area under the curve between the vertical lines 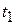 and and 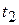 . In the limit, when all the . In the limit, when all the 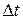 become very small and their number very large, this is simply the integral of become very small and their number very large, this is simply the integral of 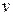 (which is in general a function of (which is in general a function of  ) from ) from 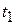 and and 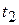 . Thus . Thus  is the position at time is the position at time 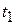 and and  the position at time the position at time 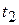 : :
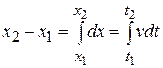 (2-14) (2-14)
A similar analysis with the acceleration-versus-time curve, where 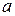 is in general a function of is in general a function of  , shows that if , shows that if  is the velocity at time is the velocity at time 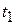 and and 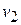 the velocity at time the velocity at time 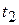 , the change in velocity , the change in velocity  during a small time interval during a small time interval 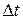 is approximately equal to is approximately equal to 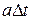 , and the total change in velocity ( , and the total change in velocity ( 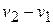 ) during the interval ) during the interval  is given by is given by
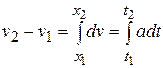
Or, finally, 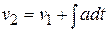 . .
Exercises
1. Velocity of a body, moving in viscous medium, is given by the equation  , where , where 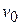 - initial velocity, - initial velocity, 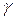 - constant. What are the distance and acceleration as function of time? - constant. What are the distance and acceleration as function of time?
2. A particle moves along a straight line with velocity 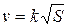 , where , where 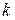 is constant. If at time is constant. If at time 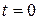 the distance, traveled the particle was the distance, traveled the particle was 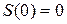 , determine: (a) dependence of speed and acceleration on time ( , determine: (a) dependence of speed and acceleration on time (  and and  ) )
3. (a) If particle’s acceleration is given by 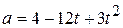 , (where , (where 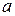 is in meter/second2 and is in meter/second2 and  in seconds), what its velocity at in seconds), what its velocity at 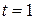 ? (b) What is its coordinate at ? (b) What is its coordinate at 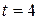 s? s?
Date: 2015-01-12; view: 1301
|

 varies with time, we can use the relation
varies with time, we can use the relation 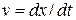 to find the velocity
to find the velocity 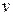 as a function of time if the position
as a function of time if the position 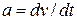 to find the acceleration
to find the acceleration 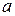 as a function of time if the velocity
as a function of time if the velocity 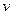 is a given function of time.
is a given function of time. Fig.3 The area under a velocity-time graph equals the displacement
Fig.3 The area under a velocity-time graph equals the displacement
 and
and 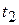 , we divide this total interval into many smaller intervals, calling a typical one
, we divide this total interval into many smaller intervals, calling a typical one 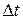 . Let the velocity during that interval be
. Let the velocity during that interval be  .
. ) from
) from  is the position at time
is the position at time  the position at time
the position at time 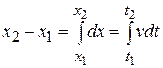 (2-14)
(2-14) is the velocity at time
is the velocity at time 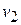 the velocity at time
the velocity at time  during a small time interval
during a small time interval 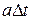 , and the total change in velocity (
, and the total change in velocity ( 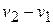 ) during the interval
) during the interval  is given by
is given by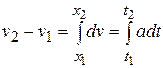
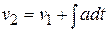 .
. , where
, where 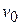 - initial velocity,
- initial velocity, 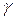 - constant. What are the distance and acceleration as function of time?
- constant. What are the distance and acceleration as function of time?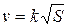 , where
, where 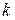 is constant. If at time
is constant. If at time 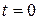 the distance, traveled the particle was
the distance, traveled the particle was 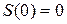 , determine: (a) dependence of speed and acceleration on time (
, determine: (a) dependence of speed and acceleration on time (  and
and  )
)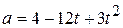 , (where
, (where 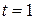 ? (b) What is its coordinate at
? (b) What is its coordinate at 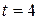 s?
s?